3.2. 浮點數

Go語言提供了兩種精度的浮點數，float32和float64。它們的算術規範由IEEE754浮點數國際標準定義，該浮點數規範被所有現代的CPU支持。

這些浮點數類型的取值範圍可以從很微小到很巨大。浮點數的範圍極限值可以在math包找到。常量math.MaxFloat32表示float32能表示的最大數值，大約是 3.4e38；對應的math.MaxFloat64常量大約是1.8e308。它們分別能表示的最小值近似為1.4e-45和4.9e-324。

一個float32類型的浮點數可以提供大約6個十進制數的精度，而float64則可以提供約15個十進制數的精度；通常應該優先使用float64類型，因為float32類型的累計計算誤差很容易擴散，並且float32能精確表示的正整數並不是很大（譯註：因為float32的有效bit位只有23個，其它的bit位用於指數和符號；當整數大於23bit能表達的範圍時，float32的表示將出現誤差）：

var f float32 = 16777216 // 1 << 24
fmt.Println(f == f+1)    // "true"!

浮點數的字面值可以直接寫小數部分，像這樣：

const e = 2.71828 // (approximately)

小數點前面或後面的數字都可能被省略（例如.707或1.）。很小或很大的數最好用科學計數法書寫，通過e或E來指定指數部分：

const Avogadro = 6.02214129e23  // 阿伏伽德羅常數
const Planck   = 6.62606957e-34 // 普朗克常數

用Printf函數的%g參數打印浮點數，將採用更緊湊的表示形式打印，並提供足夠的精度，但是對應表格的數據，使用%e（帶指數）或%f的形式打印可能更合適。所有的這三個打印形式都可以指定打印的寬度和控制打印精度。

for x := 0; x < 8; x++ {
    fmt.Printf("x = %d e^x = %8.3f\n", x, math.Exp(float64(x)))
}

上面代碼打印e的冪，打印精度是小數點後三個小數精度和8個字符寬度：

x = 0       e^x =    1.000
x = 1       e^x =    2.718
x = 2       e^x =    7.389
x = 3       e^x =   20.086
x = 4       e^x =   54.598
x = 5       e^x =  148.413
x = 6       e^x =  403.429
x = 7       e^x = 1096.633

math包中除了提供大量常用的數學函數外，還提供了IEEE754浮點數標準中定義的特殊值的創建和測試：正無窮大和負無窮大，分別用於表示太大溢出的數字和除零的結果；還有NaN非數，一般用於表示無效的除法操作結果0/0或Sqrt(-1).

var z float64
fmt.Println(z, -z, 1/z, -1/z, z/z) // "0 -0 +Inf -Inf NaN"

函數math.IsNaN用於測試一個數是否是非數NaN，math.NaN則返回非數對應的值。雖然可以用math.NaN來表示一個非法的結果，但是測試一個結果是否是非數NaN則是充滿風險的，因為NaN和任何數都是不相等的（譯註：在浮點數中，NaN、正無窮大和負無窮大都不是唯一的，每個都有非常多種的bit模式表示）：

nan := math.NaN()
fmt.Println(nan == nan, nan < nan, nan > nan) // "false false false"

如果一個函數返回的浮點數結果可能失敗，最好的做法是用單獨的標誌報告失敗，像這樣：

func compute() (value float64, ok bool) {
    // ...
    if failed {
        return 0, false
    }
    return result, true
}

接下來的程序演示了通過浮點計算生成的圖形。它是帶有兩個參數的z = f(x, y)函數的三維形式，使用了可縮放矢量圖形（SVG）格式輸出，SVG是一個用於矢量線繪製的XML標準。圖3.1顯示了sin(r)/r函數的輸出圖形，其中r是sqrt(x*x+y*y)。

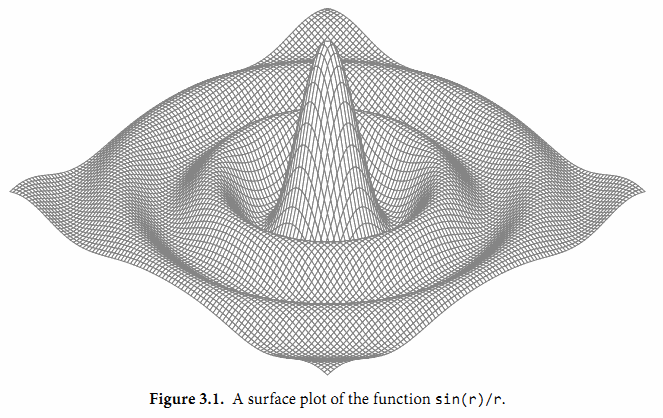
gopl.io/ch3/surface

// Surface computes an SVG rendering of a 3-D surface function.
package main

import (
    "fmt"
    "math"
)

const (
    width, height = 600, 320            // canvas size in pixels
    cells         = 100                 // number of grid cells
    xyrange       = 30.0                // axis ranges (-xyrange..+xyrange)
    xyscale       = width / 2 / xyrange // pixels per x or y unit
    zscale        = height * 0.4        // pixels per z unit
    angle         = math.Pi / 6         // angle of x, y axes (=30°)
)

var sin30, cos30 = math.Sin(angle), math.Cos(angle) // sin(30°), cos(30°)

func main() {
    fmt.Printf("<svg xmlns='http://www.w3.org/2000/svg' "+
        "style='stroke: grey; fill: white; stroke-width: 0.7' "+
        "width='%d' height='%d'>", width, height)
    for i := 0; i < cells; i++ {
        for j := 0; j < cells; j++ {
            ax, ay := corner(i+1, j)
            bx, by := corner(i, j)
            cx, cy := corner(i, j+1)
            dx, dy := corner(i+1, j+1)
            fmt.Printf("<polygon points='%g,%g %g,%g %g,%g %g,%g'/>\n",
                ax, ay, bx, by, cx, cy, dx, dy)
        }
    }
    fmt.Println("</svg>")
}

func corner(i, j int) (float64, float64) {
    // Find point (x,y) at corner of cell (i,j).
    x := xyrange * (float64(i)/cells - 0.5)
    y := xyrange * (float64(j)/cells - 0.5)

    // Compute surface height z.
    z := f(x, y)

    // Project (x,y,z) isometrically onto 2-D SVG canvas (sx,sy).
    sx := width/2 + (x-y)*cos30*xyscale
    sy := height/2 + (x+y)*sin30*xyscale - z*zscale
    return sx, sy
}

func f(x, y float64) float64 {
    r := math.Hypot(x, y) // distance from (0,0)
    return math.Sin(r) / r
}

要注意的是corner函數返回了兩個結果，分別對應每個網格頂點的座標參數。

要解釋這個程序是如何工作的需要一些基本的幾何學知識，但是我們可以跳過幾何學原理，因為程序的重點是演示浮點數運算。程序的本質是三個不同的座標系中映射關係，如圖3.2所示。第一個是100x100的二維網格，對應整數座標(i,j)，從遠處的(0,0)位置開始。我們從遠處向前面繪製，因此遠處先繪製的多邊形有可能被前面後繪製的多邊形覆蓋。

第二個座標系是一個三維的網格浮點座標(x,y,z)，其中x和y是i和j的線性函數，通過平移轉換為網格單元的中心，然後用xyrange係數縮放。高度z是函數f(x,y)的值。

第三個座標系是一個二維的畫布，起點(0,0)在左上角。畫布中點的座標用(sx,sy)表示。我們使用等角投影將三維點(x,y,z)投影到二維的畫布中。

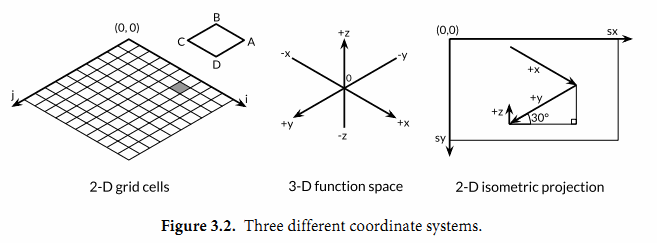
畫布中從遠處到右邊的點對應較大的x值和較大的y值。並且畫布中x和y值越大，則對應的z值越小。x和y的垂直和水平縮放係數來自30度角的正弦和餘弦值。z的縮放係數0.4，是一個任意選擇的參數。

對於二維網格中的每一個網格單元，main函數計算單元的四個頂點在畫布中對應多邊形ABCD的頂點，其中B對應(i,j)頂點位置，A、C和D是其它相鄰的頂點，然後輸出SVG的繪製指令。

練習 3.1： 如果f函數返回的是無限制的float64值，那麼SVG文件可能輸出無效的多邊形元素（雖然許多SVG渲染器會妥善處理這類問題）。修改程序跳過無效的多邊形。

練習 3.2： 試驗math包中其他函數的渲染圖形。你是否能輸出一個egg box、moguls或a saddle圖案?

練習 3.3： 根據高度給每個多邊形上色，那樣峰值部將是紅色（#ff0000），谷部將是藍色（#0000ff）。

練習 3.4： 參考1.7節Lissajous例子的函數，構造一個web服務器，用於計算函數曲面然後返回SVG數據給客戶端。服務器必須設置Content-Type頭部：

w.Header().Set("Content-Type", "image/svg+xml")

（這一步在Lissajous例子中不是必須的，因為服務器使用標準的PNG圖像格式，可以根據前面的512個字節自動輸出對應的頭部。）允許客戶端通過HTTP請求參數設置高度、寬度和顏色等參數。