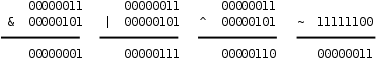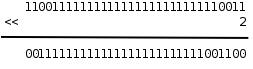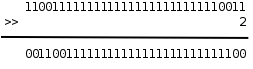整數在計算機中用二進制的位來表示,C語言提供一些運算符可以直接操作整數中的位,稱為位運算,這些運算符的操作數都必須是整型的。在以後的學習中你會發現,有些信息利用整數中的某幾個位來存儲,要訪問這些位,僅僅有對整數的操作是不夠的,必須借助位運算,例如第 2 節 “Unicode和UTF-8”介紹的UTF-8編碼就是如此,學完本節之後你應該能自己寫出UTF-8的編碼和解碼程序。本節首先介紹各種位運算符,然後介紹與位運算有關的編程技巧。
在第 3 節 “布爾代數”講過邏輯與、或、非運算,並列出了真值表,對於整數中的位也可以做與、或、非運算,C語言提供了按位與(Bitwise AND)運算符&、按位或(Bitwise OR)運算符|和按位取反(Bitwise NOT)運算符~,此外還有按位異或(Bitwise XOR)運算符^,我們在第 1 節 “為什麼計算機用二進制計數”講過異或運算。下面用二進制的形式舉幾個例子。
注意,&、|、^運算符都是要做Usual Arithmetic Conversion的(其中有一步是Integer Promotion),~運算符也要做Integer Promotion,所以在C語言中其實並不存在8位整數的位運算,操作數在做位運算之前都至少被提升為int型了,上面用8位整數舉例只是為了書寫方便。比如:
unsigned char c = 0xfc; unsigned int i = ~c;
計算過程是這樣的:常量0xfc是int型的,賦給c要轉成unsigned char,值不變;c的十六進製表示是fc,計算~c時先提升為整型(000000fc)然後取反,最後結果是ffffff03。注意,如果把~c看成是8位整數的取反,最後結果就得3了,這就錯了。為了避免出錯,一是儘量避免不同類型之間的賦值,二是每一步計算都要按上一章講的類型轉換規則仔細檢查。
移位運算符(Bitwise Shift)包括左移<<和右移>>。左移將一個整數的各二進制位全部左移若干位,例如0xcfffffff3<<2得到0x3fffffcc:
最高兩位的11被移出去了,最低兩位又補了兩個0,其它位依次左移兩位。但要注意,移動的位數必須小於左操作數的總位數,比如上面的例子,左邊是unsigned int型,如果左移的位數大於等於32位,則結果是Undefined。移位運算符不同於+ - * / ==等運算符,兩邊操作數的類型不要求一致,但兩邊操作數都要做Integer Promotion,整個表達式的類型和左操作數提升後的類型相同。
複習一下第 2 節 “不同進制之間的換算”講過的知識可以得出結論,在一定的取值範圍內,將一個整數左移1位相當於乘以2。比如二進制11(十進制3)左移一位變成110,就是6,再左移一位變成1100,就是12。讀者可以自己驗證這條規律對有符號數和無符號數都成立,對負數也成立。當然,如果左移改變了最高位(符號位),那麼結果肯定不是乘以2了,所以我加了個前提“在一定的取值範圍內”。由於計算機做移位比做乘法快得多,編譯器可以利用這一點做優化,比如看到原始碼中有i * 8,可以編譯成移位指令而不是乘法指令。
當操作數是無符號數時,右移運算的規則和左移類似,例如0xcfffffff3>>2得到0x33fffffc:
最低兩位的11被移出去了,最高兩位又補了兩個0,其它位依次右移兩位。和左移類似,移動的位數也必須小於左操作數的總位數,否則結果是Undefined。在一定的取值範圍內,將一個整數右移1位相當於除以2,小數部分截掉。
當操作數是有符號數時,右移運算的規則比較複雜:
如果是正數,那麼高位移入0
如果是負數,那麼高位移入1還是0不一定,這是Implementation-defined的。對於x86平台的
gcc編譯器,最高位移入1,也就是仍保持負數的符號位,這種處理方式對負數仍然保持了“右移1位相當於除以2”的性質。
綜上所述,由於類型轉換和移位等問題,用有符號數做位運算是很不方便的,所以,建議只對無符號數做位運算,以減少出錯的可能。
1、下面兩行printf打印的結果有何不同?請讀者比較分析一下。%x轉換說明的含義詳見第 2.9 節 “格式化I/O函數”。
int i = 0xcffffff3;
printf("%x\n", 0xcffffff3>>2);
printf("%x\n", i>>2);如果要對一個整數中的某些位進行操作,怎樣表示這些位在整數中的位置呢?可以用掩碼(Mask)來表示。比如掩碼0x0000ff00表示對一個32位整數的8~15位進行操作,舉例如下。
1、取出8~15位。
unsigned int a, b, mask = 0x0000ff00; a = 0x12345678; b = (a & mask) >> 8; /* 0x00000056 */
這樣也可以達到同樣的效果:
b = (a >> 8) & ~(~0U << 8);
2、將8~15位清0。
unsigned int a, b, mask = 0x0000ff00; a = 0x12345678; b = a & ~mask; /* 0x12340078 */
3、將8~15位置1。
unsigned int a, b, mask = 0x0000ff00; a = 0x12345678; b = a | mask; /* 0x1234ff78 */
1、統計一個無符號整數的二進製表示中1的個數,函數原型是int countbit(unsigned int x);。
2、用位操作實現無符號整數的乘法運算,函數原型是unsigned int multiply(unsigned int x, unsigned int y);。例如:(11011)2×(10010)2=((11011)2<<1)+((11011)2<<4)。
3、對一個32位無符號整數做循環右移,函數原型是unsigned int rotate_right(unsigned int x);。所謂循環右移就是把低位移出去的部分再補到高位上去,例如rotate_right(0xdeadbeef, 16)的值應該是0xefdeadbe。
1、一個數和自己做異或的結果是0。如果需要一個常數0,x86平台的編譯器可能會生成這樣的指令:xorl %eax, %eax。不管eax寄存器裡的值原來是多少,做異或運算都能得到0,這條指令比同樣效果的movl $0, %eax指令快,因為前者只需要在CPU內部計算,而後者需要訪問內存,在下一章第 5 節 “Memory Hierarchy”詳細介紹。
2、從異或的真值表可以看出,不管是0還是1,和0做異或保持原值不變,和1做異或得到原值的相反值。可以利用這個特性配合掩碼實現某些位的翻轉,例如:
unsigned int a, b, mask = 1U << 6; a = 0x12345678; b = a ^ mask; /* flip the 6th bit */
3、如果a1 ^ a2 ^ a3 ^ ... ^ an的結果是1,則表示a1、a2、a3...an之中1的個數為奇數個,否則為偶數個。這條性質可用於奇偶校驗(Parity Check),比如在串口通信過程中,每個位元組的數據都計算一個校驗位,數據和校驗位一起發送出去,這樣接收方可以根據校驗位粗略地判斷接收到的數據是否有誤。
4、x ^ x ^ y == y,因為x ^ x == 0,0 ^ y == y。這個性質有什麼用呢?我們來看這樣一個問題:交換兩個變數的值,不得借助額外的存儲空間,所以就不能採用temp = a; a = b; b = temp;的辦法了。利用位運算可以這樣做交換:
a = a ^ b; b = b ^ a; a = a ^ b;
分析一下這個過程。為了避免混淆,把a和b的初值分別記為a0和b0。第一行,a = a0 ^ b0;第二行,把a的新值代入,得到b = b0 ^ a0 ^ b0,等號右邊的b0相當於上面公式中的x,a0相當於y,所以結果為a0;第三行,把a和b的新值代入,得到a = a0 ^ b0 ^ a0,結果為b0。注意這個過程不能把同一個變數自己跟自己交換,而利用中間變數temp則可以交換。