人類的計數方式通常是“逢十進一”，稱為十進制（Decimal），大概因為人有十個手指，所以十進制是最自然的計數方式，很多民族的語言文字中都有十個數字，而阿拉伯數字0~9是目前最廣泛採用的。

計算機是用數字電路搭成的，數字電路中只有1和0兩種狀態，或者可以說計算機只有兩個手指，所以對計算機來說二進制（Binary）是最自然的計數方式。根據“逢二進一”的原則，十進制的1、2、3、4分別對應二進制的1、10、11、100。二進制的一位數字稱為一個位（Bit），三個bit能夠表示的最大的二進制數是111，也就是十進制的7。不管用哪種計數方式，數的大小並沒有變，十進制的1+1等於2，二進制的1+1等於10，二進制的10和十進制的2大小是相等的。事實上，計算機採用如下的邏輯電路計算兩個bit的加法：

圖 14.1. 1-bit Full Adder

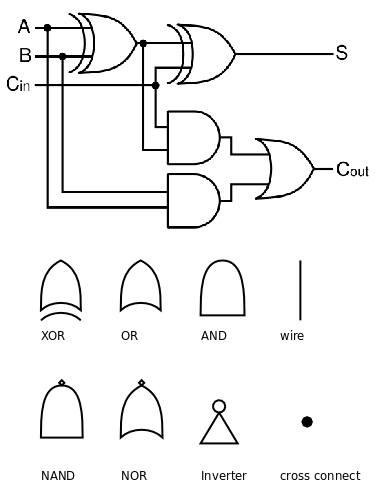
圖的上半部分（出自Wikipedia）的電路稱為一位全加器（1-bit Full Adder），圖的下半部分是一些邏輯電路符號的圖例。我們首先解釋這些圖例，邏輯電路由門電路（Gate）和導線（Wire）組成，同一條導線上在某一時刻的電壓值只能是高和低兩種狀態之一，分別用0和1表示。如果兩條導線短接在一起則它們的電壓值相同，在接點處畫一個黑點，如果接點處沒有畫黑點則表示這兩條綫並沒有短接在一起，只是在畫圖時無法避免交叉。導線的電壓值進入門電路的輸入端，經過邏輯運算後在門電路的輸出端輸出運算結果的電壓值，任何複雜的加減乘除運算都可以分解成簡單的邏輯運算。AND、OR和NOT運算在第 3 節 “布爾代數”中講過了，這三種邏輯運算分別用與門、或門和反相器（Inverter）實現。另外幾種邏輯運算在這裡補充一下。異或（XOR，eXclusive OR）運算的真值表如下：

用一句話概括就是：兩個操作數相同則結果為0，兩個操作數不同則結果為1。與非（NAND）和或非（NOR）運算就是在與、或運算的基礎上取反：

如果把與門、或門和反相器組合來實現NAND和NOR運算，則電路過于複雜了，因此邏輯電路中通常有專用的與非門和或非門。現在我們看看上圖中的AND、OR、XOR是怎麼實現兩個bit的加法的。A、B是兩個加數，C_in是低位傳上來的進位（Carry），相當於三個加數求和，三個加數都是0則結果為0，三個加數都是1則結果為11，即輸出位S是1，產生的進位C_out也是1。下面根據加法的規則用真值表列出所有可能的情況：

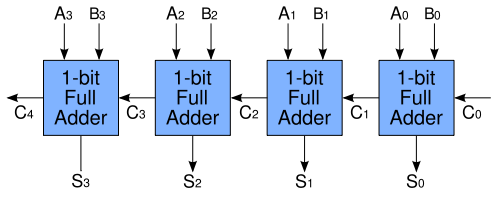
請讀者對照電路圖驗證一下真值表是否正確。如果把很多個一位全加器串接起來，就成了多位加法器，如下圖所示（該圖出自Wikipedia）：

圖 14.2. 4-bit Ripple Carry Adder

圖中的一位全加器用方框表示，上一級全加器的C_out連接到下一級全加器的C_in，讓進位像漣漪一樣一級一級傳開，所以叫做Ripple Carry Adder，這樣就可以把兩個4 bit二進制數A₃A₂A₁A₀和B₃B₂B₁B₀加起來了。在這裡介紹Ripple Carry Adder只是為了讓讀者理解計算機是如何通過邏輯運算來做算術運算的，實際上這種加法器效率很低，只能加完了一位再加下一位，更實用、更複雜的加法器可以多個位一起計算，有興趣的讀者可參考[數字邏輯基礎]。