3.3 遞歸數據結構
譯者:飛龍
在第二章中,我們引入了偶對的概念,作為一種將兩個對象結合為一個對象的機制。我們展示了偶對可以使用內建元素來實現。偶對的封閉性表明偶對的每個元素本身都可以為偶對。
這種封閉性允許我們實現遞歸列表的數據抽象,它是我們的第一種序列類型。遞歸列表可以使用遞歸函數最為自然地操作,就像它們的名稱和結構表示的那樣。在這一節中,我們會討論操作遞歸列表和其它遞歸結構的自定義的函數。
3.3.1 處理遞歸列表
遞歸列表結構將列表表示為首個元素和列表的剩餘部分的組合。我們之前使用函數實現了遞歸列表,但是現在我們可以使用類來重新實現。下面,長度(__len__)和元素選擇(__getitem__)被重寫來展示處理遞歸列表的典型模式。
>>> class Rlist(object):
"""A recursive list consisting of a first element and the rest."""
class EmptyList(object):
def __len__(self):
return 0
empty = EmptyList()
def __init__(self, first, rest=empty):
self.first = first
self.rest = rest
def __repr__(self):
args = repr(self.first)
if self.rest is not Rlist.empty:
args += ', {0}'.format(repr(self.rest))
return 'Rlist({0})'.format(args)
def __len__(self):
return 1 + len(self.rest)
def __getitem__(self, i):
if i == 0:
return self.first
return self.rest[i-1]
__len__和__getitem__的定義實際上是遞歸的,雖然不是那麼明顯。Python 內建函數len在自定義對象的參數上調用時會尋找叫做__len__的方法。與之類似,下標運算符會尋找叫做__getitem__的方法。於是,這些定義最後會調用對象自身。剩餘部分上的遞歸調用是遞歸列表處理的普遍模式。這個遞歸列表的類定義與 Python 的內建序列和打印操作能夠合理交互。
>>> s = Rlist(1, Rlist(2, Rlist(3)))
>>> s.rest
Rlist(2, Rlist(3))
>>> len(s)
3
>>> s[1]
2
創建新列表的操作能夠直接使用遞歸來表示。例如,我們可以定義extend_rlist函數,它接受兩個遞歸列表作為參數並將二者的元素組合到新列表中。
>>> def extend_rlist(s1, s2):
if s1 is Rlist.empty:
return s2
return Rlist(s1.first, extend_rlist(s1.rest, s2))
>>> extend_rlist(s.rest, s)
Rlist(2, Rlist(3, Rlist(1, Rlist(2, Rlist(3)))))
與之類似,在遞歸列表上映射函數展示了相似的模式:
>>> def map_rlist(s, fn):
if s is Rlist.empty:
return s
return Rlist(fn(s.first), map_rlist(s.rest, fn))
>>> map_rlist(s, square)
Rlist(1, Rlist(4, Rlist(9)))
過濾操作包括額外的條件語句,但是也擁有相似的遞歸結構。
>>> def filter_rlist(s, fn):
if s is Rlist.empty:
return s
rest = filter_rlist(s.rest, fn)
if fn(s.first):
return Rlist(s.first, rest)
return rest
>>> filter_rlist(s, lambda x: x % 2 == 1)
Rlist(1, Rlist(3))
列表操作的遞歸實現通常不需要局部賦值或者while語句。反之,遞歸列表可以作為函數調用的結果來拆分和構造。所以,它們擁有步驟數量和所需空間的線性增長度。
3.3.2 層次結構
層次結構產生於數據的封閉特性,例如,元組可以包含其它元組。考慮這個數值1到4的嵌套表示。
>>> ((1, 2), 3, 4)
((1, 2), 3, 4)
這個元組是個長度為 3 的序列,它的第一個元素也是一個元組。這個嵌套結構的盒子和指針的圖示表明,它可以看做擁有四個葉子的樹,每個葉子都是一個數值。
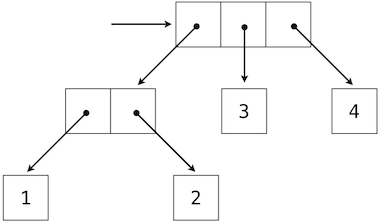
在樹中,每個子樹本身都是一棵樹。作為基本條件,任何本身不是元組的元素都是一個簡單的樹,沒有任何枝幹。也就是說,所有數值都是樹,就像在偶對(1, 2)和整個結構中那樣。
遞歸是用於處理樹形結構的自然工具,因為我們通常可以將樹的操作降至枝幹的操作,它會相應產生枝幹的枝幹的操作,以此類推,直到我們到達了樹的葉子。例如,我們可以實現count_leaves函數,它返回樹的葉子總數。
>>> t = ((1, 2), 3, 4)
>>> count_leaves(t)
4
>>> big_tree = ((t, t), 5)
>>> big_tree
((((1, 2), 3, 4), ((1, 2), 3, 4)), 5)
>>> count_leaves(big_tree)
9
正如map是用於處理序列的強大工具,映射和遞歸一起為樹的操作提供了強大而通用的計算形式。例如,我們可以使用高階遞歸函數map_tree 將樹的每個葉子平方,它的結構類似於count_leaves。
>>> def map_tree(tree, fn):
if type(tree) != tuple:
return fn(tree)
return tuple(map_tree(branch, fn) for branch in tree)
>>> map_tree(big_tree, square)
((((1, 4), 9, 16), ((1, 4), 9, 16)), 25)
**內部值。**上面描述的樹只在葉子上存在值。另一個通用的樹形結構表示也在樹的內部節點上存在值。我們使用類來表示這種樹。
>>> class Tree(object):
def __init__(self, entry, left=None, right=None):
self.entry = entry
self.left = left
self.right = right
def __repr__(self):
args = repr(self.entry)
if self.left or self.right:
args += ', {0}, {1}'.format(repr(self.left), repr(self.right))
return 'Tree({0})'.format(args)
例如,Tree類可以為fib的遞歸實現表示表達式樹中計算的值。fib函數用於計算斐波那契數。下面的函數fib_tree(n)返回Tree,它將第 n 個斐波那契樹作為entry,並將所有之前計算出來的斐波那契數存入它的枝幹中。
>>> def fib_tree(n):
"""Return a Tree that represents a recursive Fibonacci calculation."""
if n == 1:
return Tree(0)
if n == 2:
return Tree(1)
left = fib_tree(n-2)
right = fib_tree(n-1)
return Tree(left.entry + right.entry, left, right)
>>> fib_tree(5)
Tree(3, Tree(1, Tree(0), Tree(1)), Tree(2, Tree(1), Tree(1, Tree(0), Tree(1))))
這個例子表明,表達式樹可以使用樹形結構編程表示。嵌套表達式和樹形數據結構的聯繫,在我們這一章稍後對解釋器設計的討論中起到核心作用。
3.3.3 集合
除了列表、元組和字典之外,Python 擁有第四種容器類型,叫做set。集合字面值遵循元素以花括號閉合的數學表示。重複的元素在構造中會移除。集合是無序容器,所以打印出來的順序可能和元素在集合字面值中的順序不同。
>>> s = {3, 2, 1, 4, 4}
>>> s
{1, 2, 3, 4}
Python 的集合支持多種操作,包括成員測試、長度計算和標準的交集並集操作。
>>> 3 in s
True
>>> len(s)
4
>>> s.union({1, 5})
{1, 2, 3, 4, 5}
>>> s.intersection({6, 5, 4, 3})
{3, 4}
除了union和intersection,Python 的集合還支持多種其它操作。斷言isdisjoint、issubset和issuperset提供了集合比較操作。集合是可變的,並且可以使用add、remove、discard和pop一次修改一個元素。額外的方法提供了多元素的修改,例如clear和update。Python 集合文檔十分詳細並足夠易懂。
**實現集合。**抽象上,集合是不同對象的容器,支持成員測試、交集、並集和附加操作。向集合添加元素會返回新的集合,它包含原始集合的所有元素,如果沒有重複的話,也包含新的元素。並集和交集運算返回出現在任意一個或兩個集合中的元素構成的集合。就像任何數據抽象那樣,我們可以隨意實現任何集合表示上的任何函數,只要它們提供這種行為。
在這章的剩餘部分,我們會考慮三個實現集合的不同方式,它們在表示上不同。我們會通過分析集合操作的增長度,刻畫這些不同表示的效率。我們也會使用這一章之前的Rlist和Tree類,它們可以編寫用於集合元素操作的簡單而優雅的遞歸解決方案。
**作為無序序列的集合。**一種集合的表示方式是看做沒有出現多於一次的元素的序列。空集由空序列來表示。成員測試會遞歸遍歷整個列表。
>>> def empty(s):
return s is Rlist.empty
>>> def set_contains(s, v):
"""Return True if and only if set s contains v."""
if empty(s):
return False
elif s.first == v:
return True
return set_contains(s.rest, v)
>>> s = Rlist(1, Rlist(2, Rlist(3)))
>>> set_contains(s, 2)
True
>>> set_contains(s, 5)
False
這個set_contains 的實現需要Θ(n)的時間來測試元素的成員性,其中n是集合s的大小。使用這個線性時間的成員測試函數,我們可以將元素添加到集合中,也是線性時間。
>>> def adjoin_set(s, v):
"""Return a set containing all elements of s and element v."""
if set_contains(s, v):
return s
return Rlist(v, s)
>>> t = adjoin_set(s, 4)
>>> t
Rlist(4, Rlist(1, Rlist(2, Rlist(3))))
那麼問題來了,我們應該在設計表示時關注效率。計算兩個集合set1和set2的交集需要成員測試,但是這次每個set1的元素必須測試set2中的成員性,對於兩個大小為n的集合,這會產生步驟數量的平方增長度Θ(n^2)。
>>> def intersect_set(set1, set2):
"""Return a set containing all elements common to set1 and set2."""
return filter_rlist(set1, lambda v: set_contains(set2, v))
>>> intersect_set(t, map_rlist(s, square))
Rlist(4, Rlist(1))
在計算兩個集合的並集時,我們必須小心避免兩次包含任意一個元素。union_set 函數也需要線性數量的成員測試,同樣會產生包含Θ(n^2)步驟的過程。
>>> def union_set(set1, set2):
"""Return a set containing all elements either in set1 or set2."""
set1_not_set2 = filter_rlist(set1, lambda v: not set_contains(set2, v))
return extend_rlist(set1_not_set2, set2)
>>> union_set(t, s)
Rlist(4, Rlist(1, Rlist(2, Rlist(3))))
**作為有序元組的集合。**一種加速我們的集合操作的方式是修改表示,使集合元素遞增排列。為了這樣做,我們需要一些比較兩個對象的方式,使我們能判斷哪個更大。Python 中,許多不同對象類型都可以使用<和>運算符比較,但是我們會專注於這個例子中的數值。我們會通過將元素遞增排列來表示數值集合。
有序的一個優點會在set_contains體現:在檢查對象是否存在時,我們不再需要掃描整個集合。如果我們到達了大於要尋找的元素的集合元素,我們就知道這個元素不在集合中:
>>> def set_contains(s, v):
if empty(s) or s.first > v:
return False
elif s.first == v:
return True
return set_contains(s.rest, v)
>>> set_contains(s, 0)
False
這節省了多少步呢?最壞的情況中,我們所尋找的元素可能是集合中最大的元素,所以步驟數量和無序表示相同。另一方面,如果我們尋找許多不同大小的元素,我們可以預料到有時我們可以在列表開頭的位置停止搜索,其它情況下我們仍舊需要檢測整個列表。平均上我們應該需要檢測集合中一半的元素。所以,步驟數量的平均值應該是n/2。這還是Θ(n)的增長度,但是它確實會在平均上為我們節省之前實現的一半步驟數量。
我們可以通過重新實現intersect_set獲取更加可觀的速度提升。在無序表示中,這個操作需要Θ(n^2)的步驟,因為我們對set1的每個元素執行set2上的完整掃描。但是使用有序的實現,我們可以使用更加機智的方式。我們同時迭代兩個集合,跟蹤set1中的元素e1和set2中的元素e2。當e1和e2相等時,我們在交集中添加該元素。
但是,假設e1小於e2,由於e2比set2的剩餘元素更小,我們可以立即推斷出e1不會出現在set2剩餘部分的任何位置,因此也不會出現在交集中。所以,我們不再需要考慮e1,我們將它丟棄並來到set1的下一個元素。當e2 < e1時,我們可以使用相似的邏輯來步進set2中的元素。下面是這個函數:
>>> def intersect_set(set1, set2):
if empty(set1) or empty(set2):
return Rlist.empty
e1, e2 = set1.first, set2.first
if e1 == e2:
return Rlist(e1, intersect_set(set1.rest, set2.rest))
elif e1 < e2:
return intersect_set(set1.rest, set2)
elif e2 < e1:
return intersect_set(set1, set2.rest)
>>> intersect_set(s, s.rest)
Rlist(2, Rlist(3))
為了估計這個過程所需的步驟數量,觀察每一步我們都縮小了至少集合的一個元素的大小。所以,所需的步驟數量最多為set1和set2的大小之和,而不是無序表示所需的大小之積。這是Θ(n)而不是Θ(n^2)的增長度 -- 即使集合大小適中,它也是一個相當可觀的加速。例如,兩個大小為100的集合的交集需要 200步,而不是無序表示的 10000 步。
表示為有序序列的集合的添加和並集操作也以線性時間計算。這些實現都留做練習。
**作為二叉樹的集合。**我們可以比有序列表表示做得更好,通過將幾個元素重新以樹的形式排列。我們使用之前引入的Tree類。樹根的entry持有集合的一個元素。left分支的元素包括所有小於樹根元素的元素。right分支的元素包括所有大於樹根元素的元素。下面的圖展示了一些樹,它們表示集合{1, 3, 5, 7, 9, 11}。相同的集合可能會以不同形式的樹來表示。有效表示所需的唯一條件就是所有left子樹的元素應該小於entry,並且所有right子樹的元素應該大於它。
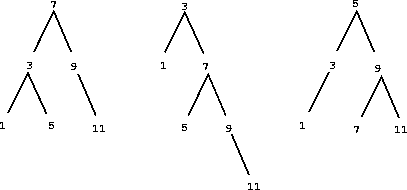
樹形表示的優點是:假設我們打算檢查v是否在集合中。我們通過將v於entry比較開始。如果v小於它,我們就知道了我們只需要搜索left子樹。如果v大於它,我們只需要搜索right子樹。現在如果樹是“平衡”的,每個這些子樹都約為整個的一半大小。所以,每一步中我們都可以將大小為n的樹的搜索問題降至搜索大小為n/2的子樹。由於樹的大小在每一步減半,我們應該預料到,用戶搜索樹的步驟以Θ(log n)增長。比起之前的表示,它的速度對於大型集合有可觀的提升。set_contains 函數利用了樹形集合的有序結構:
>>> def set_contains(s, v):
if s is None:
return False
elif s.entry == v:
return True
elif s.entry < v:
return set_contains(s.right, v)
elif s.entry > v:
return set_contains(s.left, v)
向集合添加元素與之類似,並且也需要Θ(log n)的增長度。為了添加值v,我們將v與entry比較,來決定v應該添加到right還是left分支,以及是否已經將v添加到了合適的分支上。我們將這個新構造的分支與原始的entry和其它分支組合。如果v等於entry,我們就可以返回這個節點。如果我們被要求將v添加到空的樹中,我們會生成一個Tree,它包含v作為entry,並且left和right都是空的分支。下面是這個函數:
>>> def adjoin_set(s, v):
if s is None:
return Tree(v)
if s.entry == v:
return s
if s.entry < v:
return Tree(s.entry, s.left, adjoin_set(s.right, v))
if s.entry > v:
return Tree(s.entry, adjoin_set(s.left, v), s.right)
>>> adjoin_set(adjoin_set(adjoin_set(None, 2), 3), 1)
Tree(2, Tree(1), Tree(3))
搜索該樹可以以對數步驟數量執行,我們這個敘述基於樹是“平衡”的假設。也就是說,樹的左子樹和右子樹都擁有相同數量的相應元素,使每個子樹含有母樹一半的元素。但是我們如何確定,我們構造的樹就是平衡的呢?即使我們以一顆平衡樹開始,使用adjoin_set添加元素也會產生不平衡的結果。由於新添加的元素位置取決於如何將元素與集合中的已有元素比較,我們可以預測,如果我們“隨機”添加元素到樹中,樹在平均上就會趨向於平衡。
但是這不是一個保證。例如,如果我們以空集開始,並向序列中添加 1 到 7,我們就會在最後得到很不平衡的樹,其中所有左子樹都是空的,所以它與簡單的有序列表相比並沒有什麼優勢。一種解決這個問題的方式是定義一種操作,它將任意的樹轉換為具有相同元素的平衡樹。我們可以在每個adjoin_set操作之後執行這個轉換來保證我們的集合是平衡的。
交集和並集操作可以在樹形集合上以線性時間執行,通過將它們轉換為有序的列表,並轉換回來。細節留做練習。
**Python 集合實現。**Python 內建的set類型並沒有使用上述任意一種表示。反之,Python 使用了一種實現,它的成員測試和添加操作是(近似)常量時間的,基於一種叫做哈希(散列)的機制,這是其它課程的話題。內建的 Python 集合不能包含可變的數據類型,例如列表、字典或者其它集合。為了能夠嵌套集合,Python 也提供了一種內建的不可變frozenset 類,除了可變操作和運算符之外,它擁有和set相同的方法。