SICP Python 描述 中文版

原文：CS61A: Online Textbook

譯者：飛龍

• 在線閱讀
• PDF格式
• EPUB格式
• MOBI格式
• Github

贊助我

協議

CC BY-NC-SA 4.0

第一章 使用函數構建抽象

1.1 引言

來源：1.1 Introduction

譯者：飛龍

協議：CC BY-NC-SA 4.0

計算機科學是一個極其寬泛的學科。全球的分佈式系統、人工智能、機器人、圖形、安全、科學計算，計算機體系結構和許多新興的二級領域，每年都會由於新技術和新發現而擴展。計算機科學的快速發展廣泛影響了人類生活。商業、通信、科學、藝術、休閒和政治都被計算機領域徹底改造。

計算機科學的巨大生產力可能只是因為它構建在一系列優雅且強大的基礎概念上。所有計算都以表達信息、指定處理它所需的邏輯、以及設計管理邏輯複雜性的抽象作為開始。對這些基礎的掌握需要我們精確理解計算機如何解釋程序以及執行計算過程。

這些基礎概念在伯克利長期教授，使用由Harold Abelson、Gerald Jay Sussman和Julie Sussman創作的經典教科書《計算機科學的構造與解釋》（SICP）。這個講義大量借鑑了這本書，原作者慷慨地使它可用於改編和複用。

我們的智力之旅一旦出發就不能回頭了，我們也永遠都不應該對此有所期待。

我們將要學習計算過程的概念。計算過程是計算機中的抽象事物。在演化中，過程操縱著叫做數據的其它事物。過程的演化由叫做程序的一系列規則主導。人們創造程序來主導過程。實際上，我們使用我們的咒語來憑空創造出計算機的靈魂。

我們用於創造過程的程序就像巫師的魔法。它們由一些古怪且深奧的編程語言中的符號表達式所組成，這些語言指定了我們想讓過程執行的任務。

在一臺工作正確的計算機上，計算過程準確且嚴謹地執行程序。所以，就像巫師的學徒那樣，程序員新手必須學會理解和預測他們的魔法產生的結果。

--Abelson & Sussman, SICP (1993)

1.1.1 在Python中編程

語言並不是你學到的東西，而是你參與的東西。

--Arika Okrent

為了定義計算過程，我們需要一種編程語言，最好是一種許多人和大量計算機都能懂的語言。這門課中，我們將會使用Python語言。

Python是一種廣泛使用的編程語言，並且在許多職業中都有它的愛好者：Web程序員、遊戲工程師、科學家、學者，甚至新編程語言的設計師。當你學習Python時，你就加入到了一個數百萬人的開發者社群。開發者社群是一個極其重要的組織：成員可以互相幫助來解決問題，分享他們的代碼和經驗，以及一起開發軟件和工具。投入的成員經常由於他們的貢獻而出名，並且收到廣泛的尊重。也許有一天你會被提名為Python開發者精英。

Python語言自身就是一個大型志願者社群的產物，並且為其貢獻者的多元化而自豪。這種語言在20世紀80年代末由Guido van Rossum設計並首次實現。他的Python3教程的第一章解釋了為什麼Python在當今眾多語言之中如此流行。

Python適用於作為教學語言，因為縱觀它的歷史，Python的開發者強調了Python代碼對人類的解釋性，並在Python之禪中美觀、簡約和可讀的原則下進一步加強。Python尤其適用於課堂，因為它寬泛的特性支持大量的不同編程風格，我們將要探索它們。在Python中編程沒有單一的解法，但是有一些習俗在開發者社群之間流傳，它們可以使現有程序的閱讀、理解，以及擴展變得容易。所以，Python的靈活性和易學性的組合可以讓學生們探索許多編程範式，之後將它們新學到的知識用於數千個正在開發的項目中。

這些講義通過使用抽象設計的技巧和嚴謹的計算模型，來快速介紹Python的特性。此外，這些講義提供了Python編程的實踐簡介，包含一些高級語言特性和展示示例。通過這門課，學習Python將會變成自然而然的事情。

然而，Python是一門生態豐富的語言，帶有大量特性和用法。我們講到基本的計算機科學概念時，會刻意慢慢地介紹他們。對於有經驗的學生，他們打算一口氣學完語言的所有細節，我們推薦他們閱讀Mark Pilgrim的書Dive Into Python 3，它在網上可以免費閱讀。這本書的主題跟這門課極其不同，但是這本書包含了許多關於使用Python的寶貴的實用信息。事先告知：不像這些講義，Dive Into Python 3需要一些編程經驗。

開始在Python中編程的最佳方法就是直接和解釋器交互。這一章會描述如何安裝Python3，使用解釋器開始交互式會話，以及開始編程。

1.1.2 安裝Python3

就像所有偉大的軟件一樣，Python具有許多版本。這門課會使用Python3最新的穩定版本（本書編寫時是3.2）。許多計算機都已經安裝了Python的舊版本，但是它們可能不滿足這門課。你應該可以在這門課上使用任何能安裝Python3的計算機。不要擔心，Python是免費的。

Dive Into Python 3擁有一個為所有主流平臺準備的詳細的安裝指南。這個指南多次提到了Python3.1，但是你最好安裝3.2（雖然它們的差異在這門課中非常微小）。EECS學院的所有教學機都已經安裝了Python3.2。

1.1.3 交互式會話

在Python交互式會話中，你可以在提示符>>>之後鍵入一些Python代碼。Python解釋器讀取並求出你輸入的東西，並執行你的各種命令。

有幾種開始交互式會話的途徑，並且具有不同的特性。把它們嘗試一遍來找出你最喜歡的方式。它們全部都在背後使用了相同的解釋器（CPython）。

• 最簡單且最普遍的方式就是運行Python3應用。在終端提示符後（Mac/Unix/Linux）鍵入python3，或者在Windows上打開Python3應用。（譯者注：Windows上設置完Python的環境變量之後，就可以在cmd或PowerShell中執行相同操作了。）
• 有一個更加用戶友好的應用叫做Idle3（idle3），可用於學習這門語言。Idle會高亮你的代碼（叫做語法高亮），彈出使用提示，並且標記一些錯誤的來源。Idle總是由Python自帶，所以你已經安裝它了。
• Emacs編輯器可以在它的某個緩衝區中運行交互式會話。雖然它學習起來有些挑戰，Emacs是個強大且多功能的編輯器，適用於任何語言。請閱讀61A的Emacs教程來開始。許多程序員投入大量時間來學習Emacs，之後他們就不再切換編輯器了。

在所有情況中，如果你看見了Python提示符>>>，你就成功開啟了交互式會話。這些講義使用提示符來展示示例，同時帶有一些輸入。

>>> 2 + 2
4

控制：每個會話都保留了你的歷史輸入。為了訪問這些歷史，需要按下<Control>-P（上一個）和<Control>-N（下一個）。<Control>-D會退出會話，這會清除所有歷史。

1.1.4 第一個例子

想像會把不知名的事物用一種形式呈現出來，詩人的筆再使它們具有如實的形象，空虛的無物也會有了居處和名字。

--威廉·莎士比亞，《仲夏夜之夢》

為了介紹Python，我們會從一個使用多個語言特性的例子開始。下一節中，我們會從零開始，一步一步構建整個語言。你可以將這章視為即將到來的特性的預覽。

Python擁有常見編程功能的內建支持，例如文本操作、顯示圖形以及互聯網通信。導入語句

>>> from urllib.request import urlopen

為訪問互聯網上的數據加載功能。特別是，它提供了叫做urlopen的函數，可以訪問到統一資源定位器（URL）處的內容，它是互聯網上的某個位置。

**語句和表達式：**Python代碼包含語句和表達式。廣泛地說，計算機程序包含的語句

1. 計算某個值
2. 或執行某個操作

語句通常用於描述操作。當Python解釋器執行語句時，它執行相應操作。另一方面，表達式通常描述產生值的運算。當Python求解表達式時，就會計算出它的值。這一章介紹了幾種表達式和語句。

賦值語句

>>> shakespeare = urlopen('http://inst.eecs.berkeley.edu/~cs61a/fa11/shakespeare.txt')

將名稱shakespeare和後面的表達式的值關聯起來。這個表達式在URL上調用urlopen函數，URL包含了莎士比亞的37個劇本的完整文本，在單個文本文件中。

**函數：**函數封裝了操作數據的邏輯。Web地址是一塊數據，莎士比亞的劇本文本是另一塊數據。前者產生後者的過程可能有些複雜，但是我們可以只通過一個表達式來調用它們，因為複雜性都塞進函數里了。函數是這一章的主要話題。

另一個賦值語句

>>> words = set(shakespeare.read().decode().split())

將名稱words關聯到出現在莎士比亞劇本中的所有去重詞彙的集合，總計33,721個。這個命令鏈調用了read、decode和split，每個都操作銜接的計算實體：從URL讀取的數據、解碼為文本的數據、以及分割為單詞的文本。所有這些單詞都放在set中。

**對象：**集合是一種對象，它支持取交和測試成員的操作。對象整合了數據和操作數據的邏輯，並以一種隱藏其複雜性的方式。對象是第二章的主要話題。

表達式

>>> {w for w in words if len(w) >= 5 and w[::-1] in words}
{'madam', 'stink', 'leets', 'rever', 'drawer', 'stops', 'sessa',
'repaid', 'speed', 'redder', 'devil', 'minim', 'spots', 'asses',
'refer', 'lived', 'keels', 'diaper', 'sleek', 'steel', 'leper',
'level', 'deeps', 'repel', 'reward', 'knits'}

是一個複合表達式，求出正序或倒序出現的“莎士比亞詞彙”集合。神秘的記號w[::-1]遍歷單詞中的每個字符，然而-1表明倒序遍歷（::表示第一個和最後一個單詞都使用默認值）。當你在交互式會話中輸入表達式時，Python會在隨後打印出它的值，就像上面那樣。

**解釋器：**複合表達式的求解需要可預測的過程來精確執行解釋器的代碼。執行這個過程，並求解複合表達式和語句的程序就叫解釋器。解釋器的設計與實現是第三章的主要話題。

與其它計算機程序相比，編程語言的解釋器通常比較獨特。Python在意圖上並沒有按照莎士比亞或者回文來設計，但是它極大的靈活性讓我們用極少的代碼處理大量文本。

最後，我們會發現，所有這些核心概念都是緊密相關的：函數是對象，對象是函數，解釋器是二者的實例。然而，對這些概念，以及它們在代碼組織中的作用的清晰理解，是掌握編程藝術的關鍵。

1.1.5 實踐指南

Python正在等待你的命令。你應當探索這門語言，即使你可能不知道完整的詞彙和結構。但是，要為錯誤做好準備。雖然計算機極其迅速和靈活，它們也十分古板。在斯坦福的導論課中，計算機的本性描述為

計算機的基本等式是：計算機 = 強大 + 笨拙

計算機非常強大，能夠迅速搜索大量數據。計算機每秒可以執行數十億次操作，其中每個操作都非常簡單。

計算機也非常笨拙和脆弱。它們所做的操作十分古板、簡單和機械化。計算機缺少任何類似真實洞察力的事情...它並不像電影中的HAL 9000。如果不出意外，你不應被計算機嚇到，就像它擁有某種大腦一樣。它在背後非常機械化。

程序是一個人使用他的真實洞察力來構建出的一些實用的東西，它由這些簡單的小操作所組成。

—Francisco Cai & Nick Parlante, 斯坦福 CS101

在你實驗Python解釋器的時候，你會馬上意識到計算機的古板：即使最小的拼寫和格式修改都會導致非預期的輸出和錯誤。

學習解釋錯誤和診斷非預期錯誤的原因叫做調試（debugging）。它的一些指導原則是：

1. 逐步測試：每個寫好的程序都由小型的組件模塊組成，這些組件可以獨立測試。儘快測試你寫好的任何東西來及早捕獲錯誤，並且從你的組件中獲得自信。
2. 隔離錯誤：複雜程序的輸出、表達式、或語句中的錯誤，通常可以歸於特定的組件模塊。當嘗試診斷問題時，在你能夠嘗試修正錯誤之前，一定要將它跟蹤到最小的代碼片段。
3. 檢查假設：解釋器將你的指令執行為文字 -- 不多也不少。當一些代碼不匹配程序員所相信的（或所假設的）行為，它們的輸出就會是非預期的。瞭解你的假設，之後專注於驗證你的假設是否整理來調試。
4. 詢問他人：你並不是一個人！如果你不理解某個錯誤信息，可以詢問朋友、導師或者搜索引擎。如果你隔離了一個錯誤，但是不知道如何改正，可以讓其它人來看一看。在小組問題解決中，會分享一大堆有價值的編程知識。

逐步測試、模塊化設計、明確假設和團隊作業是貫穿這門課的主題。但願它們也能夠一直伴隨你的計算機科學生涯。

1.2 編程元素

來源：1.2 The Elements of Programming

譯者：飛龍

協議：CC BY-NC-SA 4.0

編程語言是操作計算機來執行任務的手段，它也在我們組織關於過程的想法中，作為一種框架。程序用於在編程社群的成員之間交流這些想法。所以，程序必須為人類閱讀而編寫，並且僅僅碰巧可以讓機器執行。

當我們描述一種語言時，我們應該特別注意這種語言的手段，來將簡單的想法組合為更復雜的想法。每個強大的語言都擁有用於完成下列任務的機制：

• 基本的表達式和語句，它們由語言提供，表示最簡單的構建代碼塊。
• 組合的手段，複雜的元素由簡單的元素通過它來構建，以及
• 抽象的手段，複雜的元素可以通過它來命名，以及作為整體來操作。

在編程中，我們處理兩種元素：函數和數據。（不久之後我們就會探索它們並不是真的非常不同。）不正式地說，數據是我們想要操作的東西，函數描述了操作數據的規則。所以，任何強大的編程語言都應該能描述基本數據和基本函數，並且應該擁有組合和抽象二者的方式。

1.2.1 表達式

在實驗 Python 解釋器之後，我們現在必須重新開始，按照順序一步步地探索 Python 語言。如果示例看上去很簡單，要有耐心 -- 更刺激的東西還在後面。

我們以基本表達式作為開始。一種基本表達式就是數值。更精確地說，是你鍵入的，由 10 進制數字表示的數值組成的表達式。

>>> 42
42

表達式表示的數值也許會和算數運算符組合，來形成複合表達式，解釋器會求出它：

>>> -1 - -1
0
>>> 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
0.9921875

這些算術表達式使用了中綴符號，其中運算符（例如+、-、*、/）出現在操作數（數值）中間。Python包含許多方法來形成複合表達式。我們不會嘗試立即將它們列舉出來，而是在進行中介紹新的表達式形式，以及它們支持的語言特性。

1.2.2 調用表達式

最重要的複合表達式就是調用表達式，它在一些參數上調用函數。回憶代數中，函數的數學概念是一些輸入值到輸出值的映射。例如，max函數將它的輸入映射到單個輸出，輸出是輸入中的最大值。Python 中的函數不僅僅是輸入輸出的映射，它表述了計算過程。但是，Python 表示函數的方式和數學中相同。

>>> max(7.5, 9.5)
9.5

調用表達式擁有子表達式：運算符在圓括號之前，圓括號包含逗號分隔的操作數。運算符必須是個函數，操作數可以是任何值。這裡它們都是數值。當求解這個調用表達式時，我們說max函數以參數 7.5 和 9.5 調用，並且返回 9.5。

調用表達式中的參數的順序極其重要。例如，函數pow計算第一個參數的第二個參數次方。

>>> pow(100, 2)
10000
>>> pow(2, 100)
1267650600228229401496703205376

函數符號比中綴符號的數學慣例有很多優點。首先，函數可以接受任何數量的參數：

>>> max(1, -2, 3, -4)
3

不會產生任何歧義，因為函數的名稱永遠在參數前面。

其次，函數符號可以以直接的方式擴展為嵌套表達式，其中元素本身是複合表達式。在嵌套的調用表達式中，不像嵌套的中綴表達式，嵌套結構在圓括號中非常明顯。

>>> max(min(1, -2), min(pow(3, 5), -4))
-2

（理論上）這種嵌套沒有任何限制，並且 Python 解釋器可以解釋任何複雜的表達式。然而，人們可能會被多級嵌套搞暈。你作為程序員的一個重要作用就是構造你自己、你的同伴以及其它在未來可能會閱讀你代碼的人可以解釋的表達式。

最後，數學符號在形式上多種多樣：星號表示乘法，上標表示乘方，橫槓表示除法，屋頂和側壁表示開方。這些符號中一些非常難以打出來。但是，所有這些複雜事物可以通過調用表達式的符號來統一。雖然 Python 通過中綴符號（比如+和-）支持常見的數學運算符，任何運算符都可以表示為帶有名字的函數。

1.2.3 導入庫函數

Python 定義了大量的函數，包括上一節提到的運算符函數，但是通常不能使用它們的名字，這樣做是為了避免混亂。反之，它將已知的函數和其它東西組織在模塊中，這些模塊組成了 Python 庫。需要導入它們來使用這些元素。例如，math模塊提供了大量的常用數學函數：

>>> from math import sqrt, exp
>>> sqrt(256)
16.0
>>> exp(1)
2.718281828459045

operator模塊提供了中綴運算符對應的函數：

>>> from operator import add, sub, mul
>>> add(14, 28)
42
>>> sub(100, mul(7, add(8, 4)))
16

import語句標明瞭模塊名稱（例如operator或math），之後列出被導入模塊的具名屬性（例如sqrt和exp）。

Python 3 庫文檔列出了定義在每個模塊中的函數，例如數學模塊。然而，這個文檔為了解整個語言的開發者編寫。到現在為止，你可能發現使用函數做實驗會比閱讀文檔告訴你更多它的行為。當你更熟悉 Python 語言和詞彙時，這個文檔就變成了一份有價值的參考來源。

1.2.4 名稱和環境

編程語言的要素之一是它提供的手段，用於使用名稱來引用計算對象。如果一個值被給予了名稱，我們就說這個名稱綁定到了值上面。

在 Python 中，我們可以使用賦值語句來建立新的綁定，它包含=左邊的名稱和右邊的值。

>>> radius = 10
>>> radius
10
>>> 2 * radius
20

名稱也可以通過import語句綁定：

>>> from math import pi
>>> pi * 71 / 223
1.0002380197528042

我們也可以在一個語句中將多個值賦給多個名稱，其中名稱和表達式由逗號分隔：

>>> area, circumference = pi * radius * radius, 2 * pi * radius
>>> area
314.1592653589793
>>> circumference
62.83185307179586

=符號在 Python（以及許多其它語言）中叫做賦值運算符。賦值是 Python 中的最簡單的抽象手段，因為它使我們可以使用最簡單的名稱來引用複合操作的結果，例如上面計算的area。這樣，複雜的程序可以由複雜性遞增的計算對象一步一步構建，

將名稱綁定到值上，以及隨後通過名稱來檢索這些值的可能，意味著解釋器必須維護某種內存來跟蹤這些名稱和值的綁定。這些內存叫做環境。

名稱也可以綁定到函數。例如，名稱max綁定到了我們曾經用過的max函數上。函數不像數值，不易於渲染成文本，所以 Python 使用識別描述來代替，當我們打印函數時：

>>> max
<built-in function max>

我們可以使用賦值運算符來給現有函數起新的名字：

>>> f = max
>>> f
<built-in function max>
>>> f(3, 4)
4

成功的賦值語句可以將名稱綁定到新的值：

>>> f = 2
>>> f
2

在 Python 中，通過賦值綁定的名稱通常叫做變量名稱，因為它們在執行程序期間可以綁定到許多不同的值上面。

1.2.5 嵌套表達式的求解

我們這章的目標之一是隔離程序化思考相關的問題。作為一個例子，考慮嵌套表達式的求解，解釋器自己會遵循一個過程：

為了求出調用表達式，Python 會執行下列事情：

• 求出運算符和操作數子表達式，之後
• 在值為操作數子表達式的參數上調用值為運算符子表達式的函數。

這個簡單的過程大體上展示了一些過程上的重點。第一步表明為了完成調用表達式的求值過程，我們首先必須求出其它表達式。所以，求值過程本質上是遞歸的，也就是說，它會調用其自身作為步驟之一。

例如，求出

>>> mul(add(2, mul(4, 6)), add(3, 5))
208

需要應用四次求值過程。如果我們將每個需要求解的表達式抽出來，我們可以可視化這一過程的層次結構：

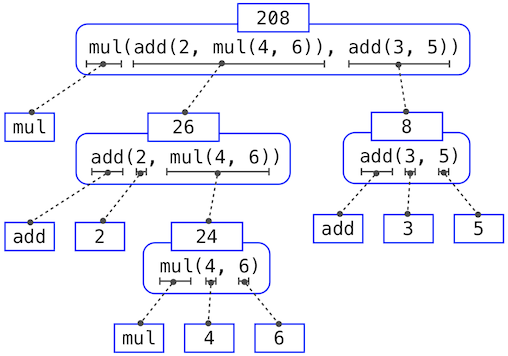
這個示例叫做表達式樹。在計算機科學中，樹從頂端向下生長。每一點上的對象叫做節點。這裡它們是表達式和它們的值。

求出根節點，也就是整個表達式，需要首先求出枝幹節點，也就是子表達式。葉子節點（也就是沒有子節點的節點）的表達式表示函數或數值。內部節點分為兩部分：表示我們想要應用的求值規則的調用表達式，以及表達式的結果。觀察這棵樹中的求值，我們可以想象操作數的值向上流動，從葉子節點開始，在更高的層上融合。

接下來，觀察第一步的重複應用，這會將我們帶到需要求值的地方，並不是調用表達式，而是基本表達式，例如數字（比如2），以及名稱（比如add），我們需要規定下列事物來謹慎對待基本的東西：

• 數字求值為它標明的數值，
• 名稱求值為當前環境中這個名稱所關聯的值

要注意環境的關鍵作用是決定表達式中符號的含義。Python 中，在不指定任何環境信息，來提供名稱x（以及名稱add）的含義的情況下，談到這樣一個表達式的值沒有意義：

>>> add(x, 1)

環境提供了求值所發生的上下文，它在我們理解程序執行中起到重要作用。

這個求值過程並不符合所有 Python 代碼的求解，僅僅是調用表達式、數字和名稱。例如，它並不能處理賦值語句。

>>> x = 3

的執行並不返回任何值，也不求解任何參數上的函數，因為賦值的目的是將一個名稱綁定到一個值上。通常，語句不會被求值，而是被執行，它們不產生值，但是會改變一些東西。每種語句或表達式都有自己的求值或執行過程，我們會在涉及時逐步介紹。

注：當我們說“數字求值為數值”的時候，我們的實際意思是 Python 解釋器將數字求解為數值。Python 的解釋器使編程語言具有了這個意義。假設解釋器是一個固定的程序，行為總是一致，我們就可以說數字（以及表達式）自己在 Python 程序的上下文中會求解為值。

1.2.6 函數圖解

當我們繼續構建求值的形式模型時，我們會發現解釋器內部狀態的圖解有助於我們跟蹤求值過程的發展。這些圖解的必要部分是函數的表示。

**純函數：**具有一些輸入（參數）以及返回一些輸出（調用結果）的函數。內建函數

>>> abs(-2)
2

可以描述為接受輸入併產生輸出的小型機器。

abs是純函數。純函數具有一個特性，調用它們時除了返回一個值之外沒有其它效果。

**非純函數：**除了返回一個值之外，調用非純函數會產生副作用，這會改變解釋器或計算機的一些狀態。一個普遍的副作用就是在返回值之外生成額外的輸出，例如使用print函數：

>>> print(-2)
-2
>>> print(1, 2, 3)
1 2 3

雖然這些例子中的print和abs看起來很像，但它們本質上以不同方式工作。print的返回值永遠是None，它是一個 Python 特殊值，表示沒有任何東西。Python 交互式解釋器並不會自動打印None值。這裡，print自己打印了輸出，作為調用中的副作用。

調用print的嵌套表達式會凸顯出它的非純特性：

>>> print(print(1), print(2))
1
2
None None

如果你發現自己不能預料到這個輸出，畫出表達式樹來弄清為什麼這個表達式的求值會產生奇怪的輸出。

要當心print！它的返回值為None，意味著它不應該在賦值語句中用作表達式：

>>> two = print(2)
2
>>> print(two)
None

**簽名：**不同函數具有不同的允許接受的參數數量。為了跟蹤這些必備條件，我們需要以一種展示函數名稱和參數名稱的方式，畫出每個函數。abs函數值接受一個叫作number的參數，向它提供更多或更少的參數會產生錯誤。print函數可以接受任意數量的參數，所以它渲染為print(...)。函數的可接受參數的描述叫做函數的簽名。

1.3 定義新的函數

來源：1.3 Defining New Functions

譯者：飛龍

協議：CC BY-NC-SA 4.0

我們已經在 Python 中認識了一些在任何強大的編程語言中都會出現的元素：

1. 數值是內建數據，算數運算是函數。
2. 嵌套函數提供了組合操作的手段。
3. 名稱到值的綁定提供了有限的抽象手段。

現在我們將要了解函數定義，一個更加強大的抽象技巧，名稱通過它可以綁定到複合操作上，並可以作為一個單元來引用。

我們通過如何表達“平方”這個概念來開始。我們可能會說，“對一個數求平方就是將這個數乘上它自己”。在 Python 中就是：

>>> def square(x):
        return mul(x, x)

這定義了一個新的函數，並賦予了名稱square。這個用戶定義的函數並不內建於解釋器。它表示將一個數乘上自己的複合操作。定義中的x叫做形式參數，它為被乘的東西提供一個名稱。這個定義創建了用戶定義的函數，並且將它關聯到名稱square上。

函數定義包含def語句，它標明瞭<name>（名稱）和一列帶有名字的<formal parameters>（形式參數）。之後，return（返回）語句叫做函數體，指定了函數的<return expression>（返回表達式），它是函數無論什麼時候調用都需要求值的表達式。

def <name>(<formal parameters>):
    return <return expression>

第二行必須縮進！按照慣例我們應該縮進四個空格，而不是一個Tab，返回表達式並不是立即求值，它儲存為新定義函數的一部分，並且只在函數最終調用時會被求出。（很快我們就會看到縮進區域可以跨越多行。）

定義了square之後，我們使用調用表達式來調用它：

>>> square(21)
441
>>> square(add(2, 5))
49
>>> square(square(3))
81

我們也可以在構建其它函數時，將square用作構建塊。列入，我們可以輕易定義sum_squares函數，它接受兩個數值作為參數，並返回它們的平方和：

>>> def sum_squares(x, y):
        return add(square(x), square(y))
>>> sum_squares(3, 4)
25

用戶定義的函數和內建函數以同種方法使用。確實，我們不可能在sum_squares的定義中分辨出square是否構建於解釋器中，從模塊導入還是由用戶定義。

1.3.1 環境

我們的 Python 子集已經足夠複雜了，但程序的含義還不是非常明顯。如果形式參數和內建函數具有相同名稱會如何呢？兩個函數是否能共享名稱而不會產生混亂呢？為了解決這些疑問，我們必須詳細描述環境。

表達式求值所在的環境由幀的序列組成，它們可以表述為一些盒子。每一幀都包含了一些綁定，它們將名稱和對應的值關聯起來。全局幀只有一個，它包含所有內建函數的名稱綁定（只展示了abs和max）。我們使用地球符號來表示全局。

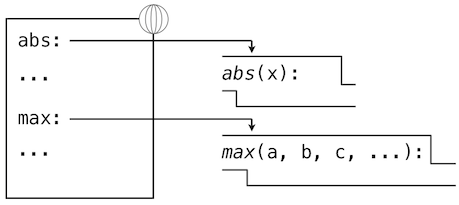
賦值和導入語句會向當前環境的第一個幀添加條目。到目前為止，我們的環境只包含全局幀。

>>> from math import pi
>>> tau = 2 * pi

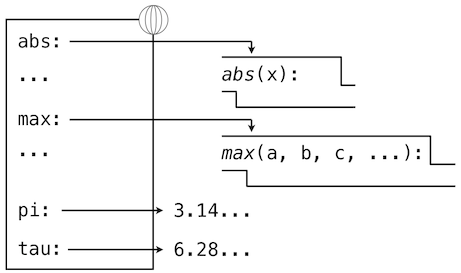
def語句也將綁定綁定到由定義創建的函數上。定義square之後的環境如圖所示：

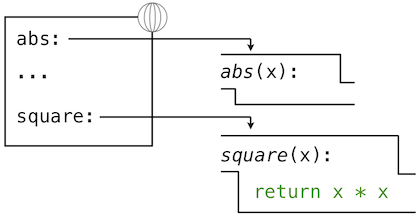
這些環境圖示展示了當前環境中的綁定，以及它們所綁定的值（並不是任何幀的一部分）。要注意函數名稱是重複的，一個在幀中，另一個是函數的一部分。這一重複是有意的，許多不同的名字可能會引用相同函數，但是函數本身只有一個內在名稱。但是，在環境中由名稱檢索值只檢查名稱綁定。函數的內在名稱不在名稱檢索中起作用。在我們之前看到的例子中：

>>> f = max
>>> f
<built-in function max>

名稱max是函數的內在名稱，以及打印f時我們看到的名稱。此外，名稱max和f在全局環境中都綁定到了相同函數上。

在我們介紹 Python 的附加特性時，我們需要擴展這些圖示。每次我們這樣做的時候，我們都會列出圖示可以表達的新特性。

**新的環境特性：**賦值和用戶定義的函數定義。

1.3.2 調用用戶定義的函數

為了求出運算符為用戶定義函數的調用表達式，Python 解釋器遵循與求出運算符為內建函數的表達式相似的過程。也就是說，解釋器求出操作數表達式，並且對產生的實參調用具名函數。

調用用戶定義的函數的行為引入了第二個局部幀，它只能由函數來訪問。為了對一些實參調用用戶定義的函數：

1. 在新的局部幀中，將實參綁定到函數的形式參數上。
2. 在當前幀的開頭以及全局幀的末尾求出函數體。

函數體求值所在的環境由兩個幀組成：第一個是局部幀，包含參數綁定，之後是全局幀，包含其它所有東西。每個函數示例都有自己的獨立局部幀。

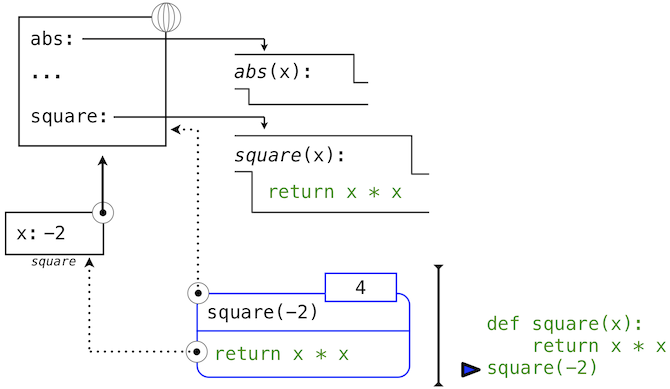
這張圖包含兩個不同的 Python 解釋器層面：當前的環境，以及表達式樹的一部分，它和要求值的代碼的當前一行相關。我們描述了調用表達式的求值，用戶定義的函數（藍色）表示為兩部分的圓角矩形。點線箭頭表示哪個環境用於在每個部分求解表達式。

• 上半部分展示了調用表達式的求值。這個調用表達式並不在任何函數里面，所以他在全局環境中求值。所以，任何裡面的名稱（例如square）都會在全局幀中檢索。
• 下半部分展示了square函數的函數體。它的返回表達式在上面的步驟1引入的新環境中求值，它將square的形式參數x的名稱綁定到實參的值-2上。

環境中幀的順序會影響由表達式中的名稱檢索返回的值。我們之前說名稱求解為當前環境中與這個名稱關聯的值。我們現在可以更精確一些：

• 名稱求解為當前環境中，最先發現該名稱的幀中，綁定到這個名稱的值。

我們關於環境、名稱和函數的概念框架建立了求值模型，雖然一些機制的細節仍舊沒有指明（例如綁定如何實現），我們的模型在描述解釋器如何求解調用表示上，變得更準確和正確。在第三章我們會看到這一模型如何用作一個藍圖來實現編程語言的可工作的解釋器。

**新的環境特性：**函數調用。

1.3.3 示例：調用用戶定義的函數

讓我們再一次考慮兩個簡單的定義：

>>> from operator import add, mul
>>> def square(x):
        return mul(x, x)
>>> def sum_squares(x, y):
        return add(square(x), square(y))

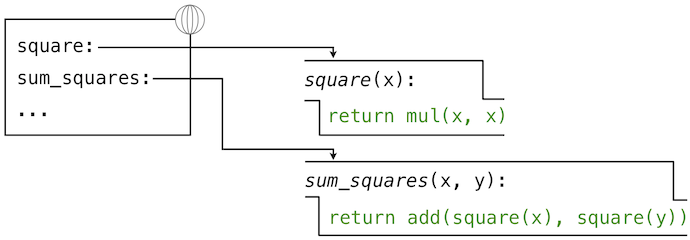
以及求解下列調用表達式的過程：

>>> sum_squares(5, 12)
169

Python 首先會求出名稱sum_squares，它在全局幀綁定了用戶定義的函數。基本的數字表達式 5 和 12 求值為它們所表達的數值。

之後，Python 調用了sum_squares，它引入了局部幀，將x綁定為 5，將y綁定為 12。

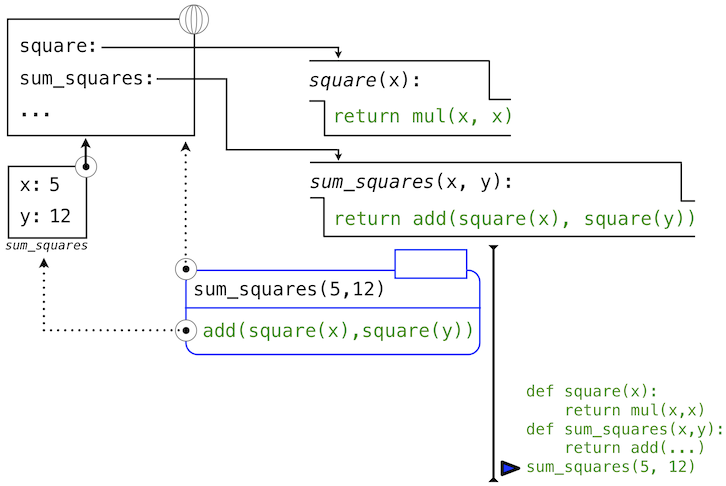
這張圖中，局部幀指向它的後繼，全局幀。所有局部幀必須指向某個先導，這些鏈接定義了當前環境中的幀序列。

sum_square的函數體包含下列調用表達式：

   add     (  square(x)  ,  square(y)  )
 ________     _________     _________
"operator"   "operand 0"   "operand 1"

全部三個子表達式在當前環境中求值，它開始於標記為sum_squares的幀。運算符字表達式add是全局幀中發現的名稱，綁定到了內建的加法函數上。兩個操作數子表達式必須在加法函數調用之前依次求值。兩個操作數都在當前環境中求值，開始於標記為sum_squares的幀。在下面的環境圖示中，我們把這一幀叫做A，並且將指向這一幀的箭頭同時替換為標籤A。

在使用這個局部幀的情況下，函數體表達式mul(x, x)求值為 25。

我們的求值過程現在輪到了操作數 1，y的值為 12。Python 再次求出square的函數體。這次引入了另一個局部環境幀，將x綁定為 12。所以，操作數 1 求值為 144。

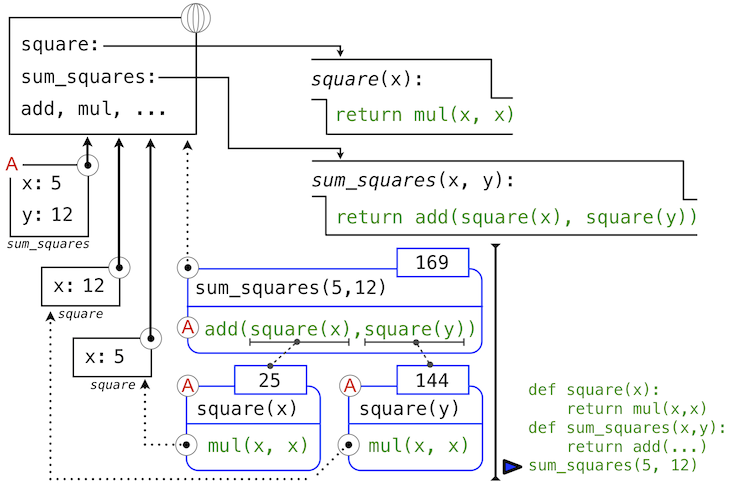
最後，對實參 25 和 144 調用加法會產生sum_squares函數體的最終值：169。

這張圖雖然複雜，但是用於展示我們目前為止發展出的許多基礎概念。名稱綁定到值上面，它延伸到許多局部幀中，局部幀在唯一的全局幀之上，全局幀包含共享名稱。表達式為樹形結構，以及每次子表達式包含用戶定義函數的調用時，環境必須被擴展。

所有這些機制的存在確保了名稱在表達式中正確的地方解析為正確的值。這個例子展示了為什麼我們的模型需要所引入的複雜性。所有三個局部幀都包含名稱x的綁定。但是這個名稱在不同的幀中綁定到了不同的值上。局部幀分離了這些名稱。

1.3.4 局部名稱

函數實現的細節之一是實現者對形式參數名稱的選擇不應影響函數行為。所以，下面的函數應具有相同的行為：

>>> def square(x):
        return mul(x, x)
>>> def square(y):
        return mul(y, y)

這個原則 -- 也就是函數應不依賴於編寫者選擇的參數名稱 -- 對編程語言來說具有重要的結果。最簡單的結果就是函數參數名稱應保留在函數體的局部範圍中。

如果參數不位於相應函數的局部範圍中，square的參數x可能和sum_squares中的參數x產生混亂。嚴格來說，這並不是問題所在：不同局部幀中的x的綁定是不相關的。我們的計算模型具有嚴謹的設計來確保這種獨立性。

我們說局部名稱的作用域被限制在定義它的用戶定義函數的函數體中。當一個名稱不能再被訪問時，它就離開了作用域。作用域的行為並不是我們模型的新事實，它是環境的工作方式的結果。

1.3.5 實踐指南：選擇名稱

可修改的名稱並不代表形式參數的名稱完全不重要。反之，選擇良好的函數和參數名稱對於函數定義的人類可解釋性是必要的。

下面的準則派生於 Python 的代碼風格指南，可被所有（非反叛）Python 程序員作為指南。一些共享的約定會使社區成員之間的溝通變得容易。遵循這些約定有一些副作用，我會發現你的代碼在內部變得一致。

1. 函數名稱應該小寫，以下劃線分隔。提倡描述性的名稱。
2. 函數名稱通常反映解釋器向參數應用的操作（例如print、add、square），或者結果（例如max、abs、sum）。
3. 參數名稱應小寫，以下劃線分隔。提倡單個詞的名稱。
4. 參數名稱應該反映參數在函數中的作用，並不僅僅是滿足的值的類型。
5. 當作用非常明確時，單個字母的參數名稱可以接受，但是永遠不要使用l（小寫的L）和O（大寫的o），或者I（大寫的i）來避免和數字混淆。

週期性對你編寫的程序複查這些準則，不用多久你的名稱會變得十分 Python 化。

1.3.6 作為抽象的函數

雖然sum_squares十分簡單，但是它演示了用戶定義函數的最強大的特性。sum_squares函數使用square函數定義，但是僅僅依賴於square定義在輸入參數和輸出值之間的關係。

我們可以編寫sum_squares，而不用考慮如何計算一個數值的平方。平方計算的細節被隱藏了，並可以在之後考慮。確實，在sum_squares看來，square並不是一個特定的函數體，而是某個函數的抽象，也就是所謂的函數式抽象。在這個層級的抽象中，任何能計算平方的函數都是等價的。

所以，僅僅考慮返回值的情況下，下面兩個計算平方的函數是難以區分的。每個都接受數值參數並且產生那個數的平方作為返回值。

>>> def square(x):
        return mul(x, x)
>>> def square(x):
        return mul(x, x-1) + x

換句話說，函數定義應該能夠隱藏細節。函數的用戶可能不能自己編寫函數，但是可以從其它程序員那裡獲得它作為“黑盒”。用戶不應該需要知道如何實現來調用。Python 庫擁有這個特性。許多開發者使用在這裡定義的函數，但是很少有人看過它們的實現。實際上，許多 Python 庫的實現並不完全用 Python 編寫，而是 C 語言。

1.3.7 運算符

算術運算符（例如+和-）在我們的第一個例子中提供了組合手段。但是我們還需要為包含這些運算符的表達式定義求值過程。

每個帶有中綴運算符的 Python 表達式都有自己的求值過程，但是你通常可以認為他們是調用表達式的快捷方式。當你看到

>>> 2 + 3
5

的時候，可以簡單認為它是

>>> add(2, 3)
5

的快捷方式。

中綴記號可以嵌套，就像調用表達式那樣。Python 運算符優先級中採用了常規的數學規則，它指導瞭如何解釋帶有多種運算符的複合表達式。

>>> 2 + 3 * 4 + 5
19

和下面的表達式的求值結果相同

>>> add(add(2, mul(3, 4)) , 5)
19

調用表達式的嵌套比運算符版本更加明顯。Python 也允許括號括起來的子表達式，來覆蓋通常的優先級規則，或者使表達式的嵌套結構更加明顯：

>>> (2 + 3) * (4 + 5)
45

和下面的表達式的求值結果相同

>>> mul(add(2, 3), add(4, 5))
45

你應該在你的程序中自由使用這些運算符和括號。對於簡單的算術運算，Python 在慣例上傾向於運算符而不是調用表達式。

1.4 實踐指南：函數的藝術

來源：1.4 Practical Guidance: The Art of the Function

譯者：飛龍

協議：CC BY-NC-SA 4.0

函數是所有程序的要素，無論規模大小，並且在編程語言中作為我們表達計算過程的主要媒介。目前為止，我們討論了函數的形式特性，以及它們如何使用。我們現在跳轉到如何編寫良好的函數這一話題。

• 每個函數都應該只做一個任務。這個任務可以使用短小的名稱來定義，使用一行文本來標識。順序執行多個任務的函數應該拆分在多個函數中。
• 不要重複勞動（DRY）是軟件工程的中心法則。所謂的DRY原則規定多個代碼段不應該描述重複的邏輯。反之，邏輯應該只實現一次，指定一個名稱，並且多次使用。如果你發現自己在複製粘貼一段代碼，你可能發現了一個使用函數抽象的機會。
• 函數應該定義得通常一些，準確來說，平方並不是在 Python 庫中，因為它是pow函數的一個特例，這個函數計算任何數的任何次方。

這些準則提升代碼的可讀性，減少錯誤數量，並且通常使編寫的代碼總數最小。將複雜的任務拆分為簡潔的函數是一個技巧，它需要一些經驗來掌握。幸運的是，Python 提供了一些特性來支持你的努力。

1.4.1 文檔字符串

函數定義通常包含描述這個函數的文檔，叫做文檔字符串，它必須在函數體中縮進。文檔字符串通常使用三個引號。第一行描述函數的任務。隨後的一些行描述參數，並且澄清函數的行為：

>>> def pressure(v, t, n):
        """Compute the pressure in pascals of an ideal gas.

        Applies the ideal gas law: http://en.wikipedia.org/wiki/Ideal_gas_law

        v -- volume of gas, in cubic meters
        t -- absolute temperature in degrees kelvin
        n -- particles of gas
        """
        k = 1.38e-23  # Boltzmann's constant
        return n * k * t / v

當你以函數名稱作為參數來調用help時，你會看到它的文檔字符串（按下q來退出 Python 幫助）。

>>> help(pressure)

編寫 Python 程序時，除了最簡單的函數之外，都要包含文檔字符串。要記住，代碼只編寫一次，但是會閱讀多次。Python 文檔包含了文檔字符串準則，它在不同的 Python 項目中保持一致。

1.4.2 參數默認值

定義普通函數的結果之一就是額外參數的引入。具有許多參數的函數調用起來非常麻煩，也難以閱讀。

在 Python 中，我們可以為函數的參數提供默認值。調用這個函數時，帶有默認值的參數是可選的。如果它們沒有提供，默認值就會綁定到形式參數的名稱上。例如，如果某個應用通常用來計算一摩爾粒子的壓強，這個值就可以設為默認：

>>> k_b=1.38e-23  # Boltzmann's constant
>>> def pressure(v, t, n=6.022e23):
        """Compute the pressure in pascals of an ideal gas.

        v -- volume of gas, in cubic meters
        t -- absolute temperature in degrees kelvin
        n -- particles of gas (default: one mole)
        """
        return n * k_b * t / v
>>> pressure(1, 273.15)
2269.974834

這裡，pressure的定義接受三個參數，但是在調用表達式中只提供了兩個。這種情況下，n的值通過def語句的默認值獲得（它看起來像對n的賦值，雖然就像這個討論暗示的那樣，更大程度上它是條件賦值）。

作為準則，用於函數體的大多數數據值應該表示為具名參數的默認值，這樣便於查看，以及被函數調用者修改。一些值永遠不會改變，就像基本常數k_b，應該定義在全局幀中。

1.5 控制

來源：1.5 Control

譯者：飛龍

協議：CC BY-NC-SA 4.0

我們現在可以定義的函數能力有限，因為我們還不知道一種方法來進行測試，並且根據測試結果來執行不同的操作。控制語句可以讓我們完成這件事。它們不像嚴格的求值子表達式那樣從左向右編寫，並且可以從它們控制解釋器下一步做什麼當中得到它們的名稱。這可能基於表達式的值。

1.5.1 語句

目前為止，我們已經初步思考了如何求出表達式。然而，我們已經看到了三種語句：賦值、def和return語句。這些 Python 代碼並不是表達式，雖然它們中的一部分是表達式。

要強調的是，語句的值是不相干的（或不存在的），我們使用執行而不是求值來描述語句。 每個語句都描述了對解釋器狀態的一些改變，執行語句會應用這些改變。像我們之前看到的return和賦值語句那樣，語句的執行涉及到求解所包含的子表達式。

表達式也可以作為語句執行，其中它們會被求值，但是它們的值會捨棄。執行純函數沒有什麼副作用，但是執行非純函數會產生效果作為函數調用的結果。

考慮下面這個例子：

>>> def square(x):
        mul(x, x) # Watch out! This call doesn't return a value.

這是有效的 Python 代碼，但是並不是想表達的意思。函數體由表達式組成。表達式本身是個有效的語句，但是語句的效果是，mul函數被調用了，然後結果被捨棄了。如果你希望對錶達式的結果做一些事情，你需要這樣做：使用賦值語句來儲存它，或者使用return語句將它返回：

>>> def square(x):
        return mul(x, x)

有時編寫一個函數體是表達式的函數是有意義的，例如調用類似print的非純函數：

>>> def print_square(x):
        print(square(x))

在最高層級上，Python 解釋器的工作就是執行由語句組成的程序。但是，許多有意思的計算工作來源於求解表達式。語句管理程序中不同表達式之間的關係，以及它們的結果會怎麼樣。

1.5.2 複合語句

通常，Python 的代碼是語句的序列。一條簡單的語句是一行不以分號結束的代碼。複合語句之所以這麼命名，因為它是其它（簡單或複合）語句的複合。複合語句一般佔據多行，並且以一行以冒號結尾的頭部開始，它標識了語句的類型。同時，一個頭部和一組縮進的代碼叫做子句（或從句）。複合語句由一個或多個子句組成。

<header>:
    <statement>
    <statement>
    ...
<separating header>:
    <statement>
    <statement>
    ...
...

我們可以這樣理解我們已經見到的語句：

• 表達式、返回語句和賦值語句都是簡單語句。
• def語句是複合語句。def頭部之後的組定義了函數體。

為每種頭部特化的求值規則指導了組內的語句什麼時候以及是否會被執行。我們說頭部控制語句組。例如，在def語句的例子中，我們看到返回表達式並不會立即求值，而是儲存起來用於以後的使用，當所定義的函數最終調用時就會求值。

我們現在也能理解多行的程序了。

• 執行語句序列需要執行第一條語句。如果這個語句不是重定向控制，之後執行語句序列的剩餘部分，如果存在的話。

這個定義揭示出遞歸定義“序列”的基本結構：一個序列可以劃分為它的第一個元素和其餘元素。語句序列的“剩餘”部分也是一個語句序列。所以我們可以遞歸應用這個執行規則。這個序列作為遞歸數據結構的看法會在隨後的章節中再次出現。

這一規則的重要結果就是語句順序執行，但是隨後的語句可能永遠不會執行到，因為有重定向控制。

**實踐指南：**在縮進代碼組時，所有行必須以相同數量以及相同方式縮進（空格而不是Tab）。任何縮進的變動都會導致錯誤。

1.5.3 定義函數 II：局部賦值

一開始我們說，用戶定義函數的函數體只由帶有一個返回表達式的一個返回語句組成。實際上，函數可以定義為操作的序列，不僅僅是一條表達式。Python 複合語句的結構自然讓我們將函數體的概念擴展為多個語句。

無論用戶定義的函數何時被調用，定義中的子句序列在局部環境內執行。return語句會重定向控制：無論什麼時候執行return語句，函數調用的流程都會中止，返回表達式的值會作為被調用函數的返回值。

於是，賦值語句現在可以出現在函數體中。例如，這個函數以第一個數的百分數形式，返回兩個數量的絕對值，並使用了兩步運算：

>>> def percent_difference(x, y):
        difference = abs(x-y)
        return 100 * difference / x
>>> percent_difference(40, 50)
25.0

賦值語句的效果是在當前環境的第一個幀上，將名字綁定到值上。於是，函數體內的賦值語句不會影響全局幀。函數只能操作局部作用域的現象是創建模塊化程序的關鍵，其中純函數只通過它們接受和返回的值與外界交互。

當然，percent_difference函數也可以寫成一個表達式，就像下面這樣，但是返回表達式會更加複雜：

>>> def percent_difference(x, y):
        return 100 * abs(x-y) / x

目前為止，局部賦值並不會增加函數定義的表現力。當它和控制語句組合時，才會這樣。此外，局部賦值也可以將名稱賦為間接量，在理清複雜表達式的含義時起到關鍵作用。

**新的環境特性：**局部賦值。

1.5.4 條件語句

Python 擁有內建的絕對值函數：

>>> abs(-2)
2

我們希望自己能夠實現這個函數，但是我們當前不能直接定義函數來執行測試並做出選擇。我們希望表達出，如果x是正的，abs(x)返回x，如果x是 0，abx(x)返回 0，否則abs(x)返回-x。Python 中，我們可以使用條件語句來表達這種選擇。

>>> def absolute_value(x):
        """Compute abs(x)."""
        if x > 0:
            return x
        elif x == 0:
            return 0
        else:
            return -x
            
>>> absolute_value(-2) == abs(-2)
True

absolute_value的實現展示了一些重要的事情：

**條件語句。**Python 中的條件語句包含一系列的頭部和語句組：一個必要的if子句，可選的elif子句序列，和最後可選的else子句：

if <expression>:
    <suite>
elif <expression>:
    <suite>
else:
    <suite>

當執行條件語句時，每個子句都按順序處理：

1. 求出頭部中的表達式。
2. 如果它為真，執行語句組。之後，跳過條件語句中隨後的所有子句。

如果能到達else子句（僅當所有if和elif表達式值為假時），它的語句組才會被執行。

**布爾上下文。**上面過程的執行提到了“假值”和“真值”。條件塊頭部語句中的表達式也叫作布爾上下文：它們值的真假對控制流很重要，但在另一方面，它們的值永遠不會被賦值或返回。Python 包含了多種假值，包括 0、None和布爾值False。所有其他數值都是真值。在第二章中，我們就會看到每個 Python 中的原始數據類型都是真值或假值。

**布爾值。**Python 有兩種布爾值，叫做True和False。布爾值表示了邏輯表達式中的真值。內建的比較運算符，>、<、>=、<=、==、!=，返回這些值。

>>> 4 < 2
False
>>> 5 >= 5
True

第二個例子讀作“5 大於等於 5”，對應operator模塊中的函數ge。

>>> 0 == -0
True

最後的例子讀作“0 等於 -0”，對應operator模塊的eq函數。要注意 Python 區分賦值（=）和相等測試（==）。許多語言中都有這個慣例。

**布爾運算符。**Python 也內建了三個基本的邏輯運算符：

>>> True and False
False
>>> True or False
True
>>> not False
True

邏輯表達式擁有對應的求值過程。這些過程揭示了邏輯表達式的真值有時可以不執行全部子表達式而確定，這個特性叫做短路。

為了求出表達式<left> and <right>：

1. 求出子表達式<left>。
2. 如果結果v是假值，那麼表達式求值為v。
3. 否則表達式的值為子表達式<right>。

為了求出表達式<left> or <right>：

1. 求出子表達式<left>。
2. 如果結果v是真值，那麼表達式求值為v。
3. 否則表達式的值為子表達式<right>。

為了求出表達式not <exp>：

1. 求出<exp>，如果值是True那麼返回值是假值，如果為False則反之。

這些值、規則和運算符向我們提供了一種組合測試結果的方式。執行測試以及返回布爾值的函數通常以is開頭，並不帶下劃線（例如isfinite、isdigit、isinstance等等）。

1.5.5 迭代

除了選擇要執行的語句，控制語句還用於表達重複操作。如果我們編寫的每一行代碼都只執行一次，程序會變得非常沒有生產力。只有通過語句的重複執行，我們才可以釋放計算機的潛力，使我們更加強大。我們已經看到了重複的一種形式：一個函數可以多次調用，雖然它只定義一次。迭代控制結構是另一種將相同語句執行多次的機制。

考慮斐波那契數列，其中每個數值都是前兩個的和：

0, 1, 1, 2, 3, 5, 8, 13, 21, ...

每個值都通過重複使用“前兩個值的和”的規則構造。為了構造第 n 個值，我們需要跟蹤我們創建了多少個值（k），以及第 k 個值（curr）和它的上一個值（pred），像這樣：

>>> def fib(n):
        """Compute the nth Fibonacci number, for n >= 2."""
        pred, curr = 0, 1   # Fibonacci numbers
        k = 2               # Position of curr in the sequence
        while k < n:
            pred, curr = curr, pred + curr  # Re-bind pred and curr
            k = k + 1                       # Re-bind k
        return curr
>>> fib(8)
13

要記住逗號在賦值語句中分隔了多個名稱和值。這一行：

pred, curr = curr, pred + curr

具有將curr的值重新綁定到名稱pred上，以及將pred + curr的值重新綁定到curr上的效果。所有=右邊的表達式會在綁定發生之前求出來。

while子句包含一個頭部表達式，之後是語句組：

while <expression>:
    <suite>

為了執行while子句：

1. 求出頭部表達式。
2. 如果它為真，執行語句組，之後返回到步驟 1。

在步驟 2 中，整個while子句的語句組在頭部表達式再次求值之前被執行。

為了防止while子句的語句組無限執行，它應該總是在每次通過時修改環境的狀態。

不終止的while語句叫做無限循環。按下<Control>-C可以強制讓 Python 停止循環。

1.5.6 實踐指南：測試

函數的測試是驗證函數的行為是否符合預期的操作。我們的函數現在已經足夠複雜了，我們需要開始測試我們的實現。

測試是系統化執行這個驗證的機制。測試通常寫為另一個函數，這個函數包含一個或多個被測函數的樣例調用。返回值之後會和預期結果進行比對。不像大多數通用的函數，測試涉及到挑選特殊的參數值，並使用它來驗證調用。測試也可作為文檔：它們展示瞭如何調用函數，以及什麼參數值是合理的。

要注意我們也將“測試”這個詞用於if或while語句的頭部中作為一種技術術語。當我們將“測試”這個詞用作表達式，或者用作一種驗證機制時，它應該在語境中十分明顯。

**斷言。**程序員使用assert語句來驗證預期，例如測試函數的輸出。assert語句在布爾上下文中只有一個表達式，後面是帶引號的一行文本（單引號或雙引號都可以，但是要一致）如果表達式求值為假，它就會顯示。

>>> assert fib(8) == 13, 'The 8th Fibonacci number should be 13'

當被斷言的表達式求值為真時，斷言語句的執行沒有任何效果。當它是假時，asset會造成執行中斷。

為fib編寫的test函數測試了幾個參數，包含n的極限值：

>>> def fib_test():
        assert fib(2) == 1, 'The 2nd Fibonacci number should be 1'
        assert fib(3) == 1, 'The 3nd Fibonacci number should be 1'
        assert fib(50) == 7778742049, 'Error at the 50th Fibonacci number'

在文件中而不是直接在解釋器中編寫 Python 時，測試可以寫在同一個文件，或者後綴為_test.py的相鄰文件中。

**Doctest。**Python 提供了一個便利的方法，將簡單的測試直接寫到函數的文檔字符串內。文檔字符串的第一行應該包含單行的函數描述，後面是一個空行。參數和行為的詳細描述可以跟隨在後面。此外，文檔字符串可以包含調用該函數的簡單交互式會話：

>>> def sum_naturals(n):
        """Return the sum of the first n natural numbers

        >>> sum_naturals(10)
        55
        >>> sum_naturals(100)
        5050
        """
        total, k = 0, 1
        while k <= n:
          total, k = total + k, k + 1
        return total

之後，可以使用 doctest 模塊來驗證交互。下面的globals函數返回全局變量的表示，解釋器需要它來求解表達式。

>>> from doctest import run_docstring_examples
>>> run_docstring_examples(sum_naturals, globals())

在文件中編寫 Python 時，可以通過以下面的命令行選項啟動 Python 來運行一個文檔中的所有 doctest。

python3 -m doctest <python_source_file>

高效測試的關鍵是在實現新的函數之後（甚至是之前）立即編寫（以及執行）測試。只調用一個函數的測試叫做單元測試。詳盡的單元測試是良好程序設計的標誌。

1.6 高階函數

來源：1.6 Higher-Order Functions

譯者：飛龍

協議：CC BY-NC-SA 4.0

我們已經看到，函數實際上是描述複合操作的抽象，這些操作不依賴於它們的參數值。在square中，

>>> def square(x):
        return x * x

我們不會談論特定數值的平方，而是一個獲得任何數值平方的方法。當然，我們可以不定義這個函數來使用它，通過始終編寫這樣的表達式：

>>> 3 * 3
9
>>> 5 * 5
25

並且永遠不會顯式提及square。這種實踐適合類似square的簡單操作。但是對於更加複雜的操作會變得困難。通常，缺少函數定義會對我們非常不利，它會強迫我們始終工作在特定操作的層級上，這在語言中非常原始（這個例子中是乘法），而不是高級操作。我們應該從強大的編程語言索取的東西之一，是通過將名稱賦為常用模式來構建抽象的能力，以及之後直接使用抽象的能力。函數提供了這種能力。

我們將會在下個例子中看到，代碼中會反覆出現一些常見的編程模式，但是使用一些不同函數來實現。這些模式也可以被抽象和給予名稱。

為了將特定的通用模式表達為具名概念，我們需要構造可以接受其他函數作為參數的函數，或者將函數作為返回值的函數。操作函數的函數叫做高階函數。這一節展示了高階函數可用作強大的抽象機制，極大提升語言的表現力。

1.6.1 作為參數的函數

考慮下面三個函數，它們都計算總和。第一個，sum_naturals，計算截至n的自然數的和：

>>> def sum_naturals(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total
>>> sum_naturals(100)
5050

第二個，sum_cubes，計算截至n的自然數的立方和：

>>> def sum_cubes(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + pow(k, 3), k + 1
        return total
>>> sum_cubes(100)
25502500

第三個，計算這個級數中式子的和：

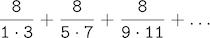
它會慢慢收斂於pi。

>>> def pi_sum(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + 8 / (k * (k + 2)), k + 4
        return total
>>> pi_sum(100)
3.121594652591009

這三個函數在背後都具有相同模式。它們大部分相同，只是名字、用於計算被加項的k的函數，以及提供k的下一個值的函數不同。我們可以通過向相同的模板中填充槽位來生成每個函數：

def <name>(n):
    total, k = 0, 1
    while k <= n:
        total, k = total + <term>(k), <next>(k)
    return total

這個通用模板的出現是一個強有力的證據，證明有一個實用抽象正在等著我們表現出來。這些函數的每一個都是式子的求和。作為程序的設計者，我們希望我們的語言足夠強大，便於我們編寫函數來自我表達求和的概念，而不僅僅是計算特定和的函數。我們可以在 Python 中使用上面展示的通用模板，並且把槽位變成形式參數來輕易完成它。

>>> def summation(n, term, next):
        total, k = 0, 1
        while k <= n:
            total, k = total + term(k), next(k)
        return total

要注意summation接受上界n，以及函數term和next作為參數。我們可以像任何函數那樣使用summation，它簡潔地表達了求和。

>>> def cube(k):
        return pow(k, 3)
>>> def successor(k):
        return k + 1
>>> def sum_cubes(n):
        return summation(n, cube, successor)
>>> sum_cubes(3)
36

使用identity 函數來返回參數自己，我們就可以對整數求和：

>>> def identity(k):
        return k
>>> def sum_naturals(n):
        return summation(n, identity, successor)
>>> sum_naturals(10)
55

我們也可以逐步定義pi_sum，使用我們的summation抽象來組合組件。

>>> def pi_term(k):
        denominator = k * (k + 2)
        return 8 / denominator
>>> def pi_next(k):
        return k + 4
>>> def pi_sum(n):
        return summation(n, pi_term, pi_next)
>>> pi_sum(1e6)
3.1415906535898936

1.6.2 作為一般方法的函數

我們引入的用戶定義函數作為一種數值運算的抽象模式，便於使它們獨立於涉及到的特定數值。使用高階函數，我們開始尋找更強大的抽象類型：一些函數表達了計算的一般方法，獨立於它們調用的特定函數。

儘管函數的意義在概念上擴展了，我們對於如何求解調用表達式的環境模型也優雅地延伸到了高階函數，沒有任何改變。當一個用戶定義函數以一些實參調用時，形式參數會在最新的局部幀中綁定實參的值（它們可能是函數）。

考慮下面的例子，它實現了迭代改進的一般方法，並且可以用於計算黃金比例。迭代改進算法以一個方程的解的guess（推測值）開始。它重複調用update函數來改進這個推測值，並且調用test來檢查是否當前的guess“足夠接近”所認為的正確值。

>>> def iter_improve(update, test, guess=1):
        while not test(guess):
            guess = update(guess)
        return guess

test函數通常檢查兩個函數f和g在guess值上是否彼此接近。測試f(x)是否接近於g(x)也是計算的一般方法。

>>> def near(x, f, g):
        return approx_eq(f(x), g(x))

程序中測試相似性的一個常見方式是將數值差的絕對值與一個微小的公差值相比：

>>> def approx_eq(x, y, tolerance=1e-5):
        return abs(x - y) < tolerance

黃金比例，通常叫做phi，是經常出現在自然、藝術、和建築中的數值。它可以通過iter_improve使用golden_update來計算，並且在它的後繼等於它的平方時收斂。

>>> def golden_update(guess):
        return 1/guess + 1
>>> def golden_test(guess):
        return near(guess, square, successor)

這裡，我們已經向全局幀添加了多個綁定。函數值的描述為了簡短而有所刪節：

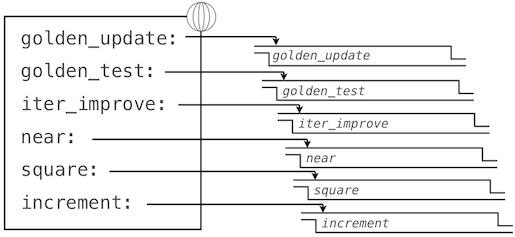
使用golden_update和golden_test參數來調用iter_improve會計算出黃金比例的近似值。

>>> iter_improve(golden_update, golden_test)
1.6180371352785146

通過跟蹤我們的求值過程的步驟，我們就可以觀察結果如何計算。首先，iter_improve的局部幀以update、test和guess構建。在iter_improve的函數體中，名稱test綁定到golden_test上，它在初始值guess上調用。之後，golden_test調用near，創建第三個局部幀，它將形式參數f和g綁定到square和successor上。

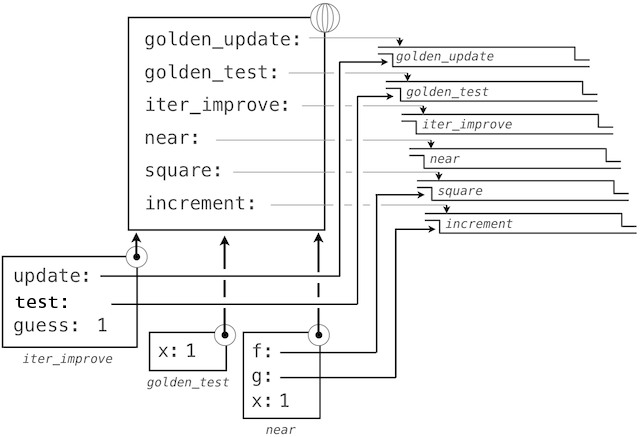
完成near的求值之後，我們看到golden_test為False，因為 1 並不非常接近於 2。所以，while子句代碼組內的求值過程，以及這個機制的過程會重複多次。

這個擴展後的例子展示了計算機科學中兩個相關的重要概念。首先，命名和函數允許我們抽象而遠離大量的複雜性。當每個函數定義不重要時，由求值過程觸發的計算過程是相當複雜的，並且我們甚至不能展示所有東西。其次，基於事實，我們擁有了非常通用的求值過程，小的組件組合在複雜的過程中。理解這個過程便於我們驗證和檢查我們創建的程序。

像通常一樣，我們的新的一般方法iter_improve需要測試來檢查正確性。黃金比例可以提供這樣一個測試，因為它也有一個閉式解，我們可以將它與迭代結果進行比較。

>>> phi = 1/2 + pow(5, 1/2)/2
>>> def near_test():
        assert near(phi, square, successor), 'phi * phi is not near phi + 1'
>>> def iter_improve_test():
        approx_phi = iter_improve(golden_update, golden_test)
        assert approx_eq(phi, approx_phi), 'phi differs from its approximation'

**新的環境特性：**高階函數。

**附加部分：**我們在測試的證明中遺漏了一步。求出公差值e的範圍，使得如果tolerance為e的near(x, square, successor)值為真，那麼使用相同公差值的approx_eq(phi, x)值為真。

1.6.3 定義函數 III：嵌套定義

上面的例子演示了將函數作為參數傳遞的能力如何提高了編程語言的表現力。每個通用的概念或方程都能映射為自己的小型函數，這一方式的一個負面效果是全局幀會被小型函數弄亂。另一個問題是我們限制於特定函數的簽名：iter_improve 的update參數必須只接受一個參數。Python 中，嵌套函數的定義解決了這些問題，但是需要我們重新修改我們的模型。

讓我們考慮一個新問題：計算一個數的平方根。重複調用下面的更新操作會收斂於x的平方根：

>>> def average(x, y):
        return (x + y)/2
>>> def sqrt_update(guess, x):
        return average(guess, x/guess)

這個帶有兩個參數的更新函數和iter_improve不兼容，並且它只提供了一個介值。我們實際上只關心最後的平方根。這些問題的解決方案是把函數放到其他定義的函數體中。

>>> def square_root(x):
        def update(guess):
            return average(guess, x/guess)
        def test(guess):
            return approx_eq(square(guess), x)
        return iter_improve(update, test)

就像局部賦值，局部的def語句僅僅影響當前的局部幀。這些函數僅僅當square_root求值時在作用域內。和求值過程一致，局部的def語句在square_root調用之前並不會求值。

**詞法作用域。**局部定義的函數也可以訪問它們定義所在作用域的名稱綁定。這個例子中，update引用了名稱x，它是外層函數square_root的一個形參。這種在嵌套函數中共享名稱的規則叫做詞法作用域。嚴格來說，內部函數能夠訪問定義所在環境（而不是調用所在位置）的名稱。

我們需要兩個對我們環境的擴展來兼容詞法作用域。

1. 每個用戶定義的函數都有一個關聯環境：它的定義所在的環境。
2. 當一個用戶定義的函數調用時，它的局部幀擴展於函數所關聯的環境。

回到square_root，所有函數都在全局環境中定義，所以它們都關聯到全局環境，當我們求解square_root的前兩個子句時，我們創建了關聯到局部環境的函數。在

>>> square_root(256)
16.00000000000039

的調用中，環境首先添加了square_root的局部幀，並且求出def語句update和test（只展示了update）：

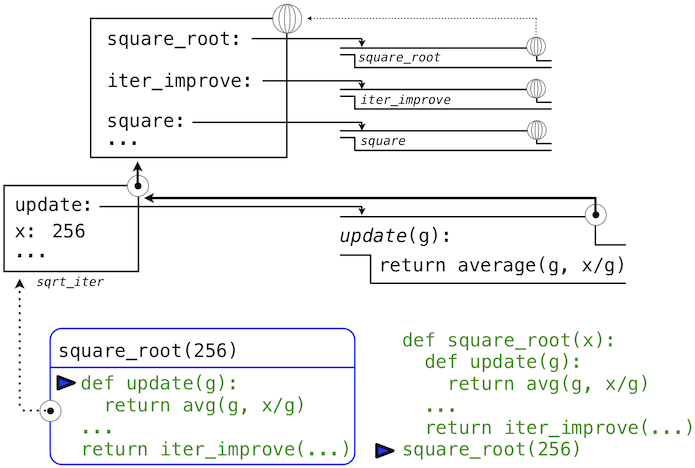
隨後，update的名稱解析到這個新定義的函數上，它是向iter_improve傳入的參數。在iter_improve的函數體中，我們必須以初始值 1 調用update函數。最後的這個調用以一開始只含有g的局部幀創建了update的環境，但是之前的square_root幀上仍舊含有x的綁定。

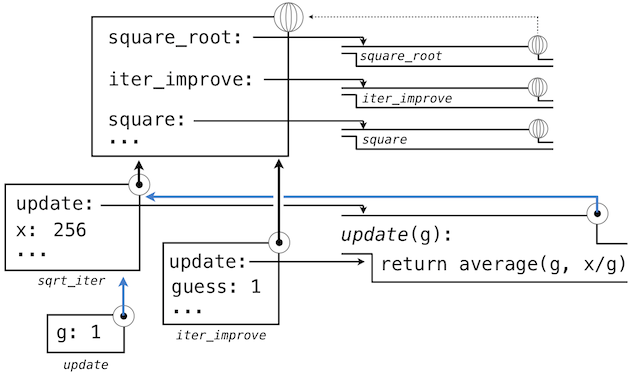
這個求值過程中，最重要的部分是函數所關聯的環境變成了局部幀，它是函數求值的地方。這個改變在圖中以藍色箭頭高亮。

以這種方式，update的函數體能夠解析名稱x。所以我們意識到了詞法作用域的兩個關鍵優勢。

• 局部函數的名稱並不影響定義所在函數外部的名稱，因為局部函數的名稱綁定到了定義處的當前局部環境中，而不是全局環境。
• 局部函數可以訪問外層函數的環境。這是因為局部函數的函數體的求值環境擴展於定義處的求值環境。

update函數自帶了一些數據：也就是在定義處環境中的數據。因為它以這種方式封裝信息，局部定義的函數通常叫做閉包。

**新的環境特性：**局部函數定義。

1.6.4 作為返回值的函數

我們的程序可以通過創建返回值是它們本身的函數，獲得更高的表現力。帶有詞法作用域的編程語言的一個重要特性就是，局部定義函數在它們返回時仍舊持有所關聯的環境。下面的例子展示了這一特性的作用。

在定義了許多簡單函數之後，composition是包含在我們的編程語言中的自然組合法。也就是說，提供兩個函數f(x)和g(x)，我們可能希望定義h(x) = f(g(x))。我們可以使用現有工具來定義複合函數：

>>> def compose1(f, g):
        def h(x):
            return f(g(x))
        return h
>>> add_one_and_square = compose1(square, successor)
>>> add_one_and_square(12)
169

compose1中的1表明複合函數和返回值都只接受一個參數。這種命名慣例並不由解釋器強制，1只是函數名稱的一部分。

這裡，我們開始觀察我們在計算的複雜模型中投入的回報。我們的環境模型不需要任何修改就能支持以這種方式返回函數的能力。

1.6.5 Lambda 表達式

目前為止，每次我們打算定義新的函數時，我們都會給它一個名稱。但是對於其它類型的表達式，我們不需要將一個間接產物關聯到名稱上。也就是說，我們可以計算a*b + c*d，而不需要給子表達式a*b或c*d，或者整個表達式來命名。Python 中，我們可以使用 Lambda 表達式憑空創建函數，它會求值為匿名函數。Lambda 表達式是函數體具有單個返回表達式的函數，不允許出現賦值和控制語句。

Lambda 表達式十分受限：它們僅僅可用於簡單的單行函數，求解和返回一個表達式。在它們適用的特殊情形中，Lambda 表達式具有強大的表現力。

>>> def compose1(f,g):
        return lambda x: f(g(x))

我們可以通過構造相應的英文語句來理解 Lambda 表達式：

     lambda            x            :          f(g(x))
"A function that    takes x    and returns     f(g(x))"

一些程序員發現使用 Lambda 表達式作為匿名函數非常簡短和直接。但是，複合的 Lambda 表達式非常難以辨認，儘管它們很簡潔。下面的定義是是正確的，但是許多程序員不能很快地理解它：

>>> compose1 = lambda f,g: lambda x: f(g(x))

通常，Python 的代碼風格傾向於顯式的def語句而不是 Lambda 表達式，但是允許它們在簡單函數作為參數或返回值的情況下使用。

這種風格規範不是準則，你可以想怎麼寫就怎麼寫，但是，在你編寫程序時，要考慮某一天可能會閱讀你的程序的人們。如果你可以讓你的程序更易於理解，你就幫了人們一個忙。

Lambda 的術語是一個歷史的偶然結果，來源於手寫的數學符號和早期打字系統限制的不兼容。

使用 lambda 來引入過程或函數看起來是不正當的。這個符號要追溯到 Alonzo Church，他在 20 世紀 30 年代開始使用“帽子”符號；他把平方函數記為ŷ . y × y。但是失敗的打字員將這個帽子移到了參數左邊，並且把它改成了大寫的 lambda：Λy . y × y；之後大寫的 lambda 就變成了小寫，現在我們就會在數學書裡看到λy . y × y，以及在 Lisp 裡看到(lambda (y) (* y y))。

-- Peter Norvig (norvig.com/lispy2.html)

儘管它的詞源不同尋常，Lambda 表達式和函數調用相應的形式語言，以及 Lambda 演算都成為了計算機科學概念的基礎，並在 Python 編程社區廣泛傳播。當我們學習解釋器的設計時，我們將會在第三章中重新碰到這個話題。

1.6.6 示例：牛頓法

最後的擴展示例展示了函數值、局部定義和 Lambda 表達式如何一起工作來簡明地表達通常的概念。

牛頓法是一個傳統的迭代方法，用於尋找使數學函數返回值為零的參數。這些值叫做一元數學函數的根。尋找一個函數的根通常等價於求解一個相關的數學方程。

• 16 的平方根是滿足square(x) - 16 = 0的x值。
• 以 2 為底 32 的對數（例如 2 與某個指數的冪為 32）是滿足pow(2, x) - 32 = 0的x值。

所以，求根的通用方法會向我們提供算法來計算平方根和對數。而且，我們想要計算根的等式只包含簡單操作：乘法和乘方。

在我們繼續之前有個註解：我們知道如何計算平方根和對數，這個事實很容易當做自然的事情。並不只是 Python，你的手機和計算機，可能甚至你的手錶都可以為你做這件事。但是，學習計算機科學的一部分是弄懂這些數如何計算，而且，這裡展示的通用方法可以用於求解大量方程，而不僅僅是內建於 Python 的東西。

在開始理解牛頓法之前，我們可以開始編程了。這就是函數抽象的威力。我們簡單地將之前的語句翻譯成代碼：

>>> def square_root(a):
        return find_root(lambda x: square(x) - a)
>>> def logarithm(a, base=2):
        return find_root(lambda x: pow(base, x) - a)

當然，在我們定義find_root之前，現在還不能調用任何函數，所以我們需要理解牛頓法如何工作。

牛頓法也是一個迭代改進算法：它會改進任何可導函數的根的推測值。要注意我們感興趣的兩個函數都是平滑的。對於

• f(x) = square(x) - 16（細線）
• f(x) = pow(2, x) - 32（粗線）

在二維平面上畫出x對f(x)的圖像，它展示了兩個函數都產生了光滑的曲線，它們在某個點穿過了 0。

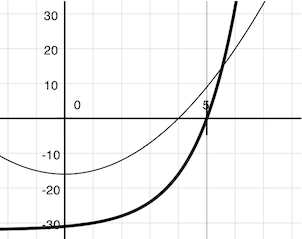
由於它們是光滑的（可導的），這些曲線可以通過任何點上的直線來近似。牛頓法根據這些線性的近似值來尋找函數的根。

想象經過點(x, f(x))的一條直線，它與函數f(x)的曲線在這一點的斜率相同。這樣的直線叫做切線，它的斜率叫做f在x上的導數。

這條直線的斜率是函數值改變量與函數參數改變量的比值。所以，按照f(x)除以這個斜率來平移x，就會得到切線到達 0 時的x值。

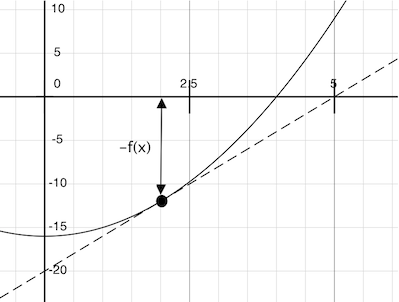
我們的牛頓更新操作表達了跟隨這條切線到零的計算過程。我們通過在非常小的區間上計算函數斜率來近似得到函數的導數。

>>> def approx_derivative(f, x, delta=1e-5):
        df = f(x + delta) - f(x)
        return df/delta
>>> def newton_update(f):
        def update(x):
            return x - f(x) / approx_derivative(f, x)
        return update

最後，我們可以定義基於newton_update（我們的迭代改進算法）的find_root函數，以及一個測試來觀察f(x)是否接近於 0。我們提供了一個較大的初始推測值來提升logarithm的性能。

>>> def find_root(f, initial_guess=10):
        def test(x):
            return approx_eq(f(x), 0)
        return iter_improve(newton_update(f), test, initial_guess)
>>> square_root(16)
4.000000000026422
>>> logarithm(32, 2)
5.000000094858201

當你實驗牛頓法時，要注意它不總是收斂的。iter_improve的初始推測值必須足夠接近於根，而且函數必須滿足各種條件。雖然具有這些缺陷，牛頓法是一個用於解決微分方程的強大的通用計算方法。實際上，非常快速的對數算法和大整數除法也採用這個技巧的變體。

1.6.7 抽象和一等函數

這一節的開始，我們以觀察用戶定義函數作為關鍵的抽象技巧，因為它們讓我們能夠將計算的通用方法表達為編程語言中的顯式元素。現在我們已經看到了高階函數如何讓我們操作這些通用方法來進一步創建抽象。

作為程序員，我們應該留意識別程序中低級抽象的機會，在它們之上構建，並泛化它們來創建更加強大的抽象。這並不是說，一個人應該總是儘可能以最抽象的方式來編程；專家級程序員知道如何選擇合適於他們任務的抽象級別。但是能夠基於這些抽象來思考，以便我們在新的上下文中能使用它們十分重要。高階函數的重要性是，它允許我們更加明顯地將這些抽象表達為編程語言中的元素，使它們能夠處理其它的計算元素。

通常，編程語言會限制操作計算元素的途徑。帶有最少限制的元素被稱為具有一等地位。一些一等元素的“權利和特權”是：

1. 它們可以綁定到名稱。
2. 它們可以作為參數向函數傳遞。
3. 它們可以作為函數的返回值返回。
4. 它們可以包含在數據結構中。

Python 總是給予函數一等地位，所產生的表現力的收益是巨大的。另一方面，控制結構不能做到：你不能像使用sum那樣將if傳給一個函數。

1.6.8 函數裝飾器

Python 提供了特殊的語法，將高階函數用作執行def語句的一部分，叫做裝飾器。

>>> def trace1(fn):
        def wrapped(x):
            print('-> ', fn, '(', x, ')')
            return fn(x)
        return wrapped
>>> @trace1
    def triple(x):
        return 3 * x
>>> triple(12)
->  <function triple at 0x102a39848> ( 12 )
36

這個例子中，定義了高階函數trace1，它返回一個函數，這個函數在調用它的參數之前執行print語句來輸出參數。triple的def語句擁有一個註解，@trace1，它會影響def的執行規則。像通常一樣，函數triple被創建了，但是，triple的名稱並沒有綁定到這個函數上，而是綁定到了在新定義的函數triple上調用trace1的返回函數值上。在代碼中，這個裝飾器等價於：

>>> def triple(x):
        return 3 * x
>>> triple = trace1(triple)

**附加部分：**實際規則是，裝飾器符號@可以放在表達式前面（@trace1僅僅是一個簡單的表達式，由單一名稱組成）。任何產生合適的值的表達式都可以。例如，使用合適的值，你可以定義裝飾器check_range，使用@check_range(1, 10)來裝飾函數定義，這會檢查函數的結果來確保它們是 1 到 10 的整數。調用check_range(1,10)會返回一個函數，之後它會用在新定義的函數上，在新定義的函數綁定到def語句中的名稱之前。感興趣的同學可以閱讀 Ariel Ortiz 編寫的一篇裝飾器的簡短教程來了解更多的例子。

第二章 使用對象構建抽象

2.1 引言

來源：2.1 Introduction

譯者：飛龍

協議：CC BY-NC-SA 4.0

在第一章中，我們專注於計算過程，以及程序設計中函數的作用。我們看到了如何使用原始數據（數值）和原始操作（算術運算），如何通過組合和控制來形成複合函數，以及如何通過給予過程名稱來創建函數抽象。我們也看到了高階函數通過操作通用計算方法來提升語言的威力。這是編程的本質。

這一章會專注於數據。數據允許我們通過使用已經獲得的計算工具，表示和操作與世界有關的信息。脫離數據結構的編程可能會滿足於探索數學特性，但是真實世界的情況，比如文檔、關係、城市和氣候模式，都擁有複雜的結構，它最好使用複合數據類型來表現。歸功於互聯網的高速發展，關於世界的大量結構信息可以免費從網上獲得。

2.1.1 對象隱喻

在這門課的開始，我們區分了函數和數據：函數執行操作，而數據被操作。當我們在數據中包含函數值時，我們承認數據也擁有行為。函數可以像數據一樣被操作，但是也可以被調用來執行計算。

在這門課中，對象作為我們對數據值的核心編程隱喻，它同樣擁有行為。對象表示信息，但是同時和它們所表示的抽象概念行為一致。對象如何和其它對象交互的邏輯，和編碼對象值的信息綁定在一起。在打印對象時，它知道如何以字母和數字把自己拼寫出來。如果一個對象由幾部分組成，它知道如何按照要求展示這些部分。對象既是信息也是過程，它們綁定在一起來展示覆雜事物的屬性、交互和行為。

Python 中所實現的對象隱喻具有特定的對象語法和相關的術語，我們會使用示例來介紹。日期（date）就是一種簡單對象。

>>> from datetime import date

date的名字綁定到了一個類上面。類表示一類對象。獨立的日期叫做這個類的實例，它們可以通過像函數那樣在參數上調用這個類來構造，這些參數描述了實例。

>>> today = date(2011, 9, 12)

雖然today從原始數值中構造，它的行為就像日期那樣。例如，將它與另一個日期相減會得到時間差，它可以通過調用str來展示為一行文本：

>>> str(date(2011, 12, 2) - today)
'81 days, 0:00:00'

對象擁有屬性，它們是帶有名字的值，也是對象的一部分。Python 中，我們使用點運算符來訪問對象屬性：

<expression> . <name>

上面的<expression>求值為對象，<name>是對象的某個屬性名稱。

不像我們之前見過的名稱，這些屬性名稱在一般的環境中不可用。反之，屬性名稱是點運算符之前的對象實例的特定部分。

>>> today.year
2011

對象也擁有方法，它是值為函數的屬性。在隱喻上，對象“知道”如何執行這些方法。方法從它們的參數和對象中計算出它們的結果。例如，today的strftime方法接受一個指定如何展示日期的參數（例如%A表示星期幾應該以全稱拼寫）。

>>> today.strftime('%A, %B %d')
'Monday, September 12'

計算strftime的返回值需要兩個輸入：描述輸出格式的字符串，以及綁定到today的日期信息。這個方法使用日期特定的邏輯來產生結果。我們從不會說 2011 年九月十二日是星期一，但是知道一個人的工作日是日期的一部分。通過綁定行為和信息，Python 對象提供了可靠、獨立的日期抽象。

點運算符在 Python 中提供了另一種組合表達式。點運算符擁有定義好的求值過程。但是，點運算符如何求值的精確解釋，要等到我們引入面向對象編程的完整範式，在幾節之後。

即使我們還不能精確描述對象如何工作，我們還是可以開始將數據看做對象，因為 Python 中萬物皆對象。

2.1.2 原始數據類型

Python 中每個對象都擁有一個類型。type函數可以讓我們查看對象的類型。

>>> type(today)
<class 'datetime.date'>

目前為止，我們學過的對象類型只有數值、函數、布爾值和現在的日期。我們也碰到了集合和字符串，但是需要更深入地學習它們。有許多其它的對象類型 -- 聲音、圖像、位置、數據連接等等 -- 它們的多數可以通過組合和抽象的手段來定義，我們在這一章會研究它們。Python 只有一小部分內建於語言的原始或原生數據類型。

原始數據類型具有以下特性：

1. 原始表達式可以計算這些類型的對象，叫做字面值。
2. 內建的函數、運算符和方法可以操作這些對象。

像我們看到的那樣，數值是原始類型，數字字面值求值為數值，算術運算符操作數值對象：

>>> 12 + 3000000000000000000000000
3000000000000000000000012

實際上，Python 包含了三個原始數值類型：整數（int）、實數（float）和複數（complex）。

>>> type(2)
<class 'int'>
>>> type(1.5)
<class 'float'>
>>> type(1+1j)
<class 'complex'>

名稱float來源於實數在 Python 中表示的方式：“浮點”表示。雖然數值表示的細節不是這門課的話題，一些int和float對象的高層差異仍然很重要。特別是，int對象只能表示整數，但是表示得更精確，不帶有任何近似。另一方面，float對象可以表示很大範圍內的分數，但是不能表示所有有理數。然而，浮點對象通常用於近似表示實數和有理數，舍入到某個有效數字的數值。

**擴展閱讀。**下面的章節介紹了更多的 Python 原始數據類型，專注於它們在創建實用數據抽象中的作用。Dive Into Python 3 中的原始數據類型一章提供了所有 Python 數據類型的實用概覽，以及如何高效使用它們，還包含了許多使用示例和實踐提示。你現在並不需要閱讀它，但是要考慮將它作為寶貴的參考。

2.2 數據抽象

來源：2.2 Data Abstraction

譯者：飛龍

協議：CC BY-NC-SA 4.0

由於我們希望在程序中表達世界中的大量事物，我們發現它們的大多數都具有複合結構。日期是年月日，地理位置是精度和緯度。為了表示位置，我們希望程序語言具有將精度和緯度“粘合”為一對數據的能力 -- 也就是一個複合數據結構 -- 使我們的程序能夠以一種方式操作數據，將位置看做單個概念單元，它擁有兩個部分。

複合數據的使用也讓我們增加程序的模塊性。如果我們可以直接將地理位置看做對象來操作，我們就可以將程序的各個部分分離，它們根據這些值如何表示來從本質上處理這些值。將某個部分從程序中分離的一般技巧是一種叫做數據抽象的強大的設計方法論。這個部分用於處理數據表示，而程序用於操作數據。數據抽象使程序更易於設計、維護和修改。

數據抽象的特徵類似於函數抽象。當我們創建函數抽象時，函數如何實現的細節被隱藏了，而且特定的函數本身可以被任何具有相同行為的函數替換。換句話說，我們可以構造抽象來使函數的使用方式和函數的實現細節分離。與之相似，數據抽象是一種方法論，使我們將複合數據對象的使用細節與它的構造方式隔離。

數據抽象的基本概念是構造操作抽象數據的程序。也就是說，我們的程序應該以一種方式來使用數據，對數據做出儘可能少的假設。同時，需要定義具體的數據表示，獨立於使用數據的程序。我們系統中這兩部分的接口是一系列函數，叫做選擇器和構造器，它們基於具體表示實現了抽象數據。為了演示這個技巧，我們需要考慮如何設計一系列函數來操作有理數。

當你閱讀下一節時，要記住當今編寫的多數 Python 代碼使用了非常高級的抽象數據類型，它們內建於語言中，比如類、字典和列表。由於我們正在瞭解這些抽象的工作原理，我們自己不能使用它們。所以，我們會編寫一些不那麼 Python 化的代碼 -- 它並不是在語言中實現我們的概念的通常方式。但是，我們所編寫的代碼出於教育目的，它展示了這些抽象如何構建。要記住計算機科學並不只是學習如何使用編程語言，也學習它們的工作原理。

2.2.1 示例：有理數的算術

有理數可表示為整數的比值，並且它組成了實數的一個重要子類。類似於1/3或者17/29的有理數通常可編寫為：

<numerator>/<denominator>

其中，<numerator>和<denominator>都是值為整數的佔位符。有理數的值需要兩部分來描述。

有理數在計算機科學中很重要，因為它們就像整數那樣，可以準確表示。無理數（比如pi 或者 e 或者 sqrt(2)）會使用有限的二元展開代替為近似值。所以在原則上，有理數的處理應該讓我們避免算術中的近似誤差。

但是，一旦我們真正將分子與分母相除，我們就會只剩下截斷的小數近似值：

>>> 1/3
0.3333333333333333

當我們開始執行測試時，這個近似值的問題就會出現：

>>> 1/3 == 0.333333333333333300000  # Beware of approximations
True

計算機如何將實數近似為定長的小數擴展，是另一門課的話題。這裡的重要概念是，通過將有理數表示為整數的比值，我們能夠完全避免近似問題。所以出於精確，我們希望將分子和分母分離，但是將它們看做一個單元。

我們從函數抽象中瞭解到，我們可以在瞭解某些部分的實現之前開始編出東西來。讓我們一開始假設我們已經擁有一種從分子和分母中構造有理數的方式。我們也假設，給定一個有理數，我們都有辦法來提取（或選中）它的分子和分母。讓我們進一步假設，構造器和選擇器以下面三個函數來提供：

• make_rat(n, d)返回分子為n和分母為d的有理數。
• numer(x)返回有理數x的分子。
• denom(x)返回有理數x的分母。

我們在這裡正在使用一個強大的合成策略：心想事成。我們並沒有說有理數如何表示，或者numer、denom和make_rat如何實現。即使這樣，如果我們擁有了這三個函數，我們就可以執行加法、乘法，以及測試有理數的相等性，通過調用它們：

>>> def add_rat(x, y):
        nx, dx = numer(x), denom(x)
        ny, dy = numer(y), denom(y)
        return make_rat(nx * dy + ny * dx, dx * dy)
>>> def mul_rat(x, y):
        return make_rat(numer(x) * numer(y), denom(x) * denom(y))
>>> def eq_rat(x, y):
        return numer(x) * denom(y) == numer(y) * denom(x)

現在我們擁有了由選擇器函數numer和denom，以及構造器函數make_rat定義的有理數操作。但是我們還沒有定義這些函數。我們需要以某種方式來將分子和分母粘合為一個單元。

2.2.2 元組

為了實現我們的數據抽象的具體層面，Python 提供了一種複合數據結構叫做tuple，它可以由逗號分隔的值來構造。雖然並不是嚴格要求，圓括號通常在元組周圍。

>>> (1, 2)
(1, 2)

元組的元素可以由兩種方式解構。第一種是我們熟悉的多重賦值：

>>> pair = (1, 2)
>>> pair
(1, 2)
>>> x, y = pair
>>> x
1
>>> y
2

實際上，多重賦值的本質是創建和解構元組。

訪問元組元素的第二種方式是通過下標運算符，寫作方括號：

>>> pair[0]
1
>>> pair[1]
2

Python 中的元組（以及多數其它編程語言中的序列）下標都以 0 開始，也就是說，下標 0 表示第一個元素，下標 1 表示第二個元素，以此類推。我們對這個下標慣例的直覺是，下標表示一個元素距離元組開頭有多遠。

與元素選擇操作等價的函數叫做__getitem__，它也使用位置在元組中選擇元素，位置的下標以 0 開始。

>>> from operator import getitem
>>> getitem(pair, 0)
1

元素是原始類型，也就是說 Python 的內建運算符可以操作它們。我們不久之後再來看元素的完整特性。現在，我們只對元組如何作為膠水來實現抽象數據類型感興趣。

**表示有理數。**元素提供了一個自然的方式來將有理數實現為一對整數：分子和分母。我們可以通過操作二元組來實現我們的有理數構造器和選擇器函數。

>>> def make_rat(n, d):
        return (n, d)
>>> def numer(x):
        return getitem(x, 0)
>>> def denom(x):
        return getitem(x, 1)

用於打印有理數的函數完成了我們對抽象數據結構的實現。

>>> def str_rat(x):
        """Return a string 'n/d' for numerator n and denominator d."""
        return '{0}/{1}'.format(numer(x), denom(x))

將它與我們之前定義的算術運算放在一起，我們可以使用我們定義的函數來操作有理數了。

>>> half = make_rat(1, 2)
>>> str_rat(half)
'1/2'
>>> third = make_rat(1, 3)
>>> str_rat(mul_rat(half, third))
'1/6'
>>> str_rat(add_rat(third, third))
'6/9'

就像最後的例子所展示的那樣，我們的有理數實現並沒有將有理數化為最簡。我們可以通過修改make_rat來補救。如果我們擁有用於計算兩個整數的最大公約數的函數，我們可以在構造一對整數之前將分子和分母化為最簡。這可以使用許多實用工具，例如 Python 庫中的現存函數。

>>> from fractions import gcd
>>> def make_rat(n, d):
        g = gcd(n, d)
        return (n//g, d//g)

雙斜槓運算符//表示整數除法，它會向下取整除法結果的小數部分。由於我們知道g能整除n和d，整數除法正好適用於這裡。現在我們的

>>> str_rat(add_rat(third, third))
'2/3'

符合要求。這個修改只通過修改構造器來完成，並沒有修改任何實現實際算術運算的函數。

**擴展閱讀。**上面的str_rat實現使用了格式化字符串，它包含了值的佔位符。如何使用格式化字符串和format方法的細節請見 Dive Into Python 3 的格式化字符串一節。

2.2.3 抽象界限

在以更多複合數據和數據抽象的例子繼續之前，讓我們思考一些由有理數示例產生的問題。我們使用構造器make_rat和選擇器numer和denom定義了操作。通常，數據抽象的底層概念是，基於某個值的類型的操作如何表達，為這個值的類型確定一組基本的操作。之後使用這些操作來操作數據。

我們可以將有理數系統想象為一系列層級。

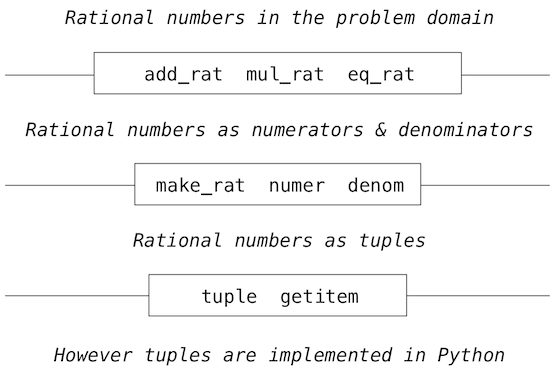
平行線表示隔離系統不同層級的界限。每一層上，界限分離了使用數據抽象的函數（上面）和實現數據抽象的函數（下面）。使用有理數的程序僅僅通過算術函數來操作它們：add_rat、mul_rat和eq_rat。相應地，這些函數僅僅由構造器和選擇器make_rat、numer和and denom來實現，它們本身由元組實現。元組如何實現的字節和其它層級沒有關係，只要元組支持選擇器和構造器的實現。

每一層上，盒子中的函數強制劃分了抽象的邊界，因為它們僅僅依賴於上層的表現（通過使用）和底層的實現（通過定義）。這樣，抽象界限可以表現為一系列函數。

抽象界限具有許多好處。一個好處就是，它們使程序更易於維護和修改。很少的函數依賴於特定的表現，當一個人希望修改表現時，不需要做很多修改。

2.2.4 數據屬性

我們通過實現算術運算來開始實現有理數，實現為這三個非特定函數：make_rat、numer和denom。這裡，我們可以認為已經定義了數據對象 -- 分子、分母和有理數 -- 上的運算，它們的行為由這三個函數規定。

但是數據意味著什麼？我們還不能說“提供的選擇器和構造器實現了任何東西”。我們需要保證這些函數一起規定了正確的行為。也就是說，如果我們從整數n和d中構造了有理數x，那麼numer(x)/denom(x)應該等於n/d。

通常，我們可以將抽象數據類型當做一些選擇器和構造器的集合，並帶有一些行為條件。只要滿足了行為條件（比如上面的除法特性），這些函數就組成了數據類型的有效表示。

這個觀點可以用在其他數據類型上，例如我們為實現有理數而使用的二元組。我們實際上不會談論元組是什麼，而是談論由語言提供的，用於操作和創建元組的運算符。我們現在可以描述二元組的行為條件，二元組通常叫做偶對，在表示有理數的問題中有所涉及。

為了實現有理數，我們需要一種兩個整數的粘合形式，它具有下列行為：

• 如果一個偶對p由x和y構造，那麼getitem_pair(p, 0)返回x，getitem_pair(p, 1)返回y。

我們可以實現make_pair和getitem_pair，它們和元組一樣滿足這個描述：

>>> def make_pair(x, y):
        """Return a function that behaves like a pair."""
        def dispatch(m):
            if m == 0:
                return x
            elif m == 1:
                return y
        return dispatch
>>> def getitem_pair(p, i):
        """Return the element at index i of pair p."""
        return p(i)

使用這個實現，我們可以創建和操作偶對：

>>> p = make_pair(1, 2)
>>> getitem_pair(p, 0)
1
>>> getitem_pair(p, 1)
2

這個函數的用法不同於任何直觀上的，數據應該是什麼的概念。而且，這些函數滿足於在我們的程序中表示覆合數據。

需要注意的微妙的一點是，由make_pair返回的值是叫做dispatch的函數，它接受參數m並返回x或y。之後，getitem_pair調用了這個函數來獲取合適的值。我們在這一章中會多次返回這個調度函數的話題。

這個偶對的函數表示並不是 Python 實際的工作機制（元組實現得更直接，出於性能因素），但是它可以以這種方式工作。這個函數表示雖然不是很明顯，但是是一種足夠完美來表示偶對的方式，因為它滿足了偶對唯一需要滿足的條件。這個例子也表明，將函數當做值來操作的能力，提供給我們表示複合數據的能力。

2.3 序列

來源：2.3 Sequences

譯者：飛龍

協議：CC BY-NC-SA 4.0

序列是數據值的順序容器。不像偶對只有兩個元素，序列可以擁有任意（但是有限）個有序元素。

序列在計算機科學中是強大而基本的抽象。例如，如果我們使用序列，我們就可以列出伯克利的每個學生，或者世界上的每所大學，或者每所大學中的每個學生。我們可以列出上過的每一門課，提交的每個作業，或者得到的每個成績。序列抽象讓數千個數據驅動的程序影響著我們每天的生活。

序列不是特定的抽象數據類型，而是不同類型共有的一組行為。也就是說，它們是許多序列種類，但是都有一定的屬性。特別地，

**長度。**序列擁有有限的長度。

**元素選擇。**序列的每個元素都擁有相應的非負整數作為下標，它小於序列長度，以第一個元素的 0 開始。

不像抽象數據類型，我們並沒有闡述如何構造序列。序列抽象是一組行為，它們並沒有完全指定類型（例如，使用構造器和選擇器），但是可以在多種類型中共享。序列提供了一個抽象層級，將特定程序如何操作序列類型的細節隱藏。

這一節中，我們開發了一個特定的抽象數據類型，它可以實現序列抽象。我們之後介紹實現相同抽象的 Python 內建類型。

2.3.1 嵌套偶對

對於有理數，我們使用二元組將兩個整數對象配對，之後展示了我們可以同樣通過函數來實現偶對。這種情況下，每個我們構造的偶對的元素都是整數。然而，就像表達式，元組可以嵌套。每個偶對的元素本身也可以是偶對，這個特性在實現偶對的任意一個方法，元組或調度函數中都有效。

可視化偶對的一個標準方法 -- 這裡也就是偶對(1,2) -- 叫做盒子和指針記號。每個值，複合或原始，都描述為指向盒子的指針。原始值的盒子只包含那個值的表示。例如，數值的盒子只包含數字。偶對的盒子實際上是兩個盒子：左邊的部分（箭頭指向的）包含偶對的第一個元素，右邊的部分包含第二個。

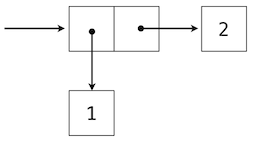
嵌套元素的 Python 表達式：

>>> ((1, 2), (3, 4))
((1, 2), (3, 4))

具有下面的結構：

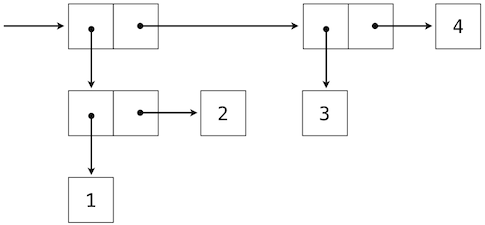
使用元組作為其它元組元素的能力，提供了我們編程語言中的一個新的組合手段。我們將這種將元組以這種方式嵌套的能力叫做元組數據類型的封閉性。通常，如果組合結果自己可以使用相同的方式組合，組合數據值的方式就滿足封閉性。封閉性在任何組合手段中都是核心能力，因為它允許我們創建層次數據結構 -- 結構由多個部分組成，它們自己也由多個部分組成，以此類推。我們在第三章會探索一些層次結構。現在，我們考慮一個特定的重要結構。

2.3.2 遞歸列表

我們可以使用嵌套偶對來構建任意長度的元素列表，它讓我們能夠實現抽象序列。下面的圖展示了四元素列表1, 2, 3, 4的遞歸表示：

這個列表由一系列偶對錶示。每個偶對的第一個元素是列表中的元素，而第二個元素是用於表示列表其餘部分的偶對。最後一個偶對的第二個元素是None，它表明列表到末尾了。我們可以使用嵌套的元組字面值來構造這個結構：

>>> (1, (2, (3, (4, None))))
(1, (2, (3, (4, None))))

這個嵌套的結構通常對應了一種非常實用的序列思考方式，我們在 Python 解釋器的執行規則中已經見過它了。一個非空序列可以劃分為：

• 它的第一個元素，以及
• 序列的其餘部分。

序列的其餘部分本身就是一個（可能為空的）序列。我們將序列的這種看法叫做遞歸，因為序列包含其它序列作為第二個組成部分。

由於我們的列表表示是遞歸的，我們在實現中叫它rlist，以便不會和 Python 內建的list類型混淆，我們會稍後在這一章介紹它。一個遞歸列表可以由第一個元素和列表的剩餘部分構造。None值表示空的遞歸列表。

>>> empty_rlist = None
>>> def make_rlist(first, rest):
        """Make a recursive list from its first element and the rest."""
        return (first, rest)
>>> def first(s):
        """Return the first element of a recursive list s."""
        return s[0]
>>> def rest(s):
        """Return the rest of the elements of a recursive list s."""
        return s[1]

這兩個選擇器和一個構造器，以及一個常量共同實現了抽象數據類型的遞歸列表。遞歸列表唯一的行為條件是，就像偶對那樣，它的構造器和選擇器是相反的函數。

• 如果一個遞歸列表s由元素f和列表r構造，那麼first(s)返回f，並且rest(s)返回r。

我們可以使用構造器和選擇器來操作遞歸列表。

>>> counts = make_rlist(1, make_rlist(2, make_rlist(3, make_rlist(4, empty_rlist))))
>>> first(counts)
1
>>> rest(counts)
(2, (3, (4, None)))

遞歸列表可以按序儲存元素序列，但是它還沒有實現序列的抽象。使用我們已經定義的數據類型抽象，我們就可以實現描述兩個序列的行為：長度和元素選擇。

>>> def len_rlist(s):
        """Return the length of recursive list s."""
        length = 0
        while s != empty_rlist:
            s, length = rest(s), length + 1
        return length
>>> def getitem_rlist(s, i):
        """Return the element at index i of recursive list s."""
        while i > 0:
            s, i = rest(s), i - 1
        return first(s)

現在，我們可以將遞歸列表用作序列了：

>>> len_rlist(counts)
4
>>> getitem_rlist(counts, 1)  # The second item has index 1
2

兩個實現都是可迭代的。它們隔離了嵌套偶對的每個層級，直到列表的末尾（在len_rlist中），或者到達了想要的元素（在getitem_rlist中）。

下面的一系列環境圖示展示了迭代過程，getitem_rlist通過它找到了遞歸列表中下標1中的元素2。

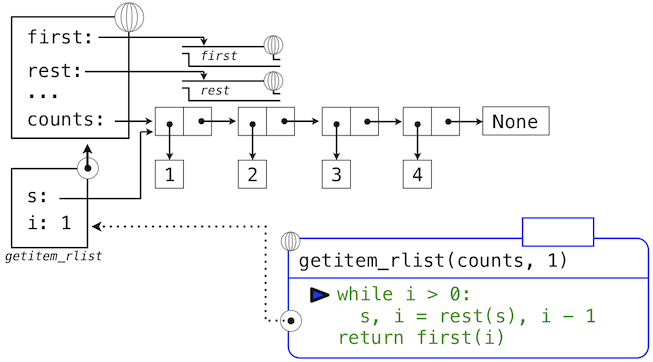
while頭部中的表達式求值為真，這會導致while語句組中的賦值語句被執行：

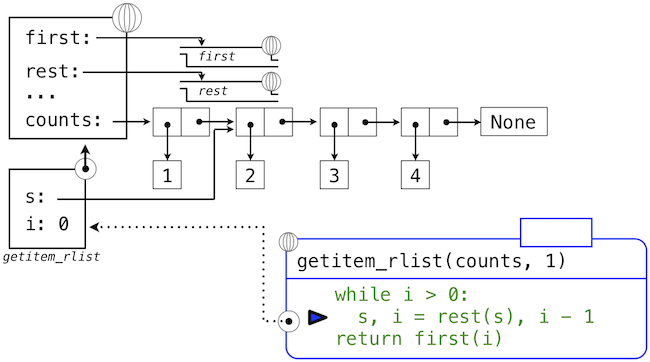
這裡，局部名稱s現在指向以原列表第二個元素開始的子列表。現在，while頭中的表達式求值為假，於是 Python 會求出getitem_rlist最後一行中返回語句中的表達式。

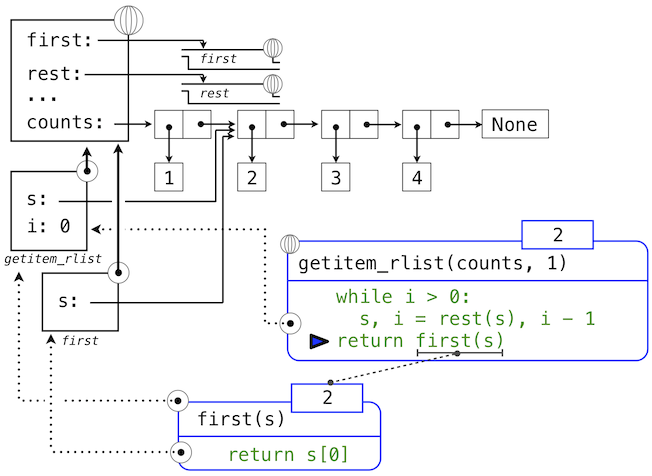
最後的環境圖示展示了調用first的局部幀，它包含綁定到相同子列表的s。first函數挑選出值2並返回了它，完成了getitem_rlist的調用。

這個例子演示了遞歸列表計算的常見模式，其中迭代的每一步都操作原列表的一個逐漸變短的後綴。尋找遞歸列表的長度和元素的漸進式處理過程需要一些時間來計算。（第三章中，我們會學會描述這種函數的計算時間。）Python 的內建序列類型以不同方式實現，它對於計算序列長度和獲取元素並不具有大量的計算開銷。

2.3.2 元組 II

實際上，我們引入用於形成原始偶對的tuple類型本身就是完整的序列類型。元組比起我們以函數式實現的偶對抽象數據結構，本質上提供了更多功能。

元組具有任意的長度，並且也擁有序列抽象的兩個基本行為：長度和元素選擇。下面的digits是一個四元素元組。

>>> digits = (1, 8, 2, 8)
>>> len(digits)
4
>>> digits[3]
8

此外，元素可以彼此相加以及與整數相乘。對於元組，加法和乘法操作並不對元素相加或相乘，而是組合和重複元組本身。也就是說，operator模塊中的add函數（以及+運算符）返回兩個被加參數連接成的新元組。operator模塊中的mul函數（以及*運算符）接受整數k和元組，並返回含有元組參數k個副本的新元組。

>>> (2, 7) + digits * 2
(2, 7, 1, 8, 2, 8, 1, 8, 2, 8)

**映射。**將一個元組變換為另一個元組的強大手段是在每個元素上調用函數，並收集結果。這一計算的常用形式叫做在序列上映射函數，對應內建函數map。map的結果是一個本身不是序列的對象，但是可以通過調用tuple來轉換為序列。它是元組的構造器。

>>> alternates = (-1, 2, -3, 4, -5)
>>> tuple(map(abs, alternates))
(1, 2, 3, 4, 5)

map函數非常重要，因為它依賴於序列抽象：我們不需要關心底層元組的結構，只需要能夠獨立訪問每個元素，以便將它作為參數傳入用於映射的函數中（這裡是abs）。

2.3.4 序列迭代

映射本身就是通用計算模式的一個實例：在序列中迭代所有元素。為了在序列上映射函數，我們不僅僅需要選擇特定的元素，還要依次選擇每個元素。這個模式非常普遍，Python 擁有額外的控制語句來處理序列數據：for語句。

考慮一個問題，計算一個值在序列中出現了多少次。我們可以使用while循環實現一個函數來計算這個數量。

>>> def count(s, value):
        """Count the number of occurrences of value in sequence s."""
        total, index = 0, 0
        while index < len(s):
            if s[index] == value:
                total = total + 1
            index = index + 1
        return total
>>> count(digits, 8)
2

Python for語句可以通過直接迭代元素值來簡化這個函數體，完全不需要引入index。例如（原文是For example，為雙關語），我們可以寫成：

>>> def count(s, value):
        """Count the number of occurrences of value in sequence s."""
        total = 0
        for elem in s:
            if elem == value:
                total = total + 1
        return total
>>> count(digits, 8)
2

for語句按照以下過程來執行：

1. 求出頭部表達式<expression>，它必須產生一個可迭代的值。
2. 對於序列中的每個元素值，按順序：
   1. 在局部環境中將變量名<name>綁定到這個值上。
   2. 執行語句組<suite>。

步驟 1 引用了可迭代的值。序列是可迭代的，它們的元素可看做迭代的順序。Python 的確擁有其他可迭代類型，但是我們現在只關注序列。術語“可迭代對象”的一般定義會在第四章的迭代器一節中出現。

這個求值過程的一個重要結果是，在for語句執行完畢之後，<name>會綁定到序列的最後一個元素上。這個for循環引入了另一種方式，其中局部環境可以由語句來更新。

**序列解構。**程序中的一個常見模式是，序列的元素本身就是序列，但是具有固定的長度。for語句可在頭部中包含多個名稱，將每個元素序列“解構”為各個元素。例如，我們擁有一個偶對（也就是二元組）的序列：

>>> pairs = ((1, 2), (2, 2), (2, 3), (4, 4))

下面的for語句的頭部帶有兩個名詞，會將每個名稱x和y分別綁定到每個偶對的第一個和第二個元素上。

>>> for x, y in pairs:
        if x == y:
            same_count = same_count + 1
>>> same_count
2

這個綁定多個名稱到定長序列中多個值的模式，叫做序列解構。它的模式和我們在賦值語句中看到的，將多個名稱綁定到多個值的模式相同。

範圍。range是另一種 Python 的內建序列類型，它表示一個整數範圍。範圍可以使用range函數來創建，它接受兩個整數參數：所得範圍的第一個數值和最後一個數值加一。

>>> range(1, 10)  # Includes 1, but not 10
range(1, 10)

在範圍上調用tuple構造器會創建與範圍具有相同元素的元組，使元素易於查看。

>>> tuple(range(5, 8))
(5, 6, 7)

如果只提供了一個元素，它會解釋為最後一個數值加一，範圍開始於 0。

>>> total = 0
>>> for k in range(5, 8):
        total = total + k
>>> total
18

常見的慣例是將單下劃線字符用於for頭部，如果這個名稱在語句組中不會使用。

>>> for _ in range(3):
        print('Go Bears!')

Go Bears!
Go Bears!
Go Bears!

要注意對解釋器來說，下劃線只是另一個名稱，但是在程序員中具有固定含義，它表明這個名稱不應出現在任何表達式中。

2.3.5 序列抽象

我們已經介紹了兩種原生數據類型，它們實現了序列抽象：元組和範圍。兩個都滿足這一章開始時的條件：長度和元素選擇。Python 還包含了兩種序列類型的行為，它們擴展了序列抽象。

**成員性。**可以測試一個值在序列中的成員性。Python 擁有兩個操作符in和not in，取決於元素是否在序列中出現而求值為True和False。

>>> digits
(1, 8, 2, 8)
>>> 2 in digits
True
>>> 1828 not in digits
True

所有序列都有叫做index和count的方法，它會返回序列中某個值的下標（或者數量）。

**切片。**序列包含其中的子序列。我們在開發我們的嵌套偶對實現時觀察到了這一點，它將序列切分為它的第一個元素和其餘部分。序列的切片是原序列的任何部分，由一對整數指定。就像range構造器那樣，第一個整數表示切片的起始下標，第二個表示結束下標加一。

Python 中，序列切片的表示類似於元素選擇，使用方括號。冒號分割了起始和結束下標。任何邊界上的省略都被當作極限值：起始下標為 0，結束下標是序列長度。

>>> digits[0:2]
(1, 8)
>>> digits[1:]
(8, 2, 8)

Python 序列抽象的這些額外行為的枚舉，給我們了一個機會來反思數據抽象通常由什麼構成。抽象的豐富性（也就是說它包含行為的多少）非常重要。對於使用抽象的用戶，額外的行為很有幫助，另一方面，滿足新類型抽象的豐富需求是個挑戰。為了確保我們的遞歸列表實現支持這些額外的行為，需要一些工作量。另一個抽象豐富性的負面結果是，它們需要用戶長時間學習。

序列擁有豐富的抽象，因為它們在計算中無處不在，所以學習一些複雜的行為是合理的。通常，多數用戶定義的抽象應該儘可能簡單。

**擴展閱讀。**切片符號接受很多特殊情況，例如負的起始值，結束值和步長。Dive Into Python 3 中有一節叫做列表切片，完整描述了它。這一章中，我們只會用到上面描述的基本特性。

2.3.6 字符串

文本值可能比數值對計算機科學來說更基本。作為一個例子，Python 程序以文本編寫和儲存。Python 中原生的文本數據類型叫做字符串，相應的構造器是str。

關於字符串在 Python 中如何表示和操作有許多細節。字符串是豐富抽象的另一個示例，程序員需要滿足一些實質性要求來掌握。這一節是字符串基本行為的摘要。

字符串字面值可以表達任意文本，被單引號或者雙引號包圍。

>>> 'I am string!'
'I am string!'
>>> "I've got an apostrophe"
"I've got an apostrophe"
>>> '您好'
'您好'

我們已經在代碼中見過字符串了，在print的調用中作為文檔字符串，以及在assert語句中作為錯誤信息。

字符串滿足兩個基本的序列條件，我們在這一節開始介紹過它們：它們擁有長度並且支持元素選擇。

>>> city = 'Berkeley'
>>> len(city)
8
>>> city[3]
'k'

字符串的元素本身就是包含單一字符的字符串。字符是字母表中的任意單一字符，標點符號，或者其它符號。不像許多其它編程語言那樣，Python 沒有單獨的字符類型，任何文本都是字符串，表示單一字符的字符串長度為 1、

就像元組，字符串可以通過加法和乘法來組合：

>>> city = 'Berkeley'
>>> len(city)
8
>>> city[3]
'k'

字符串的行為不同於 Python 中其它序列類型。字符串抽象沒有實現我們為元組和範圍描述的完整序列抽象。特別地，字符串上實現了成員性運算符in，但是與序列上的實現具有完全不同的行為。它匹配子字符串而不是元素。

>>> 'here' in "Where's Waldo?"
True

與之相似，字符串上的count和index方法接受子串作為參數，而不是單一字符。count的行為有細微差別，它統計字符串中非重疊字串的出現次數。

>>> 'Mississippi'.count('i')
4
>>> 'Mississippi'.count('issi')
1

**多行文本。**字符串並不限制於單行文本，三個引號分隔的字符串字面值可以跨越多行。我們已經在文檔字符串中使用了三個引號。

>>> """The Zen of Python
claims, Readability counts.
Read more: import this."""
'The Zen of Python\nclaims, "Readability counts."\nRead more: import this.'

在上面的打印結果中，\n（叫做“反斜槓加 n”）是表示新行的單一元素。雖然它表示為兩個字符（反斜槓和 n）。它在長度和元素選擇上被認為是單個字符。

**字符串強制。**字符串可以從 Python 的任何對象通過以某個對象值作為參數調用str構造函數來創建，這個字符串的特性對於從多種類型的對象中構造描述性字符串非常實用。

>>> str(2) + ' is an element of ' + str(digits)
'2 is an element of (1, 8, 2, 8)'

str函數可以以任何類型的參數調用，並返回合適的值，這個機制是後面的泛用函數的主題。

**方法。**字符串在 Python 中的行為非常具有生產力，因為大量的方法都返回字符串的變體或者搜索其內容。一部分這些方法由下面的示例介紹。

>>> '1234'.isnumeric()
True
>>> 'rOBERT dE nIRO'.swapcase()
'Robert De Niro'
>>> 'snakeyes'.upper().endswith('YES')
True

**擴展閱讀。**計算機中的文本編碼是個複雜的話題。這一章中，我們會移走字符串如何表示的細節，但是，對許多應用來說，字符串如何由計算機編碼的特定細節是必要的知識。Dive Into Python 3 的 4.1 ~ 4.3 節提供了字符編碼和 Unicode 的描述。

2.3.7 接口約定

在複合數據的處理中，我們強調了數據抽象如何讓我們設計程序而不陷入數據表示的細節，以及抽象如何為我們保留靈活性來嘗試備用表示。這一節中，我們引入了另一種強大的設計原則來處理數據結構 -- 接口約定的用法。

接口約定使在許多組件模塊中共享的數據格式，它可以混合和匹配來展示數據。例如，如果我們擁有多個函數，它們全部接受序列作為參數並且返回序列值，我們就可以把它們每一個用於上一個的輸出上，並選擇任意一種順序。這樣，我們就可以通過將函數鏈接成流水線，來創建一個複雜的過程，每個函數都是簡單而專一的。

這一節有兩個目的，來介紹以接口約定組織程序的概念，以及展示模塊化序列處理的示例。

考慮下面兩個問題，它們首次出現，並且只和序列的使用相關。

1. 對前n個斐波那契數中的偶數求和。
2. 列出一個名稱中的所有縮寫字母，它包含每個大寫單詞的首字母。

這些問題是有關係的，因為它們可以解構為簡單的操作，它們接受序列作為輸入，併產出序列作為輸出。而且，這些操作是序列上的計算的一般方法的實例。讓我們思考第一個問題，它可以解構為下面的步驟：

 enumerate     map    filter  accumulate
-----------    ---    ------  ----------
naturals(n)    fib    iseven     sum

下面的fib函數計算了斐波那契數（現在使用了for語句更新了第一章中的定義）。

>>> def fib(k):
        """Compute the kth Fibonacci number."""
        prev, curr = 1, 0  # curr is the first Fibonacci number.
        for _ in range(k - 1):
             prev, curr = curr, prev + curr
        return curr

謂詞iseven可以使用整數取餘運算符%來定義。

>>> def iseven(n):
        return n % 2 == 0

map和filter函數是序列操作，我們已經見過了map，它在序列中的每個元素上調用函數並且收集結果。filter函數接受序列，並且返回序列中謂詞為真的元素。兩個函數都返回間接對象，map和filter對象，它們是可以轉換為元組或求和的可迭代對象。

>>> nums = (5, 6, -7, -8, 9)
>>> tuple(filter(iseven, nums))
(6, -8)
>>> sum(map(abs, nums))
35

現在我們可以實現even_fib，第一個問題的解，使用map、filter和sum。

>>> def sum_even_fibs(n):
        """Sum the first n even Fibonacci numbers."""
        return sum(filter(iseven, map(fib, range(1, n+1))))
>>> sum_even_fibs(20)
3382

現在，讓我們思考第二個問題。它可以解構為序列操作的流水線，包含map和filter。

enumerate  filter   map   accumulate
---------  ------  -----  ----------
  words    iscap   first    tuple

字符串中的單詞可以通過字符串對象上的split方法來枚舉，默認以空格分割。

>>> tuple('Spaces between words'.split())
('Spaces', 'between', 'words')

單詞的第一個字母可以使用選擇運算符來獲取，確定一個單詞是否大寫的謂詞可以使用內建謂詞isupper定義。

>>> def first(s):
        return s[0]
>>> def iscap(s):
        return len(s) > 0 and s[0].isupper()

這裡，我們的縮寫函數可以使用map和filter定義。

>>> def acronym(name):
        """Return a tuple of the letters that form the acronym for name."""
        return tuple(map(first, filter(iscap, name.split())))
>>> acronym('University of California Berkeley Undergraduate Graphics Group')
('U', 'C', 'B', 'U', 'G', 'G')

這些不同問題的相似解法展示瞭如何使用通用的計算模式，例如映射、過濾和累計，來組合序列的接口約定上的操作。序列抽象讓我們編寫出這些簡明的解法。

將程序表達為序列操作有助於我們設計模塊化的程序。也就是說，我們的設計由組合相關的獨立片段構建，每個片段都對序列進行轉換。通常，我們可以通過提供帶有接口約定的標準組件庫來鼓勵模塊化設計，接口約定以靈活的方式連接這些組件。

**生成器表達式。**Python 語言包含第二個處理序列的途徑，叫做生成器表達式。它提供了與map和reduce相似的功能，但是需要更少的函數定義。

生成器表達式組合了過濾和映射的概念，並集成於單一的表達式中，以下面的形式：

<map expression> for <name> in <sequence expression> if <filter expression>

為了求出生成器表達式，Python 先求出<sequence expression>，它必須返回一個可迭代值。之後，對於每個元素，按順序將元素值綁定到<name>，求出過濾器表達式，如果它產生真值，就會求出映射表達式。

生成器表達式的求解結果值本身是個可迭代值。累計函數，比如tuple、sum、max和min可以將返回的對象作為參數。

>>> def acronym(name):
        return tuple(w[0] for w in name.split() if iscap(w))
>>> def sum_even_fibs(n):
        return sum(fib(k) for k in range(1, n+1) if fib(k) % 2 == 0)

生成器表達式是使用可迭代（例如序列）接口約定的特化語法。這些表達式包含了map和filter的大部分功能，但是避免了被調用函數的實際創建（或者，順便也避免了環境幀的創建需要調用這些函數）。

**歸約。**在我們的示例中，我們使用特定的函數來累計結果，例如tuple或者sum。函數式編程語言（包括 Python）包含通用的高階累加器，具有多種名稱。Python 在functools模塊中包含reduce，它對序列中的元素從左到右依次調用二元函數，將序列歸約為一個值。下面的表達式計算了五個因數的積。

>>> from operator import mul
>>> from functools import reduce
>>> reduce(mul, (1, 2, 3, 4, 5))
120

使用這個更普遍的累計形式，除了求和之外，我們也可以計算斐波那契數列中奇數的積，將序列用作接口約定。

>>> def product_even_fibs(n):
        """Return the product of the first n even Fibonacci numbers, except 0."""
        return reduce(mul, filter(iseven, map(fib, range(2, n+1))))
>>> product_even_fibs(20)
123476336640

與map、filter和reduce對應的高階過程的組合會再一次在第四章出現，在我們思考多臺計算機之間的分佈式計算方法的時候。

2.4 可變數據

來源：2.4 Mutable Data

譯者：飛龍

協議：CC BY-NC-SA 4.0

我們已經看到了抽象在幫助我們應對大型系統的複雜性時如何至關重要。有效的程序整合也需要一些組織原則，指導我們構思程序的概要設計。特別地，我們需要一些策略來幫助我們構建大型系統，使之模塊化。也就是說，它們可以“自然”劃分為可以分離開發和維護的各個相關部分。

我們用於創建模塊化程序的強大工具之一，是引入可能會隨時間改變的新類型數據。這樣，單個數據可以表示獨立於其他程序演化的東西。對象行為的改變可能會由它的歷史影響，就像世界中的實體那樣。向數據添加狀態是這一章最終目標：面向對象編程的要素。

我們目前引入的原生數據類型 -- 數值、布爾值、元組、範圍和字符串 -- 都是不可變類型的對象。雖然名稱的綁定可以在執行過程中修改為環境中不同的值，但是這些值本身不會改變。這一章中，我們會介紹一組可變數據類型。可變對象可以在程序執行期間改變。

2.4.1 局部狀態

我們第一個可變對象的例子就是局部狀態。這個狀態會在程序執行期間改變。

為了展示函數的局部狀態是什麼東西，讓我們對從銀行取錢的情況進行建模。我們會通過創建叫做withdraw的函數來實現它，它將要取出的金額作為參數。如果賬戶中有足夠的錢來取出，withdraw應該返回取錢之後的餘額。否則，withdraw應該返回消息'Insufficient funds'。例如，如果我們以賬戶中的$100開始，我們希望通過調用withdraw來得到下面的序列：

>>> withdraw(25)
75
>>> withdraw(25)
50
>>> withdraw(60)
'Insufficient funds'
>>> withdraw(15)
35

觀察表達式withdraw(25)，求值了兩次，產生了不同的值。這是一種用戶定義函數的新行為：它是非純函數。調用函數不僅僅返回一個值，同時具有以一些方式修改函數的副作用，使帶有相同參數的下次調用返回不同的結果。我們所有用戶定義的函數，到目前為止都是純函數，除非他們調用了非純的內建函數。它們仍舊是純函數，因為它們並不允許修改任何在局部環境幀之外的東西。

為了使withdraw有意義，它必須由一個初始賬戶餘額創建。make_withdraw函數是個高階函數，接受起始餘額作為參數，withdraw函數是它的返回值。

>>> withdraw = make_withdraw(100)

make_withdraw的實現需要新類型的語句：nonlocal語句。當我們調用make_withdraw時，我們將名稱balance綁定到初始值上。之後我們定義並返回了局部函數，withdraw，它在調用時更新並返回balance的值。

>>> def make_withdraw(balance):
        """Return a withdraw function that draws down balance with each call."""
        def withdraw(amount):
            nonlocal balance                 # Declare the name "balance" nonlocal
            if amount > balance:
                return 'Insufficient funds'
            balance = balance - amount       # Re-bind the existing balance name
            return balance
        return withdraw

這個實現的新奇部分是nonlocal語句，無論什麼時候我們修改了名稱balance的綁定，綁定都會在balance所綁定的第一個幀中修改。回憶一下，在沒有nonlocal語句的情況下，賦值語句總是會在環境的第一個幀中綁定名稱。nonlocal語句表明，名稱出現在環境中不是第一個（局部）幀，或者最後一個（全局）幀的其它地方。

我們可以將這些修改使用環境圖示來可視化。下面的環境圖示展示了每個調用的效果，以上面的定義開始。我們省略了函數值中的代碼，以及不在我們討論中的表達式樹。

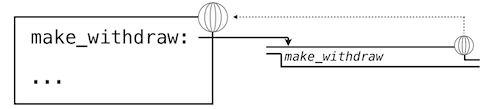
我們的定義語句擁有平常的效果：它創建了新的用戶定義函數，並且將名稱make_withdraw在全局幀中綁定到那個函數上。

下面，我們使用初始的餘額參數20來調用make_withdraw。

>>> wd = make_withdraw(20)

這個賦值語句將名稱wd綁定到全局幀中的返回函數上：

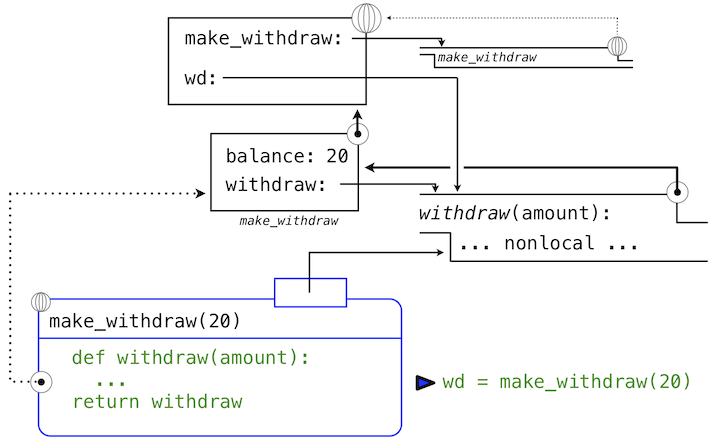
所返回的函數，（內部）叫做withdraw，和定義所在位置即make_withdraw的局部環境相關聯。名稱balance在這個局部環境中綁定。在例子的剩餘部分中，balance名稱只有這一個綁定，這非常重要。

下面，我們求出以總數5調用withdraw的表達式的值：

>>> wd(5)
15

名稱wd綁定到了withdraw函數上，所以withdraw的函數體在新的環境中求值，新的環境擴展自withdraw定義所在的環境。跟蹤withdraw求值的效果展示了 Python 中nonlocal語句的效果。

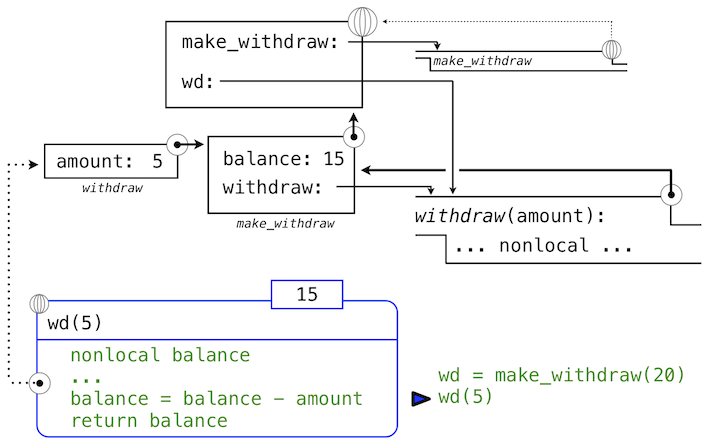
withdraw的賦值語句通常在withdraw的局部幀中為balance創建新的綁定。由於nonlocal語句，賦值運算找到了balance定義位置的第一幀，並在那裡重新綁定名稱。如果balance之前沒有綁定到值上，那麼nonlocal語句會產生錯誤。

通過修改balance綁定的行為，我們也修改了withdraw函數。下次withdraw調用的時候，名稱balance會求值為15而不是20。

當我們第二次調用wd時，

>>> wd(3)
12

我們發現綁定到balance的值的修改可在兩個調用之間積累。

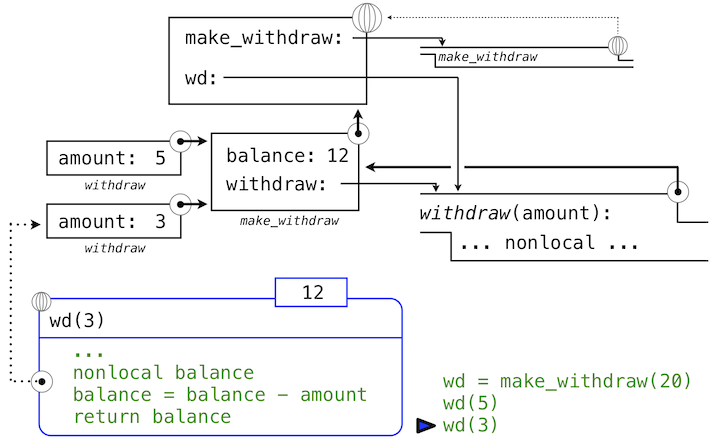
這裡，第二次調用withdraw會創建第二個局部幀，像之前一樣，但是，withdraw的兩個幀都擴展自make_withdraw的環境，它們都包含balance的綁定。所以，它們共享特定的名稱綁定，調用withdraw具有改變環境的副作用，並且會由之後的withdraw調用繼承。

**實踐指南。**通過引入nonlocal語句，我們發現了賦值語句的雙重作用。它們修改局部綁定，或者修改非局部綁定。實際上，賦值語句已經有了兩個作用：創建新的綁定，或者重新綁定現有名稱。Python 賦值的許多作用使賦值語句的執行效果變得模糊。作為一個程序員，你應該用文檔清晰記錄你的代碼，使賦值的效果可被其它人理解。

2.4.2 非局部賦值的好處

非局部賦值是將程序作為獨立和自主的對象觀察的重要步驟，對象彼此交互，但是各自管理各自的內部狀態。

特別地，非局部賦值提供了在函數的局部範圍中維護一些狀態的能力，這些狀態會在函數之後的調用中演化。和特定withdraw函數相關的balance在所有該函數的調用中共享。但是，withdraw實例中的balance綁定對程序的其餘部分不可見。只有withdraw關聯到了make_withdraw的幀，withdraw在那裡被定義。如果make_withdraw再次調用，它會創建單獨的幀，帶有單獨的balance綁定。

我們可以繼續以我們的例子來展示這個觀點。make_withdraw的第二個調用返回了第二個withdraw函數，它關聯到了另一個環境上。

>>> wd2 = make_withdraw(7)

第二個withdraw函數綁定到了全局幀的名稱wd2上。我們使用星號來省略了表示這個綁定的線。現在，我們看到實際上有兩個balance的綁定。名稱wd仍舊綁定到餘額為12的withdraw函數上，而wd2綁定到了餘額為7的新的withdraw函數上。

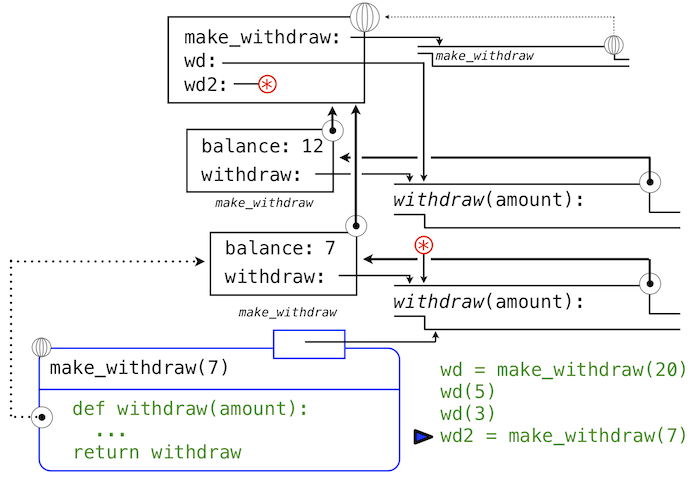
最後，我們調用綁定到wd2上的第二個withdraw函數：

>>> wd2(6)
1

這個調用修改了非局部名稱balance的綁定，但是不影響在全局幀中綁定到名稱wd的第一個withdraw。

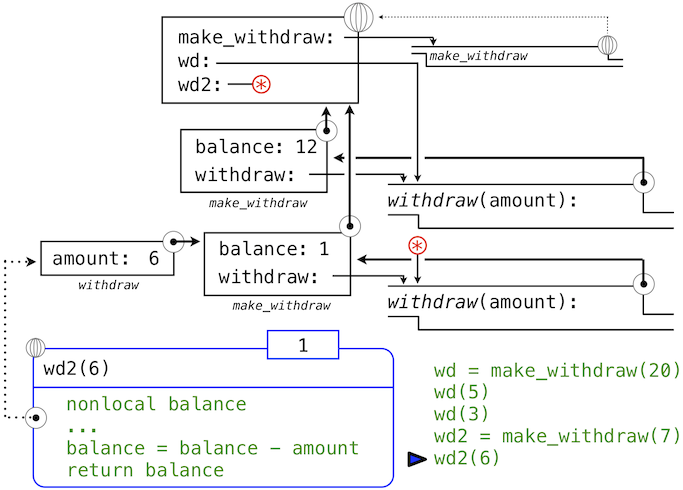
這樣，withdraw的每個實例都維護它自己的餘額狀態，但是這個狀態對程序中其它函數不可見。在更高層面上觀察這個情況，我們創建了銀行賬戶的抽象，它管理自己的內部狀態，但以一種方式對真實世界的賬戶進行建模：它基於自己的歷史提取請求來隨時間變化。

2.4.3 非局部賦值的代價

我們擴展了我們的計算環境模型，用於解釋非局部賦值的效果。但是，非局部複製與我們思考名稱和值的方式有一些細微差異。

之前，我們的值並沒有改變，僅僅是我們的名稱和綁定發生了變化。當兩個名稱a和b綁定到4上時，它們綁定到了相同的4還是不同的4並不重要。我們說，只有一個4對象，並且它永不會改變。

但是，帶有狀態的函數不是這樣的。當兩個名稱wd和wd2都綁定到withdraw函數時，它們綁定到相同函數還是函數的兩個不同實例，就很重要了。考慮下面的例子，它與我們之前分析的那個正好相反：

>>> wd = make_withdraw(12)
>>> wd2 = wd
>>> wd2(1)
11
>>> wd(1)
10

這裡，通過wd2調用函數會修改名稱為wd的函數的值，因為兩個名稱都指向相同的函數。這些語句執行之後的環境圖示展示了這個現象：

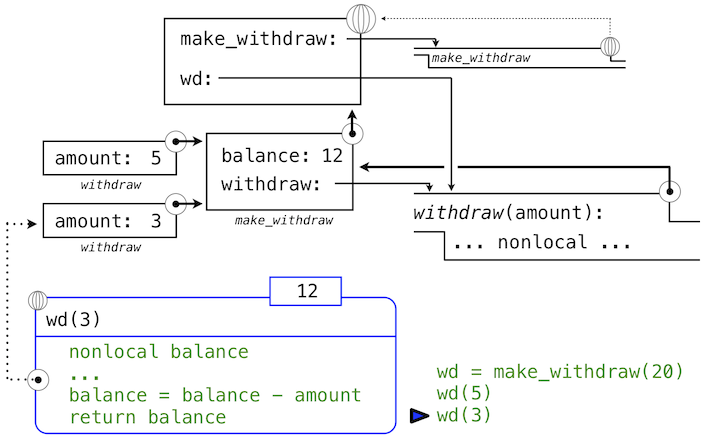
兩個名稱指向同一個值在世界上不常見，但我們程序中就是這樣。但是，由於值會隨時間改變，我們必須非常仔細來理解其它名稱上的變化效果，它們可能指向這些值。

正確分析帶有非局部賦值代碼的關鍵是，記住只有函數調用可以創建新的幀。賦值語句始終改變現有幀中的綁定。這裡，除非make_withdraw調用了兩次，balance還是隻有一個綁定。

**變與不變。**這些細微差別出現的原因是，通過引入修改非局部環境的非純函數，我們改變了表達式的本質。只含有純函數的表達式是引用透明（referentially transparent）的。如果我們將它的子表達式換成子表達式的值，它的值不會改變。

重新綁定的操作違反了引用透明的條件，因為它們不僅僅返回一個值。它們修改了環境。當我們引入任意重綁定的時候，我們就會遇到一個棘手的認識論問題：它對於兩個相同的值意味著什麼。在我們的計算環境模型中，兩個分別定義的函數並不是相同的，因為其中一個的改變並不影響另一個。

通常，只要我們不會修改數據對象，我們就可以將複合數據對象看做其部分的總和。例如，有理數可以通過提供分子和分母來確定。但是這個觀點在變化出現時不再成立了，其中複合數據對象擁有一個“身份”，不同於組成它的各個部分。即使我們通過取錢來修改了餘額，某個銀行賬戶還是“相同”的銀行賬戶。相反，我們可以讓兩個銀行賬戶碰巧具有相同的餘額，但它們是不同的對象。

儘管它引入了新的困難，非局部賦值是個創建模塊化編程的強大工具，程序的不同部分，對應不同的環境幀，可以在程序執行中獨立演化。而且，使用帶有局部狀態的函數，我們就能實現可變數據類型。在這一節的剩餘部分，我們介紹了一些最實用的 Python 內建數據類型，以及使用帶有非局部賦值的函數，來實現這些數據類型的一些方法。

2.4.4 列表

list是 Python 中最使用和靈活的數據類型。列表類似於元組，但是它是可變的。方法調用和賦值語句都可以修改列表的內容。

我們可以通過一個展示（極大簡化的）撲克牌歷史的例子，來介紹許多列表編輯操作。例子中的註釋描述了每個方法的效果。

撲克牌發明於中國，大概在 9 世紀。早期的牌組中有三個花色，它們對應錢的三個面額。

>>> chinese_suits = ['coin', 'string', 'myriad']  # A list literal
>>> suits = chinese_suits                         # Two names refer to the same list

撲克牌傳到歐洲（也可能通過埃及）之後，西班牙的牌組（oro）中之只保留了硬幣的花色。

>>> suits.pop()             # Removes and returns the final element
'myriad'
>>> suits.remove('string')  # Removes the first element that equals the argument

然後又添加了三個新的花色（它們的設計和名稱隨時間而演化），

>>> suits.append('cup')              # Add an element to the end
>>> suits.extend(['sword', 'club'])  # Add all elements of a list to the end

意大利人把劍叫做“黑桃”：

>>> suits[2] = 'spade'  # Replace an element

下面是傳統的意大利牌組：

>>> suits
['coin', 'cup', 'spade', 'club']

我們現在在美國使用的法式變體修改了前兩個：

>>> suits[0:2] = ['heart', 'diamond']  # Replace a slice
>>> suits
['heart', 'diamond', 'spade', 'club']

也存在用於插入、排序和反轉列表的操作。所有這些修改操作都改變了列表的值，它們並不創建新的列表對象。

**共享和身份。**由於我們修改了一個列表，而不是創建新的列表，綁定到名稱chinese_suits上的對象也改變了，因為它與綁定到suits上的對象是相同的列表對象。

>>> chinese_suits  # This name co-refers with "suits" to the same list
['heart', 'diamond', 'spade', 'club']

列表可以使用list構造函數來複制。其中一個的改變不會影響另一個，除非它們共享相同的結構。

>>> nest = list(suits)  # Bind "nest" to a second list with the same elements
>>> nest[0] = suits     # Create a nested list

在最後的賦值之後，我們只剩下下面的環境，其中列表使用盒子和指針的符號來表示：

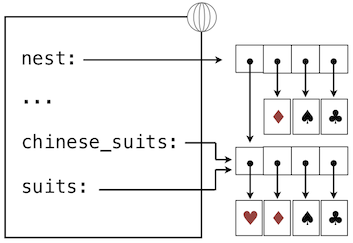
根據這個環境，修改由suites指向的列表會影響nest第一個元素的嵌套列表，但是不會影響其他元素：

>>> suits.insert(2, 'Joker')  # Insert an element at index 2, shifting the rest
>>> nest
[['heart', 'diamond', 'Joker', 'spade', 'club'], 'diamond', 'spade', 'club']

與之類似，在next的第一個元素上撤銷這個修改也會影響到suit。

由於這個pop方法的調用，我們返回到了上面描述的環境。

由於兩個列表具有相同內容，但是實際上是不同的列表，我們需要一種手段來測試兩個對象是否相同。Python 引入了兩個比較運算符，叫做is和is not，測試了兩個表達式實際上是否求值為同一個對象。如果兩個對象的當前值相等，並且一個對象的改變始終會影響另一個，那麼兩個對象是同一個對象。身份是個比相等性更強的條件。

譯者注：兩個對象當且僅當在內存中的位置相同時為同一個對象。CPython 的實現直接比較對象的地址來確定。

>>> suits is nest[0]
True
>>> suits is ['heart', 'diamond', 'spade', 'club']
False
>>> suits == ['heart', 'diamond', 'spade', 'club']
True

最後的兩個比較展示了is和==的區別，前者檢查身份，而後者檢查內容的相等性。

**列表推導式。**列表推導式使用擴展語法來創建列表，與生成器表達式的語法相似。

例如，unicodedata模塊跟蹤了 Unicode 字母表中每個字符的官方名稱。我們可以查找與名稱對應的字符，包含這些卡牌花色的字符。

>>> from unicodedata import lookup
>>> [lookup('WHITE ' + s.upper() + ' SUIT') for s in suits]
['♡', '♢', '♤', '♧']

列表推導式使用序列的接口約定增強了數據處理的範式，因為列表是一種序列數據類型。

**擴展閱讀。**Dive Into Python 3 的推導式一章包含了一些示例，展示瞭如何使用 Python 瀏覽計算機的文件系統。這一章介紹了os模塊，它可以列出目錄的內容。這個材料並不是這門課的一部分，但是推薦給任何想要增加 Python 知識和技巧的人。

**實現。**列表是序列，就像元組一樣。Python 語言並不提供給我們列表實現的直接方法，只提供序列抽象，和我們在這一節介紹的可變方法。為了克服這一語言層面的抽象界限，我們可以開發列表的函數式實現，再次使用遞歸表示。這一節也有第二個目的：加深我們對調度函數的理解。

我們會將列表實現為函數，它將一個遞歸列表作為自己的局部狀態。列表需要有一個身份，就像任何可變值那樣。特別地，我們不能使用None來表示任何空的可變列表，因為兩個空列表並不是相同的值（例如，向一個列表添加元素並不會添加到另一個），但是None is None。另一方面，兩個不同的函數足以區分兩個兩個空列表，它們都將empty_rlist作為局部狀態。

我們的可變列表是個調度函數，就像我們偶對的函數式實現也是個調度函數。它檢查輸入“信息”是否為已知信息，並且對每個不同的輸入執行相應的操作。我們的可變列表可響應五個不同的信息。前兩個實現了序列抽象的行為。接下來的兩個添加或刪除列表的第一個元素。最後的信息返回整個列表內容的字符串表示。

>>> def make_mutable_rlist():
        """Return a functional implementation of a mutable recursive list."""
        contents = empty_rlist
        def dispatch(message, value=None):
            nonlocal contents
            if message == 'len':
                return len_rlist(contents)
            elif message == 'getitem':
                return getitem_rlist(contents, value)
            elif message == 'push_first':
                contents = make_rlist(value, contents)
            elif message == 'pop_first':
                f = first(contents)
                contents = rest(contents)
                return f
            elif message == 'str':
                return str(contents)
        return dispatch

我們也可以添加一個輔助函數，來從任何內建序列中構建函數式實現的遞歸列表。只需要以遞歸順序添加每個元素。

>>> def to_mutable_rlist(source):
        """Return a functional list with the same contents as source."""
        s = make_mutable_rlist()
        for element in reversed(source):
            s('push_first', element)
        return s

在上面的定義中，函數reversed接受並返回可迭代值。它是使用序列的接口約定的另一個示例。

這裡，我們可以構造函數式實現的列表，要注意列表自身也是個函數。

>>> s = to_mutable_rlist(suits)
>>> type(s)
<class 'function'>
>>> s('str')
"('heart', ('diamond', ('spade', ('club', None))))"

另外，我們可以像列表s傳遞信息來修改它的內容，比如移除第一個元素。

>>> s('pop_first')
'heart'
>>> s('str')
"('diamond', ('spade', ('club', None)))"

原則上，操作push_first和pop_first足以對列表做任意修改。我們總是可以清空整個列表，之後將它舊的內容替換為想要的結果。

**消息傳遞。**給予一些時間，我們就能實現許多實用的 Python 列表可變操作，比如extend和insert。我們有一個選擇：我們可以將它們全部實現為函數，這會使用現有的消息pop_first和push_first來實現所有的改變操作。作為代替，我們也可以向dispatch函數體添加額外的elif子句，每個子句檢查一個消息（例如'extend'），並且直接在contents上做出合適的改變。

第二個途徑叫做消息傳遞，它把數據值上面所有操作的邏輯封裝在一個函數中，這個函數響應不同的消息。一個使用消息傳遞的程序定義了調度函數，每個函數都擁有局部狀態，通過傳遞“消息”作為第一個參數給這些函數來組織計算。消息是對應特定行為的字符串。

可以想象，在dispatch的函數體中通過名稱來枚舉所有這些消息非常無聊，並且易於出現錯誤。Python 的字典提供了一種數據類型，會幫助我們管理消息和操作之間的映射，它會在下一節中介紹。

2.4.5 字典

字典是 Python 內建數據類型，用於儲存和操作對應關係。字典包含了鍵值對，其中鍵和值都可以是對象。字典的目的是提供一種抽象，用於儲存和獲取下標不是連續整數，而是描述性的鍵的值。

字符串通常用作鍵，因為字符串通常用於表示事物名稱。這個字典字面值提供了不同羅馬數字的值。

>>> numerals = {'I': 1.0, 'V': 5, 'X': 10}

我們可以使用元素選擇運算符，來通過鍵查找值，我們之前將其用於序列。

>>> numerals['X']
10

字典的每個鍵最多隻能擁有一個值。添加新的鍵值對或者修改某個鍵的已有值，可以使用賦值運算符來完成。

>>> numerals['I'] = 1
>>> numerals['L'] = 50
>>> numerals
{'I': 1, 'X': 10, 'L': 50, 'V': 5}

要注意，'L'並沒有添加到上面輸出的末尾。字典是無序的鍵值對集合。當我們打印字典時，鍵和值都以某種順序來渲染，但是對語言的用戶來說，不應假設順序總是這樣。

字典抽象也支持多種方法，來從整體上迭代字典中的內容。方法keys、values和items都返回可迭代的值。

>>> sum(numerals.values())
66

通過調用dict構造函數，鍵值對的列表可以轉換為字典。

>>> dict([(3, 9), (4, 16), (5, 25)])
{3: 9, 4: 16, 5: 25}

字典也有一些限制：

• 字典的鍵不能是可變內建類型的對象。
• 一個給定的鍵最多隻能有一個值。

第一條限制被綁定到了 Python 中字典的底層實現上。這個實現的細節並不是這門課的主題。直覺上，鍵告訴了 Python 應該在內存中的哪裡尋找鍵值對；如果鍵發生改變，鍵值對就會丟失。

第二個限制是字典抽象的結果，它為儲存和獲取某個鍵的值而設計。如果字典中最多隻存在一個這樣的值，我們只能獲取到某個鍵的一個值。

由字典實現的一個實用方法是get，如果鍵存在的話，它返回鍵的值，否則返回一個默認值。get的參數是鍵和默認值。

>>> numerals.get('A', 0)
0
>>> numerals.get('V', 0)
5

字典也擁有推導式語法，和列表和生成器表達式類似。求解字典推導式會產生新的字典對象。

>>> {x: x*x for x in range(3,6)}
{3: 9, 4: 16, 5: 25}

**實現。**我們可以實現一個抽象數據類型，它是一個記錄的列表，與字典抽象一致。每個記錄都是兩個元素的列表，包含鍵和相關的值。

>>> def make_dict():
        """Return a functional implementation of a dictionary."""
        records = []
        def getitem(key):
            for k, v in records:
                if k == key:
                    return v
        def setitem(key, value):
            for item in records:
                if item[0] == key:
                    item[1] = value
                    return
            records.append([key, value])
        def dispatch(message, key=None, value=None):
            if message == 'getitem':
                return getitem(key)
            elif message == 'setitem':
                setitem(key, value)
            elif message == 'keys':
                return tuple(k for k, _ in records)
            elif message == 'values':
                return tuple(v for _, v in records)
        return dispatch

同樣，我們使用了傳遞方法的消息來組織我們的實現。我們已經支持了四種消息：getitem、setitem、keys和values。要查找某個鍵的值，我們可以迭代這些記錄來尋找一個匹配的鍵。要插入某個鍵的值，我們可以迭代整個記錄來觀察是否已經存在帶有這個鍵的記錄。如果沒有，我們會構造一條新的記錄。如果已經有了帶有這個鍵的記錄，我們將這個記錄的值設為新的值。

我們現在可以使用我們的實現來儲存和獲取值。

>>> d = make_dict()
>>> d('setitem', 3, 9)
>>> d('setitem', 4, 16)
>>> d('getitem', 3)
9
>>> d('getitem', 4)
16
>>> d('keys')
(3, 4)
>>> d('values')
(9, 16)

這個字典實現並不為快速的記錄檢索而優化，因為每個響應getitem消息都必須迭代整個records列表。內建的字典類型更加高效。

2.4.6 示例：傳播約束

可變數據允許我們模擬帶有變化的系統，也允許我們構建新的抽象類型。在這個延伸的實例中，我們組合了非局部賦值、列表和字典來構建一個基於約束的系統，支持多個方向上的計算。將程序表達為約束是一種聲明式編程，其中程序員聲明需要求解的問題結構，但是抽象了問題解決方案如何計算的細節。

計算機程序通常組織為單方向的計算，它在預先設定的參數上執行操作，來產生合理的輸出。另一方面，我們通常希望根據數量上的關係對系統建模。例如，我們之前考慮過理想氣體定律，它通過波爾茲曼常數k關聯了理想氣體的氣壓p，體積v，數量n以及溫度t。

p * v = n * k * t

這樣一個方程並不是單方向的。給定任何四個數量，我們可以使用這個方程來計算第五個。但將這個方程翻譯為某種傳統的計算機語言會強迫我們選擇一個數量，根據其餘四個計算出來。所以計算氣壓的函數應該不能用於計算溫度，即使二者的計算通過相同的方程完成。

這一節中，我們從零開始設計線性計算的通用模型。我們定義了數量之間的基本約束，例如adder(a, b, c)會嚴格保證數學關係a + b = c。

我們也定義了組合的手段，使基本約束可以被組合來表達更復雜的關係。這樣，我們的程序就像一種編程語言。我們通過構造網絡來組合約束，其中約束由連接器連接。連接器是一種對象，它“持有”一個值，並且可能會參與一個或多個約束。

例如，我們知道華氏和攝氏溫度的關係是：

9 * c = 5 * (f - 32)

這個等式是c和f之間的複雜約束。這種約束可以看做包含adder、multiplier和contant約束的網絡。

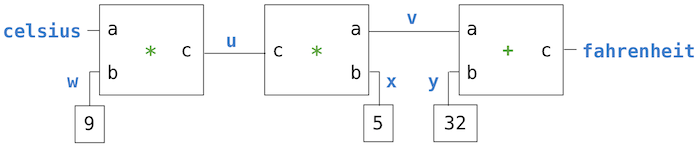
這張圖中，我們可以看到，左邊是一個帶有三個終端的乘法器盒子，標記為a，b和c。它們將乘法器連接到網絡剩餘的部分：終端a鏈接到了連接器celsius上，它持有攝氏溫度。終端b鏈接到了連接器w上，w也鏈接到持有9的盒子上。終端c，被乘法器盒子約束為a和b的乘積，鏈接到另一個乘法器盒子上，它的b鏈接到常數5上，以及它的a連接到了求和約束的一項上。

這個網絡上的計算會如下進行：當連接器被提供一個值時（被用戶或被鏈接到它的約束器），它會喚醒所有相關的約束（除了剛剛喚醒的約束）來通知它們它得到了一個值。每個喚醒的約束之後會調查它的連接器，來看看是否有足夠的信息來為連接器求出一個值。如果可以，盒子會設置這個連接器，連接器之後會喚醒所有相關的約束，以此類推。例如，在攝氏溫度和華氏溫度的轉換中，w、x和y會被常量盒子9、5和32立即設置。連接器會喚醒乘法器和加法器，它們判斷出沒有足夠的信息用於處理。如果用戶（或者網絡的其它部分）將celsis連接器設置為某個值（比如25），最左邊的乘法器會被喚醒，之後它會將u設置為25 * 9 = 225。之後u會喚醒第二個乘法器，它會將v設置為45，之後v會喚醒加法器，它將fahrenheit連接器設置為77。

**使用約束系統。**為了使用約束系統來計算出上面所描述的溫度計算，我們首先創建了兩個具名連接器，celsius和fahrenheit，通過調用make_connector構造器。

>>> celsius = make_connector('Celsius')
>>> fahrenheit = make_connector('Fahrenheit')

之後，我們將這些連接器鏈接到網絡中，這個網絡反映了上面的圖示。函數make_converter組裝了網絡中不同的連接器和約束：

>>> def make_converter(c, f):
        """Connect c to f with constraints to convert from Celsius to Fahrenheit."""
        u, v, w, x, y = [make_connector() for _ in range(5)]
        multiplier(c, w, u)
        multiplier(v, x, u)
        adder(v, y, f)
        constant(w, 9)
        constant(x, 5)
        constant(y, 32)
>>> make_converter(celsius, fahrenheit)

我們會使用消息傳遞系統來協調約束和連接器。我們不會使用函數來響應消息，而是使用字典。用於分發的字典擁有字符串類型的鍵，代表它接受的消息。這些鍵關聯的值是這些消息的響應。

約束是不帶有局部狀態的字典。它們對消息的響應是非純函數，這些函數會改變所約束的連接器。

連接器是一個字典，持有當前值並響應操作該值的消息。約束不會直接改變連接器的值，而是會通過發送消息來改變，於是連接器可以提醒其他約束來響應變化。這樣，連接器代表了一個數值，同時封裝了連接器的行為。

我們可以發送給連接器的一種消息是設置它的值。這裡，我們（'user'）將celsius的值設置為25。

>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0

不僅僅是celsius的值變成了25，它的值也在網絡上傳播，於是fahrenheit的值也發生變化。這些變化打印了出來，因為我們在構造這兩個連接器的時候命名了它們。

現在我們可以試著將fahrenheit設置為新的值，比如212。

>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212

連接器報告說，它察覺到了一個矛盾：它的值是77.0，但是有人嘗試將其設置為212。如果我們真的想以新的值複用這個網絡，我們可以讓celsius忘掉舊的值。

>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgotten

連接器celsius發現了user，一開始設置了它的值，現在又想撤銷這個值，所以celsius同意丟掉這個值，並且通知了網絡的其餘部分。這個消息最終傳播給fahrenheit，它現在發現沒有理由繼續相信自己的值為77。於是，它也丟掉了它的值。

現在fahrenheit沒有值了，我們就可以將其設置為212：

>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0

這個新值在網絡上傳播，並強迫celsius持有值100。我們已經使用了非常相似的網絡，提供fahrenheit來計算celsius，以及提供celsius來計算fahrenheit。這個無方向的計算就是基於約束的網絡的特徵。

**實現約束系統。**像我們看到的那樣，連接器是字典，將消息名稱映射為函數和數據值。我們將要實現響應下列消息的連接器：

• connector['set_val'](source, value) 表示source請求連接器將當前值設置為該值。
• connector['has_val']() 返回連接器是否已經有了一個值。
• connector['val'] 是連接器的當前值。
• connector['forget'](source) 告訴連接器，source請求它忘掉當前值。
• connector['connect'](source) 告訴連接器參與新的約束source。

約束也是字典，接受來自連接器的以下兩種消息：

• constraint['new_val']() 表示連接到約束的連接器有了新的值。
• constraint['forget']() 表示連接到約束的連接器需要忘掉它的值。

當約束收到這些消息時，它們適當地將它們傳播給其它連接器。

adder函數在兩個連接器上構造了加法器約束，其中前兩個連接器必須加到第三個上：a + b = c。為了支持多方向的約束傳播，加法器必須也規定從c中減去a會得到b，或者從c中減去b會得到a。

>>> from operator import add, sub
>>> def adder(a, b, c):
        """The constraint that a + b = c."""
        return make_ternary_constraint(a, b, c, add, sub, sub)

我們希望實現一個通用的三元（三個方向）約束，它使用三個連接器和三個函數來創建約束，接受new_val和forget消息。消息的響應是局部函數，它放在叫做constraint的字典中。

>>> def make_ternary_constraint(a, b, c, ab, ca, cb):
        """The constraint that ab(a,b)=c and ca(c,a)=b and cb(c,b) = a."""
        def new_value():
            av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
            if av and bv:
                c['set_val'](constraint, ab(a['val'], b['val']))
            elif av and cv:
                b['set_val'](constraint, ca(c['val'], a['val']))
            elif bv and cv:
                a['set_val'](constraint, cb(c['val'], b['val']))
        def forget_value():
            for connector in (a, b, c):
                connector['forget'](constraint)
        constraint = {'new_val': new_value, 'forget': forget_value}
        for connector in (a, b, c):
            connector['connect'](constraint)
        return constraint

叫做constraint的字典是個分發字典，也是約束對象自身。它響應兩種約束接收到的消息，也在對連接器的調用中作為source參數傳遞。

無論約束什麼時候被通知，它的連接器之一擁有了值，約束的局部函數new_value都會被調用。這個函數首先檢查是否a和b都擁有值，如果是這樣，它告訴c將值設為函數ab的返回值，在adder中是add。約束，也就是adder對象，將自身作為source參數傳遞給連接器。如果a和b不同時擁有值，約束會檢查a和c，以此類推。

如果約束被通知，連接器之一忘掉了它的值，它會請求所有連接器忘掉它們的值（只有由約束設置的值會被真正丟掉）。

multiplier與adder類似：

>>> from operator import mul, truediv
>>> def multiplier(a, b, c):
        """The constraint that a * b = c."""
        return make_ternary_constraint(a, b, c, mul, truediv, truediv)

常量也是約束，但是它不會發送任何消息，因為它只包含一個單一的連接器，在構造的時候會設置它。

>>> def constant(connector, value):
        """The constraint that connector = value."""
        constraint = {}
        connector['set_val'](constraint, value)
        return constraint

這三個約束足以實現我們的溫度轉換網絡。

**表示連接器。**連接器表示為包含一個值的字典，但是同時擁有帶有局部狀態的響應函數。連接器必須跟蹤向它提供當前值的informant，以及它所參與的constraints列表。

構造器make_connector是局部函數，用於設置和忘掉值，它響應來自約束的消息。

>>> def make_connector(name=None):
        """A connector between constraints."""
        informant = None
        constraints = []
        def set_value(source, value):
            nonlocal informant
            val = connector['val']
            if val is None:
                informant, connector['val'] = source, value
                if name is not None:
                    print(name, '=', value)
                inform_all_except(source, 'new_val', constraints)
            else:
                if val != value:
                    print('Contradiction detected:', val, 'vs', value)
        def forget_value(source):
            nonlocal informant
            if informant == source:
                informant, connector['val'] = None, None
                if name is not None:
                    print(name, 'is forgotten')
                inform_all_except(source, 'forget', constraints)
        connector = {'val': None,
                     'set_val': set_value,
                     'forget': forget_value,
                     'has_val': lambda: connector['val'] is not None,
                     'connect': lambda source: constraints.append(source)}
        return connector

同時，連接器是一個分發字典，用於分發五個消息，約束使用它們來和連接器通信。前四個響應都是函數，最後一個響應就是值本身。

局部函數set_value在請求設置連接器的值時被調用。如果連接器當前並沒有值，它會設置該值並將informant記為請求設置該值的source約束。之後連接器會提醒所有參與的約束，除了請求設置該值的約束。這通過使用下列迭代函數來完成。

>>> def inform_all_except(source, message, constraints):
        """Inform all constraints of the message, except source."""
        for c in constraints:
            if c != source:
                c[message]()

如果一個連接器被請求忘掉它的值，它會調用局部函數forget_value，這個函數首先執行檢查，來確保請求來自之前設置該值的同一個約束。如果是的話，連接器通知相關的約束來丟掉當前值。

對has_val消息的響應表示連接器是否擁有一個值。對connect消息的響應將source約束添加到約束列表中。

我們設計的約束程序引入了許多出現在面向對象編程的概念。約束和連接器都是抽象，它們通過消息來操作。當連接器的值由消息改變時，消息不僅僅改變了它的值，還對其驗證（檢查來源）並傳播它的影響。實際上，在這一章的後面，我們會使用相似的字符串值的字典結構和函數值來實現面向對象系統。

2.5 面向對象編程

來源：2.5 Object-Oriented Programming

譯者：飛龍

協議：CC BY-NC-SA 4.0

面向對象編程（OOP）是一種用於組織程序的方法，它組合了這一章引入的許多概念。就像抽象數據類型那樣，對象創建了數據使用和實現之間的抽象界限。類似消息傳遞中的分發字典，對象響應行為請求。就像可變的數據結構，對象擁有局部狀態，並且不能直接從全局環境訪問。Python 對象系統提供了新的語法，更易於為組織程序實現所有這些實用的技巧。

但是對象系統不僅僅提供了便利；它也為程序設計添加了新的隱喻，其中程序中的幾個部分彼此交互。每個對象將局部狀態和行為綁定，以一種方式在數據抽象背後隱藏二者的複雜性。我們的約束程序的例子通過在約束和連接器之前傳遞消息，產生了這種隱喻。Python 對象系統使用新的途徑擴展了這種隱喻，來表達程序的不同部分如何互相關聯，以及互相通信。對象不僅僅會傳遞消息，還會和其它相同類型的對象共享行為，以及從相關的類型那裡繼承特性。

面向對象編程的範式使用自己的詞彙來強化對象隱喻。我們已經看到了，對象是擁有方法和屬性的數據值，可以通過點運算符來訪問。每個對象都擁有一個類型，叫做類。Python 中可以定義新的類，就像定義函數那樣。

2.5.1 對象和類

類可以用作所有類型為該類的對象的模板。每個對象都是某個特定類的實例。我們目前使用的對象都擁有內建類型，但是我們可以定義新的類，就像定義函數那樣。類的定義規定了在該類的對象之間共享的屬性和方法。我們會通過重新觀察銀行賬戶的例子，來介紹類的語句。

在介紹局部狀態時，我們看到，銀行賬戶可以自然地建模為擁有balance的可變值。銀行賬戶對象應該擁有withdraw方法，在可用的情況下，它會更新賬戶餘額，並返回所請求的金額。我們希望添加一些額外的行為來完善賬戶抽象：銀行賬戶應該能夠返回它的當前餘額，返回賬戶持有者的名稱，以及接受存款。

Account類允許我們創建銀行賬戶的多個實例。創建新對象實例的動作被稱為實例化該類。Python 中實例化某個類的語法類似於函數的調用語句。這裡，我們使用參數'Jim'（賬戶持有者的名稱）來調用Account。

>>> a = Account('Jim')

對象的屬性是和對象關聯的名值對，它可以通過點運算符來訪問。屬性特定於具體的對象，而不是類的所有對象，也叫做實例屬性。每個Account對象都擁有自己的餘額和賬戶持有者名稱，它們是實例屬性的一個例子。在更寬泛的編程社群中，實例屬性可能也叫做字段、屬性或者實例變量。

>>> a.holder
'Jim'
>>> a.balance
0

操作對象或執行對象特定計算的函數叫做方法。方法的副作用和返回值可能依賴或改變對象的其它屬性。例如，deposit是Account對象a上的方法。它接受一個參數，即需要存入的金額，修改對象的balance屬性，並返回產生的餘額。

>>> a.deposit(15)
15

在 OOP 中，我們說方法可以在特定對象上調用。作為調用withdraw方法的結果，要麼取錢成功，餘額減少並返回，要麼請求被拒絕，賬戶打印出錯誤信息。

>>> a.withdraw(10)  # The withdraw method returns the balance after withdrawal
5
>>> a.balance       # The balance attribute has changed
5
>>> a.withdraw(10)
'Insufficient funds'

像上面展示的那樣，方法的行為取決於對象屬性的改變。兩次以相同參數對withdraw的調用返回了不同的結果。

2.5.2 類的定義

用戶定義的類由class語句創建，它只包含單個子句。類的語句定義了類的名稱和基類（會在繼承那一節討論），之後包含了定義類屬性的語句組：

class <name>(<base class>):
    <suite>

當類的語句被執行時，新的類會被創建，並且在當前環境第一幀綁定到<name>上。之後會執行語句組。任何名稱都會在class語句的<suite>中綁定，通過def或賦值語句，創建或修改類的屬性。

類通常圍繞實例屬性來組織，實例屬性是名值對，不和類本身關聯但和類的每個對象關聯。通過為實例化新對象定義方法，類規定了它的對象的實例屬性。

class語句的<suite>部分包含def語句，它們為該類的對象定義了新的方法。用於實例化對象的方法在 Python 中擁有特殊的名稱，__init__（init兩邊分別有兩個下劃線），它叫做類的構造器。

>>> class Account(object):
        def __init__(self, account_holder):
            self.balance = 0
            self.holder = account_holder

Account的__init__方法有兩個形參。第一個是self，綁定到新創建的Account對象上。第二個參數，account_holder，在被調用來實例化的時候，綁定到傳給該類的參數上。

構造器將實例屬性名稱balance與0綁定。它也將屬性名稱holder綁定到account_holder上。形參account_holder是__init__方法的局部名稱。另一方面，通過最後一個賦值語句綁定的名稱holder是一直存在的，因為它使用點運算符被存儲為self的屬性。

定義了Account類之後，我們就可以實例化它：

>>> a = Account('Jim')

這個對Account類的“調用”創建了新的對象，它是Account的實例，之後以兩個參數調用了構造函數__init__：新創建的對象和字符串'Jim'。按照慣例，我們使用名稱self來命名構造器的第一個參數，因為它綁定到了被實例化的對象上。這個慣例在幾乎所有 Python 代碼中都適用。

現在，我們可以使用點運算符來訪問對象的balance和holder。

>>> a.balance
0
>>> a.holder
'Jim'

**身份。**每個新的賬戶實例都有自己的餘額屬性，它的值獨立於相同類的其它對象。

>>> b = Account('Jack')
>>> b.balance = 200
>>> [acc.balance for acc in (a, b)]
[0, 200]

為了強化這種隔離，每個用戶定義類的實例對象都有個獨特的身份。對象身份使用is和is not運算符來比較。

>>> a is a
True
>>> a is not b
True

雖然由同一個調用來構造，綁定到a和b的對象並不相同。通常，使用賦值將對象綁定到新名稱並不會創建新的對象。

>>> c = a
>>> c is a
True

用戶定義類的新對象只在類（比如Account）使用調用表達式被實例化的時候創建。

**方法。**對象方法也由class語句組中的def語句定義。下面，deposit和withdraw都被定義為Account類的對象上的方法：

>>> class Account(object):
        def __init__(self, account_holder):
            self.balance = 0
            self.holder = account_holder
        def deposit(self, amount):
            self.balance = self.balance + amount
            return self.balance
        def withdraw(self, amount):
            if amount > self.balance:
                return 'Insufficient funds'
            self.balance = self.balance - amount
            return self.balance

雖然方法定義和函數定義在聲明方式上並沒有區別，方法定義有不同的效果。由class語句中的def語句創建的函數值綁定到了聲明的名稱上，但是隻在類的局部綁定為一個屬性。這個值可以使用點運算符在類的實例上作為方法來調用。

每個方法定義同樣包含特殊的首個參數self，它綁定到方法所調用的對象上。例如，讓我們假設deposit在特定的Account對象上調用，並且傳遞了一個對象值：要存入的金額。對象本身綁定到了self上，而參數綁定到了amount上。所有被調用的方法能夠通過self參數來訪問對象，所以它們可以訪問並操作對象的狀態。

為了調用這些方法，我們再次使用點運算符，就像下面這樣：

>>> tom_account = Account('Tom')
>>> tom_account.deposit(100)
100
>>> tom_account.withdraw(90)
10
>>> tom_account.withdraw(90)
'Insufficient funds'
>>> tom_account.holder
'Tom'

當一個方法通過點運算符調用時，對象本身（這個例子中綁定到了tom_account）起到了雙重作用。首先，它決定了withdraw意味著哪個名稱；withdraw並不是環境中的名稱，而是Account類局部的名稱。其次，當withdraw方法調用時，它綁定到了第一個參數self上。求解點運算符的詳細過程會在下一節中展示。

2.5.3 消息傳遞和點表達式

方法定義在類中，而實例屬性通常在構造器中賦值，二者都是面向對象編程的基本元素。這兩個概念很大程度上類似於數據值的消息傳遞實現中的分發字典。對象使用點運算符接受消息，但是消息並不是任意的、值為字符串的鍵，而是類的局部名稱。對象也擁有具名的局部狀態值（實例屬性），但是這個狀態可以使用點運算符訪問和操作，並不需要在實現中使用nonlocal語句。

消息傳遞的核心概念，就是數據值應該通過響應消息而擁有行為，這些消息和它們所表示的抽象類型相關。點運算符是 Python 的語法特徵，它形成了消息傳遞的隱喻。使用帶有內建對象系統語言的優點是，消息傳遞能夠和其它語言特性，例如賦值語句無縫對接。我們並不需要不同的消息來“獲取”和“設置”關聯到局部屬性名稱的值；語言的語法允許我們直接使用消息名稱。

**點表達式。**類似tom_account.deposit的代碼片段叫做點表達式。點表達式包含一個表達式，一個點和一個名稱：

<expression> . <name>

<expression>可為任意的 Python 有效表達式，但是<name>必須是個簡單的名稱（而不是求值為name的表達式）。點表達式會使用提供的<name>，對值為<expression>的對象求出屬性的值。

內建的函數getattr也會按名稱返回對象的屬性。它是等價於點運算符的函數。使用getattr，我們就能使用字符串來查找某個屬性，就像分發字典那樣：

>>> getattr(tom_account, 'balance')
10

我們也可以使用hasattr測試對象是否擁有某個具名屬性：

>>> hasattr(tom_account, 'deposit')
True

對象的屬性包含所有實例屬性，以及所有定義在類中的屬性（包括方法）。方法是需要特別處理的類的屬性。

**方法和函數。**當一個方法在對象上調用時，對象隱式地作為第一個參數傳遞給方法。也就是說，點運算符左邊值為<expression>的對象，會自動傳給點運算符右邊的方法，作為第一個參數。所以，對象綁定到了參數self上。

為了自動實現self的綁定，Python 區分函數和綁定方法。我們已經在這門課的開始創建了前者，而後者在方法調用時將對象和函數組合到一起。綁定方法的值已經將第一個函數關聯到所調用的實例，當方法調用時實例會被命名為self。

通過在點運算符的返回值上調用type，我們可以在交互式解釋器中看到它們的差異。作為類的屬性，方法只是個函數，但是作為實例屬性，它是綁定方法：

>>> type(Account.deposit)
<class 'function'>
>>> type(tom_account.deposit)
<class 'method'>

這兩個結果的唯一不同點是，前者是個標準的二元函數，帶有參數self和amount。後者是一元方法，當方法被調用時，名稱self自動綁定到了名為tom_account的對象上，而名稱amount會被綁定到傳遞給方法的參數上。這兩個值，無論函數值或綁定方法的值，都和相同的deposit函數體所關聯。

我們可以以兩種方式調用deposit：作為函數或作為綁定方法。在前者的例子中，我們必須為self參數顯式提供實參。而對於後者，self參數已經自動綁定了。

>>> Account.deposit(tom_account, 1001)  # The deposit function requires 2 arguments
1011
>>> tom_account.deposit(1000)           # The deposit method takes 1 argument
2011

函數getattr的表現就像運算符那樣：它的第一個參數是對象，而第二個參數（名稱）是定義在類中的方法。之後，getattr返回綁定方法的值。另一方面，如果第一個參數是個類，getattr會直接返回屬性值，它僅僅是個函數。

**實踐指南：命名慣例。**類名稱通常以首字母大寫來編寫（也叫作駝峰拼寫法，因為名稱中間的大寫字母像駝峰）。方法名稱遵循函數命名的慣例，使用以下劃線分隔的小寫字母。

有的時候，有些實例變量和方法的維護和對象的一致性相關，我們不想讓用戶看到或使用它們。它們並不是由類定義的一部分抽象，而是一部分實現。Python 的慣例規定，如果屬性名稱以下劃線開始，它只能在方法或類中訪問，而不能被類的用戶訪問。

2.5.4 類屬性

有些屬性值在特定類的所有對象之間共享。這樣的屬性關聯到類本身，而不是類的任何獨立實例。例如，讓我們假設銀行以固定的利率對餘額支付利息。這個利率可能會改變，但是它是在所有賬戶中共享的單一值。

類屬性由class語句組中的賦值語句創建，位於任何方法定義之外。在更寬泛的開發者社群中，類屬性也被叫做類變量或靜態變量。下面的類語句以名稱interest為Account創建了類屬性。

>>> class Account(object):
        interest = 0.02            # A class attribute
        def __init__(self, account_holder):
            self.balance = 0
            self.holder = account_holder
        # Additional methods would be defined here

這個屬性仍舊可以通過類的任何實例來訪問。

>>> tom_account = Account('Tom')
>>> jim_account = Account('Jim')
>>> tom_account.interest
0.02
>>> jim_account.interest
0.02

但是，對類屬性的單一賦值語句會改變所有該類實例上的屬性值。

>>> Account.interest = 0.04
>>> tom_account.interest
0.04
>>> jim_account.interest
0.04

**屬性名稱。**我們已經在我們的對象系統中引入了足夠的複雜性，我們需要規定名稱如何解析為特定的屬性。畢竟，我們可以輕易擁有同名的類屬性和實例屬性。

像我們看到的那樣，點運算符由表達式、點和名稱組成：

<expression> . <name>

為了求解點表達式：

1. 求出點左邊的<expression>，會產生點運算符的對象。
2. <name>會和對象的實例屬性匹配；如果該名稱的屬性存在，會返回它的值。
3. 如果<name>不存在於實例屬性，那麼會在類中查找<name>，這會產生類的屬性值。
4. 這個值會被返回，如果它是個函數，則會返回綁定方法。

在這個求值過程中，實例屬性在類的屬性之前查找，就像局部名稱具有高於全局的優先級。定義在類中的方法，在求值過程的第三步綁定到了點運算符的對象上。在類中查找名稱的過程有額外的差異，在我們引入類繼承的時候就會出現。

**賦值。**所有包含點運算符的賦值語句都會作用於右邊的對象。如果對象是個實例，那麼賦值就會設置實例屬性。如果對象是個類，那麼賦值會設置類屬性。作為這條規則的結果，對對象屬性的賦值不能影響類的屬性。下面的例子展示了這個區別。

如果我們向賬戶實例的具名屬性interest賦值，我們會創建屬性的新實例，它和現有的類屬性具有相同名稱。

>>> jim_account.interest = 0.08

這個屬性值會通過點運算符返回：

>>> jim_account.interest
0.08

但是，類屬性interest會保持為原始值，它可以通過所有其他賬戶返回。

>>> tom_account.interest
0.04

類屬性interest的改動會影響tom_account，但是jim_account的實例屬性不受影響。

>>> Account.interest = 0.05  # changing the class attribute
>>> tom_account.interest     # changes instances without like-named instance attributes
0.05
>>> jim_account.interest     # but the existing instance attribute is unaffected
0.08

2.5.5 繼承

在使用 OOP 範式時，我們通常會發現，不同的抽象數據結構是相關的。特別是，我們發現相似的類在特化的程度上有區別。兩個類可能擁有相似的屬性，但是一個表示另一個的特殊情況。

例如，我們可能希望實現一個活期賬戶，它不同於標準的賬戶。活期賬戶對每筆取款都收取額外的 $1，並且具有較低的利率。這裡，我們演示上述行為：

>>> ch = CheckingAccount('Tom')
>>> ch.interest     # Lower interest rate for checking accounts
0.01
>>> ch.deposit(20)  # Deposits are the same
20
>>> ch.withdraw(5)  # withdrawals decrease balance by an extra charge
14

CheckingAccount是Account的特化。在 OOP 的術語中，通用的賬戶會作為CheckingAccount的基類，而CheckingAccount是Account的子類（術語“父類”和“超類”通常等同於“基類”，而“派生類”通常等同於“子類”）。

子類繼承了基類的屬性，但是可能覆蓋特定屬性，包括特定的方法。使用繼承，我們只需要關注基類和子類之間有什麼不同。任何我們在子類未指定的東西會自動假設和基類中相同。

繼承也在對象隱喻中有重要作用，不僅僅是一種實用的組織方式。繼承意味著在類之間表達“is-a”關係，它和“has-a”關係相反。活期賬戶是（is-a）一種特殊類型的賬戶，所以讓CheckingAccount繼承Account是繼承的合理使用。另一方面，銀行擁有（has-a）所管理的銀行賬戶的列表，所以二者都不應繼承另一個。反之，賬戶對象的列表應該自然地表現為銀行賬戶的實例屬性。

2.5.6 使用繼承

我們通過將基類放置到類名稱後面的圓括號內來指定繼承。首先，我們提供Account類的完整實現，也包含類和方法的文檔字符串。

>>> class Account(object):
        """A bank account that has a non-negative balance."""
        interest = 0.02
        def __init__(self, account_holder):
            self.balance = 0
            self.holder = account_holder
        def deposit(self, amount):
            """Increase the account balance by amount and return the new balance."""
            self.balance = self.balance + amount
            return self.balance
        def withdraw(self, amount):
            """Decrease the account balance by amount and return the new balance."""
            if amount > self.balance:
                return 'Insufficient funds'
            self.balance = self.balance - amount
            return self.balance

CheckingAccount的完整實現在下面：

>>> class CheckingAccount(Account):
        """A bank account that charges for withdrawals."""
        withdraw_charge = 1
        interest = 0.01
        def withdraw(self, amount):
            return Account.withdraw(self, amount + self.withdraw_charge)

這裡，我們引入了類屬性withdraw_charge，它特定於CheckingAccount類。我們將一個更低的值賦給interest屬性。我們也定義了新的withdraw方法來覆蓋定義在Account對象中的行為。類語句組中沒有更多的語句，所有其它行為都從基類Account中繼承。

>>> checking = CheckingAccount('Sam')
>>> checking.deposit(10)
10
>>> checking.withdraw(5)
4
>>> checking.interest
0.01

checking.deposit表達式是用於存款的綁定方法，它定義在Account類中，當 Python 解析點表達式中的名稱時，實例上並沒有這個屬性，它會在類中查找該名稱。實際上，在類中“查找名稱”的行為會在原始對象的類的繼承鏈中的每個基類中查找。我們可以遞歸定義這個過程，為了在類中查找名稱：

1. 如果類中有帶有這個名稱的屬性，返回屬性值。
2. 否則，如果有基類的話，在基類中查找該名稱。

在deposit中，Python 會首先在實例中查找名稱，之後在CheckingAccount類中。最後，它會在Account中查找，這裡是deposit定義的地方。根據我們對點運算符的求值規則，由於deposit是在checking實例的類中查找到的函數，點運算符求值為綁定方法。這個方法以參數10調用，這會以綁定到checking對象的self和綁定到10的amount調用deposit方法。

對象的類會始終保持不變。即使deposit方法在Account類中找到，deposit以綁定到CheckingAccount實例的self調用，而不是Account的實例。

譯者注：CheckingAccount的實例也是Account的實例，這個說法是有問題的。

**調用祖先。**被覆蓋的屬性仍然可以通過類對象來訪問。例如，我們可以通過以包含withdraw_charge的參數調用Account的withdraw方法，來實現CheckingAccount的withdraw方法。

要注意我們調用self.withdraw_charge而不是等價的CheckingAccount.withdraw_charge。前者的好處就是繼承自CheckingAccount的類可能會覆蓋支取費用。如果是這樣的話，我們希望我們的withdraw實現使用新的值而不是舊的值。

2.5.7 多重繼承

Python 支持子類從多個基類繼承屬性的概念，這是一種叫做多重繼承的語言特性。

假設我們從Account繼承了SavingsAccount，每次存錢的時候向客戶收取一筆小費用。

>>> class SavingsAccount(Account):
        deposit_charge = 2
        def deposit(self, amount):
            return Account.deposit(self, amount - self.deposit_charge)

之後，一個聰明的總經理設想了AsSeenOnTVAccount，它擁有CheckingAccount和SavingsAccount的最佳特性：支取和存入的費用，以及較低的利率。它將儲蓄賬戶和活期存款賬戶合二為一！“如果我們構建了它”，總經理解釋道，“一些人會註冊並支付所有這些費用。甚至我們會給他們一美元。”

>>> class AsSeenOnTVAccount(CheckingAccount, SavingsAccount):
        def __init__(self, account_holder):
            self.holder = account_holder
            self.balance = 1           # A free dollar!

實際上，這個實現就完整了。存款和取款都需要費用，使用了定義在CheckingAccount和SavingsAccount中的相應函數。

>>> such_a_deal = AsSeenOnTVAccount("John")
>>> such_a_deal.balance
1
>>> such_a_deal.deposit(20)            # $2 fee from SavingsAccount.deposit
19
>>> such_a_deal.withdraw(5)            # $1 fee from CheckingAccount.withdraw
13

就像預期那樣，沒有歧義的引用會正確解析：

>>> such_a_deal.deposit_charge
2
>>> such_a_deal.withdraw_charge
1

但是如果引用有歧義呢，比如withdraw方法的引用，它定義在Account和CheckingAccount中？下面的圖展示了AsSeenOnTVAccount類的繼承圖。每個箭頭都從子類指向基類。

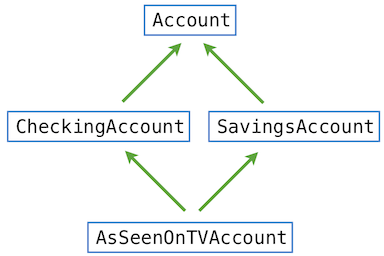
對於像這樣的簡單“菱形”，Python 從左到右解析名稱，之後向上。這個例子中，Python 按下列順序檢查名稱，直到找到了具有該名稱的屬性：

AsSeenOnTVAccount, CheckingAccount, SavingsAccount, Account, object

繼承順序的問題沒有正確的解法，因為我們可能會給某個派生類高於其他類的優先級。但是，任何支持多重繼承的編程語言必須始終選擇同一個順序，便於語言的用戶預測程序的行為。

**擴展閱讀。**Python 使用一種叫做 C3 Method Resolution Ordering 的遞歸算法來解析名稱。任何類的方法解析順序都使用所有類上的mro方法來查詢。

>>> [c.__name__ for c in AsSeenOnTVAccount.mro()]
['AsSeenOnTVAccount', 'CheckingAccount', 'SavingsAccount', 'Account', 'object']

這個用於查詢方法解析順序的算法並不是這門課的主題，但是 Python 的原作者使用一篇原文章的引用來描述它。

2.5.8 對象的作用

Python 對象系統為使數據抽象和消息傳遞更加便捷和靈活而設計。類、方法、繼承和點運算符的特化語法都可以讓我們在程序中形成對象隱喻，它能夠提升我們組織大型程序的能力。

特別是，我們希望我們的對象系統在不同層面上促進關注分離。每個程序中的對象都封裝和管理程序狀態的一部分，每個類語句都定義了一些函數，它們實現了程序總體邏輯的一部分。抽象界限強制了大型程序不同層面之間的邊界。

面向對象編程適合於對系統建模，這些系統擁有相互分離並交互的部分。例如，不同用戶在社交網絡中互動，不同角色在遊戲中互動，以及不同圖形在物理模擬中互動。在表現這種系統的時候，程序中的對象通常自然地映射為被建模系統中的對象，類用於表現它們的類型和關係。

另一方面，類可能不會提供用於實現特定的抽象的最佳機制。函數式抽象提供了更加自然的隱喻，用於表現輸入和輸出的關係。一個人不應該強迫自己把程序中的每個細微的邏輯都塞到類裡面，尤其是當定義獨立函數來操作數據變得十分自然的時候。函數也強制了關注分離。

類似 Python 的多範式語言允許程序員為合適的問題匹配合適的範式。為了簡化程序，或使程序模塊化，確定何時引入新的類，而不是新的函數，是軟件工程中的重要設計技巧，這需要仔細關注。

2.6 實現類和對象

來源：2.6 Implementing Classes and Objects

譯者：飛龍

協議：CC BY-NC-SA 4.0

在使用面向對象編程範式時，我們使用對象隱喻來指導程序的組織。數據表示和操作的大部分邏輯都表達在類的定義中。在這一節中，我們會看到，類和對象本身可以使用函數和字典來表示。以這種方式實現對象系統的目的是展示使用對象隱喻並不需要特殊的編程語言。即使編程語言沒有面向對象系統，程序照樣可以面向對象。

為了實現對象，我們需要拋棄點運算符（它需要語言的內建支持），並創建分發字典，它的行為和內建對象系統的元素差不多。我們已經看到如何通過分發字典實現消息傳遞行為。為了完整實現對象系統，我們需要在實例、類和基類之間發送消息，它們全部都是含有屬性的字典。

我們不會實現整個 Python 對象系統，它包含這篇文章沒有涉及到的特性（比如元類和靜態方法）。我們會專注於用戶定義的類，不帶有多重繼承和內省行為（比如返回實例的類）。我們的實現並不遵循 Python 類型系統的明確規定。反之，它為實現對象隱喻的核心功能而設計。

2.6.1 實例

我們從實例開始。實例擁有具名屬性，例如賬戶餘額，它可以被設置或獲取。我們使用分發字典來實現實例，它會響應“get”和“set”屬性值消息。屬性本身保存在叫做attributes的局部字典中。

就像我們在這一章的前面看到的那樣，字典本身是抽象數據類型。我們使用列表來實現字典，我們使用偶對來實現列表，並且我們使用函數來實現偶對。就像我們以字典實現對象系統那樣，要注意我們能夠僅僅使用函數來實現對象。

為了開始我們的實現，我們假設我們擁有一個類實現，它可以查找任何不是實例部分的名稱。我們將類作為參數cls傳遞給make_instance。

>>> def make_instance(cls):
        """Return a new object instance, which is a dispatch dictionary."""
        def get_value(name):
            if name in attributes:
                return attributes[name]
            else:
                value = cls['get'](name)
                return bind_method(value, instance)
        def set_value(name, value):
            attributes[name] = value
        attributes = {}
        instance = {'get': get_value, 'set': set_value}
        return instance

instance是分發字典，它響應消息get和set。set消息對應 Python 對象系統的屬性賦值：所有賦值的屬性都直接儲存在對象的局部屬性字典中。在get中，如果name在局部attributes字典中不存在，那麼它會在類中尋找。如果cls返回的value為函數，它必須綁定到實例上。

綁定方法值。make_instance中的get_value 使用get尋找類中的具名屬性，之後調用bind_method。方法的綁定只在函數值上調用，並且它會通過將實例插入為第一個參數，從函數值創建綁定方法的值。

>>> def bind_method(value, instance):
        """Return a bound method if value is callable, or value otherwise."""
        if callable(value):
            def method(*args):
                return value(instance, *args)
            return method
        else:
            return value

當方法被調用時，第一個參數self通過這個定義綁定到了instance的值上。

2.6.2 類

類也是對象，在 Python 對象系統和我們這裡實現的系統中都是如此。為了簡化，我們假設類自己並沒有類（在 Python 中，類本身也有類，幾乎所有類都共享相同的類，叫做type）。類可以接受get和set消息，以及new消息。

>>> def make_class(attributes, base_class=None):
        """Return a new class, which is a dispatch dictionary."""
        def get_value(name):
            if name in attributes:
                return attributes[name]
            elif base_class is not None:
                return base_class['get'](name)
        def set_value(name, value):
            attributes[name] = value
        def new(*args):
            return init_instance(cls, *args)
        cls = {'get': get_value, 'set': set_value, 'new': new}
        return cls

不像實例那樣，類的get函數在屬性未找到的時候並不查詢它的類，而是查詢它的base_class。類並不需要方法綁定。

實例化。make_class 中的new函數調用了init_instance，它首先創建新的實例，之後調用叫做__init__的方法。

>>> def init_instance(cls, *args):
        """Return a new object with type cls, initialized with args."""
        instance = make_instance(cls)
        init = cls['get']('__init__')
        if init:
            init(instance, *args)
        return instance

最後這個函數完成了我們的對象系統。我們現在擁有了實例，它的set是局部的，但是get會回溯到它們的類中。實例在它的類中查找名稱之後，它會將自己綁定到函數值上來創建方法。最後類可以創建新的（new）實例，並且在實例創建之後立即調用它們的__init__構造器。

在對象系統中，用戶僅僅可以調用create_class，所有其他功能通過消息傳遞來使用。與之相似，Python 的對象系統由class語句來調用，它的所有其他功能都通過點表達式和對類的調用來使用。

2.6.3 使用所實現的對象

我們現在回到上一節銀行賬戶的例子。使用我們實現的對象系統，我們就可以創建Account類，CheckingAccount子類和它們的實例。

Account類通過create_account_class 函數創建，它擁有類似於 Python class語句的結構，但是以make_class的調用結尾。

>>> def make_account_class():
        """Return the Account class, which has deposit and withdraw methods."""
        def __init__(self, account_holder):
            self['set']('holder', account_holder)
            self['set']('balance', 0)
        def deposit(self, amount):
            """Increase the account balance by amount and return the new balance."""
            new_balance = self['get']('balance') + amount
            self['set']('balance', new_balance)
            return self['get']('balance')
        def withdraw(self, amount):
            """Decrease the account balance by amount and return the new balance."""
            balance = self['get']('balance')
            if amount > balance:
                return 'Insufficient funds'
            self['set']('balance', balance - amount)
            return self['get']('balance')
        return make_class({'__init__': __init__,
                           'deposit':  deposit,
                           'withdraw': withdraw,
                           'interest': 0.02})

在這個函數中，屬性名稱在最後設置。不像 Python 的class語句，它強制內部函數和屬性名稱之間的一致性。這裡我們必須手動指定屬性名稱和值的對應關係。

Account類最終由賦值來實例化。

>>> Account = make_account_class()

之後，賬戶實例通過new消息來創建，它需要名稱來處理新創建的賬戶。

>>> jim_acct = Account['new']('Jim')

之後，get消息傳遞給jim_acct ，來獲取屬性和方法。方法可以調用來更新賬戶餘額。

>>> jim_acct['get']('holder')
'Jim'
>>> jim_acct['get']('interest')
0.02
>>> jim_acct['get']('deposit')(20)
20
>>> jim_acct['get']('withdraw')(5)
15

就像使用 Python 對象系統那樣，設置實例的屬性並不會修改類的對應屬性：

>>> jim_acct['set']('interest', 0.04)
>>> Account['get']('interest')
0.02

**繼承。**我們可以創建CheckingAccount子類，通過覆蓋類屬性的子集。在這裡，我們修改withdraw方法來收取費用，並且降低了利率。

>>> def make_checking_account_class():
        """Return the CheckingAccount class, which imposes a $1 withdrawal fee."""
        def withdraw(self, amount):
            return Account['get']('withdraw')(self, amount + 1)
        return make_class({'withdraw': withdraw, 'interest': 0.01}, Account)

在這個實現中，我們在子類的withdraw 中調用了基類Account的withdraw函數，就像在 Python 內建對象系統那樣。我們可以創建子類本身和它的實例，就像之前那樣：

>>> CheckingAccount = make_checking_account_class()
>>> jack_acct = CheckingAccount['new']('Jack')

它們的行為相似，構造函數也一樣。每筆取款都會在特殊的withdraw函數中收費 $1，並且interest也擁有新的較低值。

>>> jack_acct['get']('interest')
0.01
>>> jack_acct['get']('deposit')(20)
20
>>> jack_acct['get']('withdraw')(5)
14

我們的構建在字典上的對象系統十分類似於 Python 內建對象系統的實現。Python 中，任何用戶定義類的實例，都有個特殊的__dict__屬性，將對象的局部實例屬性儲存在字典中，就像我們的attributes字典那樣。Python 的區別在於，它區分特定的特殊方法，這些方法和內建函數交互來確保那些函數能正常處理許多不同類型的參數。操作不同類型參數的函數是下一節的主題。

2.7 泛用方法

來源：2.7 Generic Operations

譯者：飛龍

協議：CC BY-NC-SA 4.0

這一章中我們引入了複合數據類型，以及由構造器和選擇器實現的數據抽象機制。使用消息傳遞，我們就能使抽象數據類型直接擁有行為。使用對象隱喻，我們可以將數據的表示和用於操作數據的方法綁定在一起，從而使數據驅動的程序模塊化，並帶有局部狀態。

但是，我們仍然必須展示，我們的對象系統允許我們在大型程序中靈活組合不同類型的對象。點運算符的消息傳遞僅僅是一種用於使用多個對象構建組合表達式的方式。這一節中，我們會探索一些用於組合和操作不同類型對象的方式。

2.7.1 字符串轉換

我們在這一章最開始說，對象值的行為應該類似它所表達的數據，包括產生它自己的字符串表示。數據值的字符串表示在類似 Python 的交互式語言中尤其重要，其中“讀取-求值-打印”的循環需要每個值都擁有某種字符串表示形式。

字符串值為人們的信息交流提供了基礎的媒介。字符序列可以在屏幕上渲染，打印到紙上，大聲朗讀，轉換為盲文，或者以莫爾茲碼廣播。字符串對編程而言也非常基礎，因為它們可以表示 Python 表達式。對於一個對象，我們可能希望生成一個字符串，當作為 Python 表達式解釋時，求值為等價的對象。

Python 規定，所有對象都應該能夠產生兩種不同的字符串表示：一種是人類可解釋的文本，另一種是 Python 可解釋的表達式。字符串的構造函數str返回人類可讀的字符串。在可能的情況下，repr函數返回一個 Python 表達式，它可以求值為等價的對象。repr的文檔字符串解釋了這個特性：

repr(object) -> string

Return the canonical string representation of the object.
For most object types, eval(repr(object)) == object.

在表達式的值上調用repr的結果就是 Python 在交互式會話中打印的東西。

>>> 12e12
12000000000000.0
>>> print(repr(12e12))
12000000000000.0

在不存在任何可以求值為原始值的表達式的情況中，Python 會產生一個代理：

>>> repr(min)
'<built-in function min>'

str構造器通常與repr相同，但是有時會提供更加可解釋的文本表示。例如，我們可以看到str和repr對於日期的不同：

>>> from datetime import date
>>> today = date(2011, 9, 12)
>>> repr(today)
'datetime.date(2011, 9, 12)'
>>> str(today)
'2011-09-12'

repr函數的定義出現了新的挑戰：我們希望它對所有數據類型都正確應用，甚至是那些在repr實現時還不存在的類型。我們希望它像一個多態函數，可以作用於許多（多）不同形式（態）的數據。

消息傳遞提供了這個問題的解決方案：repr函數在參數上調用叫做__repr__的函數。

>>> today.__repr__()
'datetime.date(2011, 9, 12)'

通過在用戶定義的類上實現同一方法，我們就可以將repr的適用性擴展到任何我們以後創建的類。這個例子強調了消息傳遞的另一個普遍的好處：就是它提供了一種機制，用於將現有函數的職責範圍擴展到新的對象。

str構造器以類似的方式實現：它在參數上調用了叫做__str__的方法。

>>> today.__str__()
'2011-09-12'

這些多態函數是一個更普遍原則的例子：特定函數應該作用於多種數據類型。這裡舉例的消息傳遞方法僅僅是多態函數實現家族的一員。本節剩下的部分會探索一些備選方案。

2.7.2 多重表示

使用對象或函數的數據抽象是用於管理複雜性的強大工具。抽象數據類型允許我們在數據表示和用於操作數據的函數之間構造界限。但是，在大型程序中，對於程序中的某種數據類型，提及“底層表示”可能不總是有意義。首先，一個數據對象可能有多種實用的表示，而且我們可能希望設計能夠處理多重表示的系統。

為了選取一個簡單的示例，複數可以用兩種幾乎等價的方式來表示：直角座標（虛部和實部）以及極座標（模和角度）。有時直角座標形式更加合適，而有時極座標形式更加合適。複數以兩種方式表示，而操作複數的函數可以處理每種表示，這樣一個系統確實比較合理。

更重要的是，大型軟件系統工程通常由許多人設計，並花費大量時間，需求的主題隨時間而改變。在這樣的環境中，每個人都事先同意數據表示的方案是不可能的。除了隔離使用和表示的數據抽象的界限，我們需要隔離不同設計方案的界限，以及允許不同方案在一個程序中共存。進一步，由於大型程序通常通過組合已存在的模塊創建，這些模塊會單獨設計，我們需要一種慣例，讓程序員將模塊遞增地組合為大型系統。也就是說，不需要重複設計或實現這些模塊。

我們以最簡單的複數示例開始。我們會看到，消息傳遞在維持“複數”對象的抽象概念時，如何讓我們為複數的表示設計出分離的直角座標和極座標表示。我們會通過使用泛用選擇器為複數定義算數函數（add_complex，mul_complex）來完成它。泛用選擇器可訪問複數的一部分，獨立於數值表示的方式。所產生的複數系統包含兩種不同類型的抽象界限。它們隔離了高階操作和低階表示。此外，也有一個垂直的界限，它使我們能夠獨立設計替代的表示。

作為邊注，我們正在開發一個系統，它在複數上執行算數運算，作為一個簡單但不現實的使用泛用操作的例子。複數類型實際上在 Python 中已經內建了，但是這個例子中我們仍然自己實現。

就像有理數那樣，複數可以自然表示為偶對。複數集可以看做帶有兩個正交軸，實數軸和虛數軸的二維空間。根據這個觀點，複數z = x + y * i（其中i*i = -1）可以看做平面上的點，它的實數為x，虛部為y。複數加法涉及到將它們的實部和虛部相加。

對複數做乘法時，將複數以極座標表示為模和角度更加自然。兩個複數的乘積是，將一個複數按照另一個的長度作為因數拉伸，之後按照另一個的角度來旋轉它的所得結果。

所以，複數有兩種不同表示，它們適用於不同的操作。然而，從一些人編寫使用複數的程序的角度來看，數據抽象的原則表明，所有操作複數的運算都應該可用，無論計算機使用了哪個表示。

**接口。**消息傳遞並不僅僅提供用於組裝行為和數據的方式。它也允許不同的數據類型以不同方式響應相同消息。來自不同對象，產生相似行為的共享消息是抽象的有力手段。

像之前看到的那樣，抽象數據類型由構造器、選擇器和額外的行為條件定義。與之緊密相關的概念是接口，它是共享消息的集合，帶有它們含義的規定。響應__repr__和__str__特殊方法的對象都實現了通用的接口，它們可以表示為字符串。

在複數的例子中，接口需要實現由四個消息組成的算數運算：real，imag，magnitude和angle。我們可以使用這些消息實現加法和乘法。

我們擁有兩種複數的抽象數據類型，它們的構造器不同。

• ComplexRI從實部和虛部構造複數。
• ComplexMA從模和角度構造複數。

使用這些消息和構造器，我們可以實現複數算數：

>>> def add_complex(z1, z2):
        return ComplexRI(z1.real + z2.real, z1.imag + z2.imag)
>>> def mul_complex(z1, z2):
        return ComplexMA(z1.magnitude * z2.magnitude, z1.angle + z2.angle)

術語“抽象數據類型”（ADT）和“接口”的關係是微妙的。ADT 包含構建複雜數據類的方式，以單元操作它們，並且可以選擇它們的組件。在面向對象系統中，ADT 對應一個類，雖然我們已經看到對象系統並不需要實現 ADT。接口是一組與含義關聯的消息，並且它可能包含選擇器，也可能不包含。概念上，ADT 描述了一類東西的完整抽象表示，而接口規定了可能在許多東西之間共享的行為。

**屬性（Property）。**我們希望交替使用複數的兩種類型，但是對於每個數值來說，儲存重複的信息比較浪費。我們希望儲存實部-虛部的表示或模-角度的表示之一。

Python 擁有一個簡單的特性，用於從零個參數的函數憑空計算屬性（Attribute）。@property裝飾器允許函數不使用標準調用表達式語法來調用。根據實部和虛部的複數實現展示了這一點。

>>> from math import atan2
>>> class ComplexRI(object):
        def __init__(self, real, imag):
            self.real = real
            self.imag = imag
        @property
        def magnitude(self):
            return (self.real ** 2 + self.imag ** 2) ** 0.5
        @property
        def angle(self):
            return atan2(self.imag, self.real)
        def __repr__(self):
            return 'ComplexRI({0}, {1})'.format(self.real, self.imag)

第二種使用模和角度的實現提供了相同接口，因為它響應同一組消息。

>>> from math import sin, cos
>>> class ComplexMA(object):
        def __init__(self, magnitude, angle):
            self.magnitude = magnitude
            self.angle = angle
        @property
        def real(self):
            return self.magnitude * cos(self.angle)
        @property
        def imag(self):
            return self.magnitude * sin(self.angle)
        def __repr__(self):
            return 'ComplexMA({0}, {1})'.format(self.magnitude, self.angle)

實際上，我們的add_complex和mul_complex實現並沒有完成；每個複數類可以用於任何算數函數的任何參數。對象系統不以任何方式顯式連接（例如通過繼承）這兩種複數類型，這需要給個註解。我們已經通過在兩個類之間共享一組通用的消息和接口，實現了複數抽象。

>>> from math import pi
>>> add_complex(ComplexRI(1, 2), ComplexMA(2, pi/2))
ComplexRI(1.0000000000000002, 4.0)
>>> mul_complex(ComplexRI(0, 1), ComplexRI(0, 1))
ComplexMA(1.0, 3.141592653589793)

編碼多種表示的接口擁有良好的特性。用於每個表示的類可以獨立開發；它們只需要遵循它們所共享的屬性名稱。這個接口同時是遞增的。如果另一個程序員希望向相同程序添加第三個複數表示，它們只需要使用相同屬性創建另一個類。

**特殊方法。**內建的算數運算符可以以一種和repr相同的方式擴展；它們是特殊的方法名稱，對應 Python 的算數、邏輯和序列運算的運算符。

為了使我們的代碼更加易讀，我們可能希望在執行復數加法和乘法時直接使用+和*運算符。將下列方法添加到兩個複數類中，這會讓這些運算符，以及opertor模塊中的add和mul函數可用。

>>> ComplexRI.__add__ = lambda self, other: add_complex(self, other)
>>> ComplexMA.__add__ = lambda self, other: add_complex(self, other)
>>> ComplexRI.__mul__ = lambda self, other: mul_complex(self, other)
>>> ComplexMA.__mul__ = lambda self, other: mul_complex(self, other)

現在，我們可以對我們的自定義類使用中綴符號。

>>> ComplexRI(1, 2) + ComplexMA(2, 0)
ComplexRI(3.0, 2.0)
>>> ComplexRI(0, 1) * ComplexRI(0, 1)
ComplexMA(1.0, 3.141592653589793)

**擴展閱讀。**為了求解含有+運算符的表達式，Python 會檢查表達式的左操作數和右操作數上的特殊方法。首先，Python 會檢查左操作數的__add__方法，之後檢查右操作數的__radd__方法。如果二者之一被發現，這個方法會以另一個操作數的值作為參數調用。

在 Python 中求解含有任何類型的運算符的表達值具有相似的協議，這包括切片符號和布爾運算符。Python 文檔列出了完整的運算符的方法名稱。Dive into Python 3 的特殊方法名稱一章描述了許多用於 Python 解釋器的細節。

2.7.3 泛用函數

我們的複數實現創建了兩種數據類型，它們對於add_complex和mul_complex函數能夠互相轉換。現在我們要看看如何使用相同的概念，不僅僅定義不同表示上的泛用操作，也能用來定義不同種類、並且不共享通用結構的參數上的泛用操作。

我們到目前為止已定義的操作將不同的數據類型獨立對待。所以，存在用於加法的獨立的包，比如兩個有理數或者兩個複數。我們沒有考慮到的是，定義類型界限之間的操作很有意義，比如將複數與有理數相加。我們經歷了巨大的痛苦，引入了程序中各個部分的界限，便於讓它們可被獨立開發和理解。

我們希望以某種精確控制的方式引入跨類型的操作。便於在不嚴重違反抽象界限的情況下支持它們。在我們希望的結果之間可能有些矛盾：我們希望能夠將有理數與複數相加，也希望能夠使用泛用的add函數，正確處理所有數值類型。同時，我們希望隔離複數和有理數的細節，來維持程序的模塊化。

讓我們使用 Python 內建的對象系統重新編寫有理數的實現。像之前一樣，我們在較低層級將有理數儲存為分子和分母。

>>> from fractions import gcd
>>> class Rational(object):
        def __init__(self, numer, denom):
            g = gcd(numer, denom)
            self.numer = numer // g
            self.denom = denom // g
        def __repr__(self):
            return 'Rational({0}, {1})'.format(self.numer, self.denom)

這個新的實現中的有理數的加法和乘法和之前類似。

>>> def add_rational(x, y):
        nx, dx = x.numer, x.denom
        ny, dy = y.numer, y.denom
        return Rational(nx * dy + ny * dx, dx * dy)
>>> def mul_rational(x, y):
        return Rational(x.numer * y.numer, x.denom * y.denom)

**類型分發。**一種處理跨類型操作的方式是為每種可能的類型組合設計不同的函數，操作可用於這種類型。例如，我們可以擴展我們的複數實現，使其提供函數用於將複數與有理數相加。我們可以使用叫做類型分發的機制更通用地提供這個功能。

類型分發的概念是，編寫一個函數，首先檢測接受到的參數類型，之後執行適用於這種類型的代碼。Python 中，對象類型可以使用內建的type函數來檢測。

>>> def iscomplex(z):
        return type(z) in (ComplexRI, ComplexMA)
>>> def isrational(z):
        return type(z) == Rational

這裡，我們依賴一個事實，每個對象都知道自己的類型，並且我們可以使用Python 的type函數來獲取類型。即使type函數不可用，我們也能根據Rational，ComplexRI和ComplexMA來實現iscomplex和isrational。

現在考慮下面的add實現，它顯式檢查了兩個參數的類型。我們不會在這個例子中顯式使用 Python 的特殊方法（例如__add__）。

>>> def add_complex_and_rational(z, r):
            return ComplexRI(z.real + r.numer/r.denom, z.imag)
>>> def add(z1, z2):
        """Add z1 and z2, which may be complex or rational."""
        if iscomplex(z1) and iscomplex(z2):
            return add_complex(z1, z2)
        elif iscomplex(z1) and isrational(z2):
            return add_complex_and_rational(z1, z2)
        elif isrational(z1) and iscomplex(z2):
            return add_complex_and_rational(z2, z1)
        else:
            return add_rational(z1, z2)

這個簡單的類型分發方式並不是遞增的，它使用了大量的條件語句。如果另一個數值類型包含在程序中，我們需要使用新的語句重新實現add。

我們可以創建更靈活的add實現，通過以字典實現類型分發。要想擴展add的靈活性，第一步是為我們的類創建一個tag集合，抽離兩個複數集合的實現。

>>> def type_tag(x):
        return type_tag.tags[type(x)]
>>> type_tag.tags = {ComplexRI: 'com', ComplexMA: 'com', Rational: 'rat'}

下面，我們使用這些類型標籤來索引字典，字典中儲存了數值加法的不同方式。字典的鍵是類型標籤的元素，值是類型特定的加法函數。

>>> def add(z1, z2):
        types = (type_tag(z1), type_tag(z2))
        return add.implementations[types](z1, z2)

add函數的定義本身沒有任何功能；它完全地依賴於一個叫做add.implementations的字典去實現泛用加法。我們可以構建如下的字典。

>>> add.implementations = {}
>>> add.implementations[('com', 'com')] = add_complex
>>> add.implementations[('com', 'rat')] = add_complex_and_rational
>>> add.implementations[('rat', 'com')] = lambda x, y: add_complex_and_rational(y, x)
>>> add.implementations[('rat', 'rat')] = add_rational

這個基於字典的分發方式是遞增的，因為add.implementations和type_tag.tags總是可以擴展。任何新的數值類型可以將自己“安裝”到現存的系統中，通過向這些字典添加新的條目。

當我們向系統引入一些複雜性時，我們現在擁有了泛用、可擴展的add函數，可以處理混合類型。

>>> add(ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> add(Rational(5, 3), Rational(1, 2))
Rational(13, 6)

**數據導向編程。**我們基於字典的add實現並不是特定於加法的；它不包含任何加法的直接邏輯。它只實現了加法操作，因為我們碰巧將implementations字典和函數放到一起來執行加法。

更通用的泛用算數操作版本會將任意運算符作用於任意類型，並且使用字典來儲存多種組合的實現。這個完全泛用的實現方法的方式叫做數據導向編程。在我們這裡，我們可以實現泛用加法和乘法，而不帶任何重複的邏輯。

>>> def apply(operator_name, x, y):
        tags = (type_tag(x), type_tag(y))
        key = (operator_name, tags)
        return apply.implementations[key](x, y)

在泛用的apply函數中，鍵由操作數的名稱（例如add），和參數類型標籤的元組構造。我們下面添加了對複數和有理數的乘法支持。

>>> def mul_complex_and_rational(z, r):
        return ComplexMA(z.magnitude * r.numer / r.denom, z.angle)
>>> mul_rational_and_complex = lambda r, z: mul_complex_and_rational(z, r)
>>> apply.implementations = {('mul', ('com', 'com')): mul_complex,
                             ('mul', ('com', 'rat')): mul_complex_and_rational,
                             ('mul', ('rat', 'com')): mul_rational_and_complex,
                             ('mul', ('rat', 'rat')): mul_rational}

我們也可以使用字典的update方法，從add中將加法實現添加到apply。

>>> adders = add.implementations.items()
>>> apply.implementations.update({('add', tags):fn for (tags, fn) in adders})

既然已經在單一的表中支持了 8 種不同的實現，我們可以用它來更通用地操作有理數和複數。

>>> apply('add', ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> apply('mul', Rational(1, 2), ComplexMA(10, 1))
ComplexMA(5.0, 1)

這個數據導向的方式管理了跨類型運算符的複雜性，但是十分麻煩。使用這個一個系統，引入新類型的開銷不僅僅是為類型編寫方法，還有實現跨類型操作的函數的構造和安裝。這個負擔比起定義類型本身的操作需要更多代碼。

當類型分發機制和數據導向編程的確能創造泛用函數的遞增實現時，它們就不能有效隔離實現的細節。獨立數值類型的實現者需要在編程跨類型操作時考慮其他類型。組合有理數和複數嚴格上並不是每種類型的範圍。在類型中制定一致的責任分工政策，在帶有多種類型和跨類型操作的系統設計中是大勢所趨。

**強制轉換。**在完全不相關的類型執行完全不相關的操作的一般情況中，實現顯式的跨類型操作，儘管可能非常麻煩，是人們所希望的最佳方案。幸運的是，我們有時可以通過利用類型系統中隱藏的額外結構來做得更好。不同的數據類通常並不是完全獨立的，可能有一些方式，一個類型的對象通過它會被看做另一種類型的對象。這個過程叫做強制轉換。例如，如果我們被要求將一個有理數和一個複數通過算數來組合，我們可以將有理數看做虛部為零的複數。通過這樣做，我們將問題轉換為兩個複數組合的問題，這可以通過add_complex和mul_complex由經典的方法處理。

通常，我們可以通過設計強制轉換函數來實現這個想法。強制轉換函數將一個類型的對象轉換為另一個類型的等價對象。這裡是一個典型的強制轉換函數，它將有理數轉換為虛部為零的複數。

>>> def rational_to_complex(x):
        return ComplexRI(x.numer/x.denom, 0)

現在，我們可以定義強制轉換函數的字典。這個字典可以在更多的數值類型引入時擴展。

>>> coercions = {('rat', 'com'): rational_to_complex}

任意類型的數據對象不可能轉換為每個其它類型的對象。例如，沒有辦法將任意的複數強制轉換為有理數，所以在coercions字典中應該沒有這種轉換的實現。

使用coercions字典，我們可以編寫叫做coerce_apply的函數，它試圖將參數強制轉換為相同類型的值，之後僅僅調用運算符。coerce_apply 的實現字典不包含任何跨類型運算符的實現。

>>> def coerce_apply(operator_name, x, y):
        tx, ty = type_tag(x), type_tag(y)
        if tx != ty:
            if (tx, ty) in coercions:
                tx, x = ty, coercions[(tx, ty)](x)
            elif (ty, tx) in coercions:
                ty, y = tx, coercions[(ty, tx)](y)
            else:
                return 'No coercion possible.'
        key = (operator_name, tx)
        return coerce_apply.implementations[key](x, y)

coerce_apply的implementations僅僅需要一個類型標籤，因為它們假設兩個值都共享相同的類型標籤。所以，我們僅僅需要四個實現來支持複數和有理數上的泛用算數。

>>> coerce_apply.implementations = {('mul', 'com'): mul_complex,
                                    ('mul', 'rat'): mul_rational,
                                    ('add', 'com'): add_complex,
                                    ('add', 'rat'): add_rational}

就地使用這些實現，coerce_apply 可以代替apply。

>>> coerce_apply('add', ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> coerce_apply('mul', Rational(1, 2), ComplexMA(10, 1))
ComplexMA(5.0, 1.0)

這個強制轉換的模式比起顯式定義跨類型運算符的方式具有優勢。雖然我們仍然需要編程強制轉換函數來關聯類型，我們僅僅需要為每對類型編寫一個函數，而不是為每個類型組合和每個泛用方法編寫不同的函數。我們所期望的是，類型間的合理轉換僅僅依賴於類型本身，而不是要調用的特定操作。

強制轉換的擴展會帶來進一步的優勢。一些更復雜的強制轉換模式並不僅僅試圖將一個類型強制轉換為另一個，而是將兩個不同類型強制轉換為第三個。想一想菱形和長方形：每個都不是另一個的特例，但是兩個都可以看做平行四邊形。另一個強制轉換的擴展是迭代的強制轉換，其中一個數據類型通過媒介類型被強制轉換為另一種。一個整數可以轉換為一個實數，通過首先轉換為有理數，接著將有理數轉換為實數。這種方式的鏈式強制轉換降低了程序所需的轉換函數總數。

雖然它具有優勢，強制轉換也有潛在的缺陷。例如，強制轉換函數在調用時會丟失信息。在我們的例子中，有理數是精確表示，但是當它們轉換為複數時會變得近似。

一些編程語言擁有內建的強制轉換函數。實際上，Python 的早期版本擁有對象上的__coerce__特殊方法。最後，內建強制轉換系統的複雜性並不能支持它的使用，所以被移除了。反之，特定的操作按需強制轉換它們的參數。運算符被實現為用戶定義類上的特殊方法，比如__add__和__mul__。這完全取決於你，取決於用戶來決定是否使用類型分發，數據導向編程，消息傳遞，或者強制轉換來在你的程序中實現泛用函數。

第三章 計算機程序的構造和解釋

3.1 引言

來源：3.1 Introduction

譯者：飛龍

協議：CC BY-NC-SA 4.0

第一章和第二章描述了編程的兩個基本元素：數據和函數之間的緊密聯繫。我們看到了高階函數如何將函數當做數據操作。我們也看到了數據可以使用消息傳遞和對象系統綁定行為。我們已經學到了組織大型程序的技巧，例如函數抽象，數據抽象，類的繼承，以及泛用函數。這些核心概念構成了堅實的基礎，來構建模塊化，可維護和可擴展的程序。

這一章專注於編程的第三個基本元素：程序自身。Python 程序只是文本的集合。只有通過解釋過程，我們才可以基於文本執行任何有意義的計算。類似 Python 的編程語言很實用，因為我們可以定義解釋器，它是一個執行 Python 求值和執行過程的程序。把它看做編程中最基本的概念並不誇張。解釋器只是另一個程序，它確定編程語言中表達式的意義。

接受這一概念，需要改變我們自己作為程序員的印象。我們需要將自己看做語言的設計者，而不只是由他人設計的語言用戶。

3.1.1 編程語言

實際上，我們可以將許多程序看做一些語言的解釋器。例如，上一章的約束傳播器擁有自己的原語和組合方式。約束語言是十分專用的：它提供了一種聲明式的方式來描述數學關係的特定種類，而不是一種用於描述計算的完全通用的語言。雖然我們已經設計了某種語言，這章的材料會極大擴展我們可解釋的語言範圍。

編程語言在語法結構、特性和應用領域上差別很大。在通用編程語言中，函數定義和函數調用的結構無處不在。另一方法，存在不包含對象系統、高階函數或類似while和for語句的控制結構的強大的編程語言。為了展示語言可以有多麼不同，我們會引入Logo作為強大並且具有表現力的編程語言的例子，它包含非常少的高級特性。

這一章中，我們會學習解釋器的設計，以及在執行程序時，它們所創建的計算過程。為通用語言設計解釋器的想法可能令人畏懼。畢竟，解釋器是執行任何可能計算的程序，取決於它們的輸入。但是，典型的解釋器擁有簡潔的通用結構：兩個可變的遞歸函數，第一個求解環境中的表達式，第二個在參數上調用函數。

這些函數都是遞歸的，因為它們互相定義：調用函數需要求出函數體的表達式，而求出表達式可能涉及到調用一個或多個函數。這一章接下來的兩節專注於遞歸函數和數據結構，它們是理解解釋器設計的基礎。這一章的結尾專注於兩個新的編程語言，以及為其實現解釋器的任務。

3.2 函數和所生成的過程

來源：3.2 Functions and the Processes They Generate

譯者：飛龍

協議：CC BY-NC-SA 4.0

函數是計算過程的局部演化模式。它規定了過程的每個階段如何構建在之前的階段之上。我們希望能夠創建有關過程整體行為的語句，而過程的局部演化由一個或多個函數指定。這種分析通常非常困難，但是我們至少可以試圖描述一些典型的過程演化模式。

在這一章中，我們會檢測一些用於簡單函數所生成過程的通用“模型”。我們也會研究這些過程消耗重要的計算資源，例如時間和空間的比例。

3.2.1 遞歸函數

如果函數的函數體直接或者間接自己調用自己，那麼這個函數是遞歸的。也就是說，遞歸函數的執行過程可能需要再次調用這個函數。Python 中的遞歸函數不需要任何特殊的語法，但是它們的確需要一些注意來正確定義。

作為遞歸函數的介紹，我們以將英文單詞轉換為它的 Pig Latin 等價形式開始。Pig Latin 是一種隱語：對英文單詞使用一種簡單、確定的轉換來掩蓋單詞的含義。Thomas Jefferson 據推測是先行者。英文單詞的 Pig Latin 等價形式將輔音前綴（可能為空）從開頭移動到末尾，並且添加-ay元音。所以，pun會變成unpay，stout會變成outstay，all會變成allay。

>>> def pig_latin(w):
        """Return the Pig Latin equivalent of English word w."""
        if starts_with_a_vowel(w):
            return w + 'ay'
        return pig_latin(w[1:] + w[0])
>>> def starts_with_a_vowel(w):
        """Return whether w begins with a vowel."""
        return w[0].lower() in 'aeiou'

這個定義背後的想法是，一個以輔音開頭的字符串的 Pig Latin 變體和另一個字符串的 Pig Latin 變體相同：它通過將第一個字母移到末尾來創建。於是，sending的 Pig Latin 變體就和endings的變體（endingsay）相同。smother的 Pig Latin 變體和mothers的變體（othersmay）相同。而且，將輔音從開頭移動到末尾會產生帶有更少輔音前綴的更簡單的問題。在sending的例子中，將s移動到末尾會產生以元音開頭的單詞，我們的任務就完成了。

即使pig_latin函數在它的函數體中調用，pig_latin的定義是完整且正確的。

>>> pig_latin('pun')
'unpay'

能夠基於函數自身來定義函數的想法可能十分令人混亂：“循環”定義如何有意義，這看起來不是很清楚，更不用說讓計算機來執行定義好的過程。但是，我們能夠準確理解遞歸函數如何使用我們的計算環境模型來成功調用。環境的圖示和描述pig_latin('pun')求值的表達式樹展示在下面：

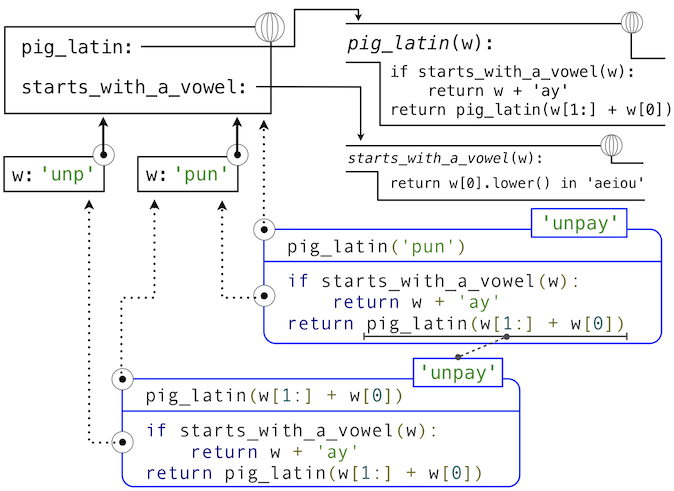
Python 求值過程的步驟產生如下結果：

1. pig_latin 的def語句 被執行，其中：
   1. 使用函數體創建新的pig_latin函數對象，並且
   2. 將名稱pig_latin在當前（全局）幀中綁定到這個函數上。
2. starts_with_a_vowel 的def語句類似地執行。
3. 求出pig_latin('pun')的調用表達式，通過
   1. 求出運算符和操作數子表達式，通過
      1. 查找綁定到pig_latin函數的pig_latin名稱
      2. 對字符串對象'pun'求出操作數字符串字面值
   2. 在參數'pun'上調用pig_latin函數，通過
      1. 添加擴展自全局幀的局部幀
      2. 將形參w綁定到當前幀的實參'pun'上。
      3. 在以當前幀起始的環境中執行pig_latin的函數體
         1. 最開始的條件語句沒有效果，因為頭部表達式求值為False
         2. 求出最後的返回表達式pig_latin(w[1:] + w[0])，通過
            1. 查找綁定到pig_latin函數的pig_latin名稱
            2. 對字符串對象'pun'求出操作數表達式
            3. 在參數'unp'上調用pig_latin，它會從pig_latin函數體中的條件語句組返回預期結果。

就像這個例子所展示的那樣，雖然遞歸函數具有循環特徵，他仍舊正確調用。pig_latin函數調用了兩次，但是每次都帶有不同的參數。雖然第二個調用來自pig_latin自己的函數體，但由名稱查找函數會成功，因為名稱pig_latin在它的函數體執行前的環境中綁定。

這個例子也展示了 Python 的遞歸函數的求值過程如何與遞歸函數交互，來產生帶有許多嵌套步驟的複雜計算過程，即使函數定義本身可能包含非常少的代碼行數。

3.2.2 剖析遞歸函數

許多遞歸函數的函數體中都存在通用模式。函數體以基本條件開始，它是一個條件語句，為需要處理的最簡單的輸入定義函數行為。在pig_latin的例子中，基本條件對任何以元音開頭的單詞成立。這個時候，只需要返回末尾附加ay的參數。一些遞歸函數會有多重基本條件。

基本條件之後是一個或多個遞歸調用。遞歸調用有特定的特徵：它們必須簡化原始問題。在pig_latin的例子中，w中最開始輔音越多，就需要越多的處理工作。在遞歸調用pig_latin(w[1:] + w[0])中，我們在一個具有更少初始輔音的單詞上調用pig_latin -- 這就是更簡化的問題。每個成功的pig_latin調用都會更加簡化，直到滿足了基本條件：一個沒有初始輔音的單詞。

遞歸調用通過逐步簡化問題來表達計算。與我們在過去使用過的迭代方式相比，它們通常以不同方式來解決問題。考慮用於計算n的階乘的函數fact，其中fact(4)計算了4! = 4·3·2·1 = 24。

使用while語句的自然實現會通過將每個截至n的正數相乘來求出結果。

>>> def fact_iter(n):
        total, k = 1, 1
        while k <= n:
            total, k = total * k, k + 1
        return total
>>> fact_iter(4)
24

另一方面，階乘的遞歸實現可以以fact(n-1)（一個更簡單的問題）來表示fact(n)。遞歸的基本條件是問題的最簡形式：fact(1)是1。

>>> def fact(n):
        if n == 1:
            return 1
        return n * fact(n-1)
>>> fact(4)
24

函數的正確性可以輕易通過階乘函數的標準數學定義來驗證。

(n − 1)! = (n − 1)·(n − 2)· ... · 1
n！ = n·(n − 1)·(n − 2)· ... · 1
n! = n·(n − 1)!  

這兩個階乘函數在概念上不同。迭代的函數通過將每個式子，從基本條件1到最終的總數逐步相乘來構造結果。另一方面，遞歸函數直接從最終的式子n和簡化的問題fact(n-1)構造結果。

將fact函數應用於更簡單的問題實例，來展開遞歸的同時，結果最終由基本條件構建。下面的圖示展示了遞歸如何向fact傳入1而終止，以及每個調用的結果如何依賴於下一個調用，直到滿足了基本條件。

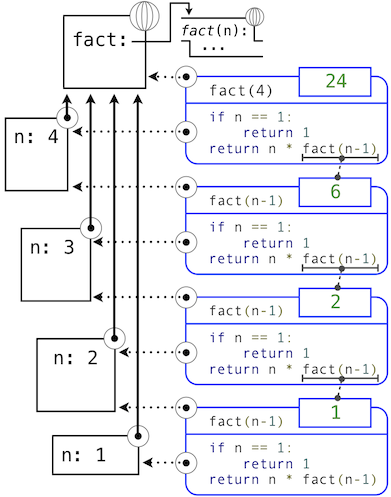
雖然我們可以使用我們的計算模型展開遞歸，通常把遞歸調用看做函數抽象更清晰一些。也就是說，我們不應該關心fact(n-1)如何在fact的函數體中實現；我們只需要相信它計算了n-1的階乘。將遞歸調用看做函數抽象叫做遞歸的“信仰飛躍”（leap of faith）。我們以函數自身來定義函數，但是僅僅相信更簡單的情況在驗證函數正確性時會正常工作。這個例子中我們相信，fact(n-1)會正確計算(n-1)!；我們只需要檢查，如果滿足假設n!是否正確計算。這樣，遞歸函數正確性的驗證就變成了一種歸納證明。

函數fact_iter和fact也不一樣，因為前者必須引入兩個額外的名稱，total和k，它們在遞歸實現中並不需要。通常，迭代函數必須維護一些局部狀態，它們會在計算過程中改變。在任何迭代的時間點上，狀態刻畫了已完成的結果，以及未完成的工作總量。例如，當k為3且total為2時，就還剩下兩個式子沒有處理，3和4。另一方面，fact由單一參數n來刻畫。計算的狀態完全包含在表達式樹的結果中，它的返回值起到total的作用，並且在不同的幀中將n綁定到不同的值上，而不是顯式跟蹤k。

遞歸函數可以更加依賴於解釋器本身，通過將計算狀態儲存為表達式樹和環境的一部分，而不是顯式使用局部幀中的名稱。出於這個原因，遞歸函數通常易於定義，因為我們不需要試著弄清必須在迭代中維護的局部狀態。另一方面，學會弄清由遞歸函數實現的計算過程，需要一些練習。

3.2.3 樹形遞歸

另一個遞歸的普遍模式叫做樹形遞歸。例如，考慮斐波那契序列的計算，其中每個數值都是前兩個的和。

>>> def fib(n):
        if n == 1:
            return 0
        if n == 2:
            return 1
        return fib(n-2) + fib(n-1)
>>> fib(6)
5

這個遞歸定義和我們之前的嘗試有很大關係：它準確反映了斐波那契數的相似定義。考慮求出fib(6)所產生的計算模式，它展示在下面。為了計算fib(6)，我們需要計算fib(5)和fib(4)。為了計算fib(5)，我們需要計算fib(4)和fib(3)。通常，這個演化過程看起來像一棵樹（下面的圖並不是完整的表達式樹，而是簡化的過程描述；一個完整的表達式樹也擁有同樣的結構）。在遍歷這棵樹的過程中，每個藍點都表示斐波那契數的已完成計算。

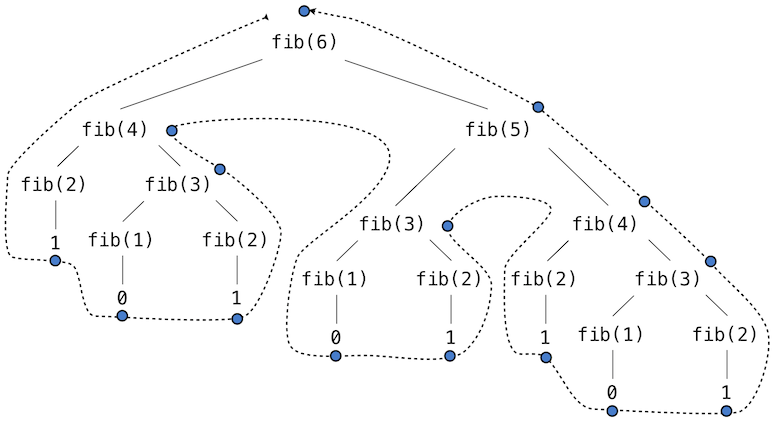
調用自身多次的函數叫做樹形遞歸。以樹形遞歸為原型編寫的函數十分有用，但是用於計算斐波那契數則非常糟糕，因為它做了很多重複的計算。要注意整個fib(4)的計算是重複的，它幾乎是一半的工作量。實際上，不難得出函數用於計算fib(1)和fib(2)（通常是樹中的葉子數量）的時間是fib(n+1)。為了弄清楚這有多糟糕，我們可以證明fib(n)的值隨著n以指數方式增長。所以，這個過程的步驟數量隨輸入以指數方式增長。

我們已經見過斐波那契數的迭代實現，出於便利在這裡貼出來：

>>> def fib_iter(n):
        prev, curr = 1, 0  # curr is the first Fibonacci number.
        for _ in range(n-1):
             prev, curr = curr, prev + curr
        return curr

這裡我們必須維護的狀態由當前值和上一個斐波那契數組成。for語句也顯式跟蹤了迭代數量。這個定義並沒有像遞歸方式那樣清晰反映斐波那契數的數學定義。但是，迭代實現中所需的計算總數只是線性，而不是指數於n的。甚至對於n的較小值，這個差異都非常大。

然而我們不應該從這個差異總結出，樹形遞歸的過程是沒有用的。當我們考慮層次數據結構，而不是數值上的操作時，我們發現樹形遞歸是自然而強大的工具。而且，樹形過程可以變得更高效。

**記憶。**用於提升重複計算的遞歸函數效率的機制叫做記憶。記憶函數會為任何之前接受的參數儲存返回值。fib(4)的第二次調用不會執行與第一次同樣的複雜過程，而是直接返回第一次調用的已儲存結果。

記憶函數可以自然表達為高階函數，也可以用作裝飾器。下面的定義為之前的已計算結果創建緩存，由被計算的參數索引。在這個實現中，這個字典的使用需要記憶函數的參數是不可變的。

>>> def memo(f):
        """Return a memoized version of single-argument function f."""
        cache = {}
        def memoized(n):
            if n not in cache:
                cache[n] = f(n)
            return cache[n]
        return memoized
>>> fib = memo(fib)
>>> fib(40)
63245986

由記憶函數節省的所需的計算時間總數在這個例子中是巨大的。被記憶的遞歸函數fib和迭代函數fib_iter都只需要線性於輸入n的時間總數。為了計算fib(40)，fib的函數體只執行 40 次，而不是無記憶遞歸中的 102,334,155 次。

**空間。**為了理解函數所需的空間，我們必須在我們的計算模型中規定內存如何使用，保留和回收。在求解表達式過程中，我們必須保留所有活動環境和所有這些環境引用的值和幀。如果環境為表達式樹當前分支中的一些表達式提供求值上下文，那麼它就是活動環境。

例如，當求值fib時，解釋器按序計算之前的每個值，遍歷樹形結構。為了這樣做，它只需要在計算的任何時間點，跟蹤樹中在當前節點之前的那些節點。用於求出剩餘節點的內存可以被回收，因為它不會影響未來的計算。通常，樹形遞歸所需空間與樹的深度成正比。

下面的圖示描述了由求解fib(3)生成的表達式樹。在求解fib最初調用的返回表達式的過程中，fib(n-2)被求值，產生值0。一旦這個值計算出來，對應的環境幀（標為灰色）就不再需要了：它並不是活動環境的一部分。所以，一個設計良好的解釋器會回收用於儲存這個幀的內存。另一方面，如果解釋器當前正在求解fib(n-1)，那麼由這次fib調用（其中n為2）創建的環境是活動的。與之對應，最開始在3上調用fib所創建的環境也是活動的，因為這個值還沒有成功計算出來。

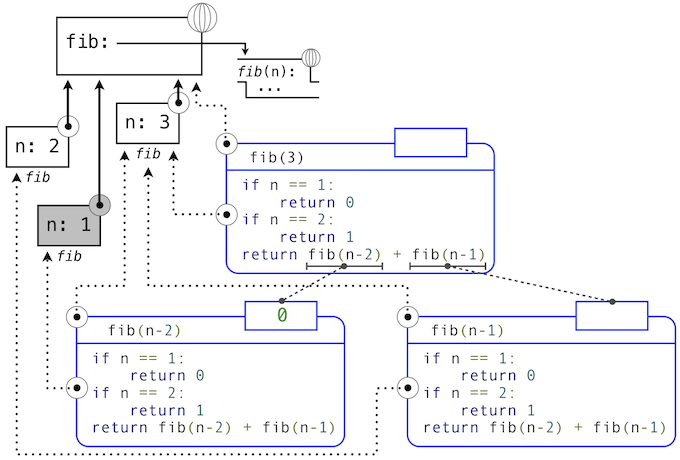
在memo的例子中，只要一些名稱綁定到了活動環境中的某個函數上，關聯到所返回函數（它包含cache）的環境必須保留。cache字典中的條目數量隨傳遞給fib的唯一參數數量線性增長，它的規模線性於輸入。另一方面，迭代實現只需要兩個數值來在計算過程中跟蹤：prev和curr，所以是常數大小。

我們使用記憶函數的例子展示了編程中的通用模式，即通常可以通過增加所用空間來減少計算時間，反之亦然。

3.2.4 示例：找零

考慮下面這個問題：如果給你半美元、四分之一美元、十美分、五美分和一美分，一美元有多少種找零的方式？更通常來說，我們能不能編寫一個函數，使用一系列貨幣的面額，計算有多少種方式為給定的金額總數找零？

這個問題可以用遞歸函數簡單解決。假設我們認為可用的硬幣類型以某種順序排列，假設從大到小排列。

使用n種硬幣找零的方式為：

1. 使用所有除了第一種之外的硬幣為a找零的方式，以及
2. 使用n種硬幣為更小的金額a - d找零的方式，其中d是第一種硬幣的面額。

為了弄清楚為什麼這是正確的，可以看出，找零方式可以分為兩組，不使用第一種硬幣的方式，和使用它們的方式。所以，找零方式的總數等於不使用第一種硬幣為該金額找零的方式數量，加上使用第一種硬幣至少一次的方式數量。而後者的數量等於在使用第一種硬幣之後，為剩餘的金額找零的方式數量。

因此，我們可以遞歸將給定金額的找零問題，歸約為使用更少種類的硬幣為更小的金額找零的問題。仔細考慮這個歸約原則，並且說服自己，如果我們規定了下列基本條件，我們就可以使用它來描述算法：

1. 如果a正好是零，那麼有一種找零方式。
2. 如果a小於零，那麼有零種找零方式。
3. 如果n小於零，那麼有零種找零方式。

我們可以輕易將這個描述翻譯成遞歸函數：

>>> def count_change(a, kinds=(50, 25, 10, 5, 1)):
        """Return the number of ways to change amount a using coin kinds."""
        if a == 0:
            return 1
        if a < 0 or len(kinds) == 0:
            return 0
        d = kinds[0]
        return count_change(a, kinds[1:]) + count_change(a - d, kinds)
>>> count_change(100)
292

count_change函數生成樹形遞歸過程，和fib的首個實現一樣，它是重複的。它會花費很長時間來計算出292，除非我們記憶這個函數。另一方面，設計迭代算法來計算出結果的方式並不是那麼明顯，我們將它留做一個挑戰。

3.2.5 增長度

前面的例子表明，不同過程在花費的時間和空間計算資源上有顯著差異。我們用於描述這個差異的便捷方式，就是使用增長度的概念，來獲得當輸入變得更大時，過程所需資源的大致度量。

令n為度量問題規模的參數，R(n)為處理規模為n的問題的過程所需的資源總數。在我們前面的例子中，我們將n看做給定函數所要計算出的數值。但是還有其他可能。例如，如果我們的目標是計算某個數值的平方根近似值，我們會將n看做所需的有效位數的數量。通常，有一些問題相關的特性可用於分析給定的過程。與之相似，R(n)可用於度量所用的內存總數，所執行的基本的機器操作數量，以及其它。在一次只執行固定數量操作的計算中，用於求解表達式的所需時間，與求值過程中執行的基本機器操作數量成正比。

我們說，R(n)具有Θ(f(n))的增長度，寫作R(n)=Θ(f(n))（讀作“theta f(n)”），如果存在獨立於n的常數k1和k2，那麼對於任何足夠大的n值：

k1·f(n) <= R(n) <= k2·f(n)

也就是說，對於較大的n，R(n)的值夾在兩個具有f(n)規模的值之間：

• 下界k1·f(n)，以及
• 上界k2·f(n)。

例如，計算n!所需的步驟數量與n成正比，所以這個過程的所需步驟以Θ(n)增長。我們也看到了，遞歸實現fact的所需空間以Θ(n)增長。與之相反，迭代實現fact_iter 花費相似的步驟數量，但是所需的空間保持不變。這裡，我們說這個空間以Θ(1)增長。

我們的樹形遞歸的斐波那契數計算函數fib 的步驟數量，隨輸入n指數增長。尤其是，我們可以發現，第 n 個斐波那契數是距離φ^(n-2)/√5的最近整數，其中φ是黃金比例：

φ = (1 + √5)/2 ≈ 1.6180

我們也表示，步驟數量隨返回值增長而增長，所以樹形遞歸過程需要Θ(φ^n)的步驟，它的一個隨n指數增長的函數。

增長度只提供了過程行為的大致描述。例如，需要n^2個步驟的過程和需要1000·n^2個步驟的過程，以及需要3·n^2+10·n+17個步驟的過程都擁有Θ(n^2)的增長度。在特定的情況下，增長度的分析過於粗略，不能在函數的兩個可能實現中做出判斷。

但是，增長度提供了實用的方法，來表示在改變問題規模的時候，我們應如何預期過程行為的改變。對於Θ(n)（線性）的過程，使規模加倍只會使所需的資源總數加倍。對於指數的過程，每一點問題規模的增長都會使所用資源以固定因數翻倍。接下來的例子展示了一個增長度為對數的算法，所以使問題規模加倍，只會使所需資源以固定總數增加。

3.2.6 示例：求冪

考慮對給定數值求冪的問題。我們希望有一個函數，它接受底數b和正整數指數n作為參數，並計算出b^n。一種方式就是通過遞歸定義：

b^n = b·b^(n-1)
b^0 = 1

這可以翻譯成遞歸函數：

>>> def exp(b, n):
        if n == 0:
            return 1
        return b * exp(b, n-1)

這是個線性的遞歸過程，需要Θ(n)的步驟和空間。就像階乘那樣，我們可以編寫等價的線性迭代形式，它需要相似的步驟數量，但只需要固定的空間。

>>> def exp_iter(b, n):
        result = 1
        for _ in range(n):
            result = result * b
        return result

我們可以以更少的步驟求冪，通過逐次平方。例如，我們這樣計算b^8：

b·(b·(b·(b·(b·(b·(b·b))))))

我們可以使用三次乘法來計算它：

b^2 = b·b
b^4 = b^2·b^2
b^8 = b^4·b^4

這個方法對於 2 的冪的指數工作良好。我們也可以使用這個遞歸規則，在求冪中利用逐步平方的優點：

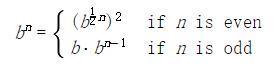
我們同樣可以將這個方式表達為遞歸函數：

>>> def square(x):
        return x*x
>>> def fast_exp(b, n):
        if n == 0:
            return 1
        if n % 2 == 0:
            return square(fast_exp(b, n//2))
        else:
            return b * fast_exp(b, n-1)
>>> fast_exp(2, 100)
1267650600228229401496703205376

fast_exp所生成的過程的空間和步驟數量隨n以對數方式增長。為了弄清楚它，可以看出，使用fast_exp計算b^2n比計算b^n只需要一步額外的乘法操作。於是，我們能夠計算的指數大小，在每次新的乘法操作時都會（近似）加倍。所以，計算n的指數所需乘法操作的數量，增長得像以2為底n的對數那樣慢。這個過程擁有Θ(log n)的增長度。Θ(log n)和Θ(n)之間的差異在n非常大時變得顯著。例如，n為1000時，fast_exp 僅僅需要14個乘法操作，而不是1000。

3.3 遞歸數據結構

來源：3.3 Recursive Data Structures

譯者：飛龍

協議：CC BY-NC-SA 4.0

在第二章中，我們引入了偶對的概念，作為一種將兩個對象結合為一個對象的機制。我們展示了偶對可以使用內建元素來實現。偶對的封閉性表明偶對的每個元素本身都可以為偶對。

這種封閉性允許我們實現遞歸列表的數據抽象，它是我們的第一種序列類型。遞歸列表可以使用遞歸函數最為自然地操作，就像它們的名稱和結構表示的那樣。在這一節中，我們會討論操作遞歸列表和其它遞歸結構的自定義的函數。

3.3.1 處理遞歸列表

遞歸列表結構將列表表示為首個元素和列表的剩餘部分的組合。我們之前使用函數實現了遞歸列表，但是現在我們可以使用類來重新實現。下面，長度（__len__）和元素選擇（__getitem__）被重寫來展示處理遞歸列表的典型模式。

>>> class Rlist(object):
        """A recursive list consisting of a first element and the rest."""
        class EmptyList(object):
            def __len__(self):
                return 0
        empty = EmptyList()
        def __init__(self, first, rest=empty):
            self.first = first
            self.rest = rest
        def __repr__(self):
            args = repr(self.first)
            if self.rest is not Rlist.empty:
                args += ', {0}'.format(repr(self.rest))
            return 'Rlist({0})'.format(args)
        def __len__(self):
            return 1 + len(self.rest)
        def __getitem__(self, i):
            if i == 0:
                return self.first
            return self.rest[i-1]

__len__和__getitem__的定義實際上是遞歸的，雖然不是那麼明顯。Python 內建函數len在自定義對象的參數上調用時會尋找叫做__len__的方法。與之類似，下標運算符會尋找叫做__getitem__的方法。於是，這些定義最後會調用對象自身。剩餘部分上的遞歸調用是遞歸列表處理的普遍模式。這個遞歸列表的類定義與 Python 的內建序列和打印操作能夠合理交互。

>>> s = Rlist(1, Rlist(2, Rlist(3)))
>>> s.rest
Rlist(2, Rlist(3))
>>> len(s)
3
>>> s[1]
2

創建新列表的操作能夠直接使用遞歸來表示。例如，我們可以定義extend_rlist函數，它接受兩個遞歸列表作為參數並將二者的元素組合到新列表中。

>>> def extend_rlist(s1, s2):
        if s1 is Rlist.empty:
            return s2
        return Rlist(s1.first, extend_rlist(s1.rest, s2))
>>> extend_rlist(s.rest, s)
Rlist(2, Rlist(3, Rlist(1, Rlist(2, Rlist(3)))))

與之類似，在遞歸列表上映射函數展示了相似的模式：

>>> def map_rlist(s, fn):
        if s is Rlist.empty:
            return s
        return Rlist(fn(s.first), map_rlist(s.rest, fn))
>>> map_rlist(s, square)
Rlist(1, Rlist(4, Rlist(9)))

過濾操作包括額外的條件語句，但是也擁有相似的遞歸結構。

>>> def filter_rlist(s, fn):
        if s is Rlist.empty:
            return s
        rest = filter_rlist(s.rest, fn)
        if fn(s.first):
            return Rlist(s.first, rest)
        return rest
>>> filter_rlist(s, lambda x: x % 2 == 1)
Rlist(1, Rlist(3))

列表操作的遞歸實現通常不需要局部賦值或者while語句。反之，遞歸列表可以作為函數調用的結果來拆分和構造。所以，它們擁有步驟數量和所需空間的線性增長度。

3.3.2 層次結構

層次結構產生於數據的封閉特性，例如，元組可以包含其它元組。考慮這個數值1到4的嵌套表示。

>>> ((1, 2), 3, 4)
((1, 2), 3, 4)

這個元組是個長度為 3 的序列，它的第一個元素也是一個元組。這個嵌套結構的盒子和指針的圖示表明，它可以看做擁有四個葉子的樹，每個葉子都是一個數值。

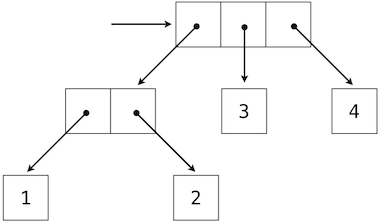
在樹中，每個子樹本身都是一棵樹。作為基本條件，任何本身不是元組的元素都是一個簡單的樹，沒有任何枝幹。也就是說，所有數值都是樹，就像在偶對(1, 2)和整個結構中那樣。

遞歸是用於處理樹形結構的自然工具，因為我們通常可以將樹的操作降至枝幹的操作，它會相應產生枝幹的枝幹的操作，以此類推，直到我們到達了樹的葉子。例如，我們可以實現count_leaves函數，它返回樹的葉子總數。

>>> t = ((1, 2), 3, 4)
>>> count_leaves(t)
4
>>> big_tree = ((t, t), 5)
>>> big_tree
((((1, 2), 3, 4), ((1, 2), 3, 4)), 5)
>>> count_leaves(big_tree)
9

正如map是用於處理序列的強大工具，映射和遞歸一起為樹的操作提供了強大而通用的計算形式。例如，我們可以使用高階遞歸函數map_tree 將樹的每個葉子平方，它的結構類似於count_leaves。

>>> def map_tree(tree, fn):
        if type(tree) != tuple:
            return fn(tree)
        return tuple(map_tree(branch, fn) for branch in tree)
>>> map_tree(big_tree, square)
((((1, 4), 9, 16), ((1, 4), 9, 16)), 25)

**內部值。**上面描述的樹只在葉子上存在值。另一個通用的樹形結構表示也在樹的內部節點上存在值。我們使用類來表示這種樹。

>>> class Tree(object):
        def __init__(self, entry, left=None, right=None):
            self.entry = entry
            self.left = left
            self.right = right
        def __repr__(self):
            args = repr(self.entry)
            if self.left or self.right:
                args += ', {0}, {1}'.format(repr(self.left), repr(self.right))
            return 'Tree({0})'.format(args)

例如，Tree類可以為fib的遞歸實現表示表達式樹中計算的值。fib函數用於計算斐波那契數。下面的函數fib_tree(n)返回Tree，它將第 n 個斐波那契樹作為entry，並將所有之前計算出來的斐波那契數存入它的枝幹中。

>>> def fib_tree(n):
        """Return a Tree that represents a recursive Fibonacci calculation."""
        if n == 1:
            return Tree(0)
        if n == 2:
            return Tree(1)
        left = fib_tree(n-2)
        right = fib_tree(n-1)
        return Tree(left.entry + right.entry, left, right)
>>> fib_tree(5)
Tree(3, Tree(1, Tree(0), Tree(1)), Tree(2, Tree(1), Tree(1, Tree(0), Tree(1))))

這個例子表明，表達式樹可以使用樹形結構編程表示。嵌套表達式和樹形數據結構的聯繫，在我們這一章稍後對解釋器設計的討論中起到核心作用。

3.3.3 集合

除了列表、元組和字典之外，Python 擁有第四種容器類型，叫做set。集合字面值遵循元素以花括號閉合的數學表示。重複的元素在構造中會移除。集合是無序容器，所以打印出來的順序可能和元素在集合字面值中的順序不同。

>>> s = {3, 2, 1, 4, 4}
>>> s
{1, 2, 3, 4}

Python 的集合支持多種操作，包括成員測試、長度計算和標準的交集並集操作。

>>> 3 in s
True
>>> len(s)
4
>>> s.union({1, 5})
{1, 2, 3, 4, 5}
>>> s.intersection({6, 5, 4, 3})
{3, 4}

除了union和intersection，Python 的集合還支持多種其它操作。斷言isdisjoint、issubset和issuperset提供了集合比較操作。集合是可變的，並且可以使用add、remove、discard和pop一次修改一個元素。額外的方法提供了多元素的修改，例如clear和update。Python 集合文檔十分詳細並足夠易懂。

**實現集合。**抽象上，集合是不同對象的容器，支持成員測試、交集、並集和附加操作。向集合添加元素會返回新的集合，它包含原始集合的所有元素，如果沒有重複的話，也包含新的元素。並集和交集運算返回出現在任意一個或兩個集合中的元素構成的集合。就像任何數據抽象那樣，我們可以隨意實現任何集合表示上的任何函數，只要它們提供這種行為。

在這章的剩餘部分，我們會考慮三個實現集合的不同方式，它們在表示上不同。我們會通過分析集合操作的增長度，刻畫這些不同表示的效率。我們也會使用這一章之前的Rlist和Tree類，它們可以編寫用於集合元素操作的簡單而優雅的遞歸解決方案。

**作為無序序列的集合。**一種集合的表示方式是看做沒有出現多於一次的元素的序列。空集由空序列來表示。成員測試會遞歸遍歷整個列表。

>>> def empty(s):
        return s is Rlist.empty
>>> def set_contains(s, v):
        """Return True if and only if set s contains v."""
        if empty(s):
            return False
        elif s.first == v:
            return True
        return set_contains(s.rest, v)
>>> s = Rlist(1, Rlist(2, Rlist(3)))
>>> set_contains(s, 2)
True
>>> set_contains(s, 5)
False

這個set_contains 的實現需要Θ(n)的時間來測試元素的成員性，其中n是集合s的大小。使用這個線性時間的成員測試函數，我們可以將元素添加到集合中，也是線性時間。

>>> def adjoin_set(s, v):
        """Return a set containing all elements of s and element v."""
        if set_contains(s, v):
            return s
        return Rlist(v, s)
>>> t = adjoin_set(s, 4)
>>> t
Rlist(4, Rlist(1, Rlist(2, Rlist(3))))

那麼問題來了，我們應該在設計表示時關注效率。計算兩個集合set1和set2的交集需要成員測試，但是這次每個set1的元素必須測試set2中的成員性，對於兩個大小為n的集合，這會產生步驟數量的平方增長度Θ(n^2)。

>>> def intersect_set(set1, set2):
        """Return a set containing all elements common to set1 and set2."""
        return filter_rlist(set1, lambda v: set_contains(set2, v))
>>> intersect_set(t, map_rlist(s, square))
Rlist(4, Rlist(1))

在計算兩個集合的並集時，我們必須小心避免兩次包含任意一個元素。union_set 函數也需要線性數量的成員測試，同樣會產生包含Θ(n^2)步驟的過程。

>>> def union_set(set1, set2):
        """Return a set containing all elements either in set1 or set2."""
        set1_not_set2 = filter_rlist(set1, lambda v: not set_contains(set2, v))
        return extend_rlist(set1_not_set2, set2)
>>> union_set(t, s)
Rlist(4, Rlist(1, Rlist(2, Rlist(3))))

**作為有序元組的集合。**一種加速我們的集合操作的方式是修改表示，使集合元素遞增排列。為了這樣做，我們需要一些比較兩個對象的方式，使我們能判斷哪個更大。Python 中，許多不同對象類型都可以使用<和>運算符比較，但是我們會專注於這個例子中的數值。我們會通過將元素遞增排列來表示數值集合。

有序的一個優點會在set_contains體現：在檢查對象是否存在時，我們不再需要掃描整個集合。如果我們到達了大於要尋找的元素的集合元素，我們就知道這個元素不在集合中：

>>> def set_contains(s, v):
        if empty(s) or s.first > v:
            return False
        elif s.first == v:
            return True
        return set_contains(s.rest, v)
>>> set_contains(s, 0)
False

這節省了多少步呢？最壞的情況中，我們所尋找的元素可能是集合中最大的元素，所以步驟數量和無序表示相同。另一方面，如果我們尋找許多不同大小的元素，我們可以預料到有時我們可以在列表開頭的位置停止搜索，其它情況下我們仍舊需要檢測整個列表。平均上我們應該需要檢測集合中一半的元素。所以，步驟數量的平均值應該是n/2。這還是Θ(n)的增長度，但是它確實會在平均上為我們節省之前實現的一半步驟數量。

我們可以通過重新實現intersect_set獲取更加可觀的速度提升。在無序表示中，這個操作需要Θ(n^2)的步驟，因為我們對set1的每個元素執行set2上的完整掃描。但是使用有序的實現，我們可以使用更加機智的方式。我們同時迭代兩個集合，跟蹤set1中的元素e1和set2中的元素e2。當e1和e2相等時，我們在交集中添加該元素。

但是，假設e1小於e2，由於e2比set2的剩餘元素更小，我們可以立即推斷出e1不會出現在set2剩餘部分的任何位置，因此也不會出現在交集中。所以，我們不再需要考慮e1，我們將它丟棄並來到set1的下一個元素。當e2 < e1時，我們可以使用相似的邏輯來步進set2中的元素。下面是這個函數：

>>> def intersect_set(set1, set2):
        if empty(set1) or empty(set2):
            return Rlist.empty
        e1, e2 = set1.first, set2.first
        if e1 == e2:
            return Rlist(e1, intersect_set(set1.rest, set2.rest))
        elif e1 < e2:
            return intersect_set(set1.rest, set2)
        elif e2 < e1:
            return intersect_set(set1, set2.rest)
>>> intersect_set(s, s.rest)
Rlist(2, Rlist(3))

為了估計這個過程所需的步驟數量，觀察每一步我們都縮小了至少集合的一個元素的大小。所以，所需的步驟數量最多為set1和set2的大小之和，而不是無序表示所需的大小之積。這是Θ(n)而不是Θ(n^2)的增長度 -- 即使集合大小適中，它也是一個相當可觀的加速。例如，兩個大小為100的集合的交集需要 200步，而不是無序表示的 10000 步。

表示為有序序列的集合的添加和並集操作也以線性時間計算。這些實現都留做練習。

**作為二叉樹的集合。**我們可以比有序列表表示做得更好，通過將幾個元素重新以樹的形式排列。我們使用之前引入的Tree類。樹根的entry持有集合的一個元素。left分支的元素包括所有小於樹根元素的元素。right分支的元素包括所有大於樹根元素的元素。下面的圖展示了一些樹，它們表示集合{1, 3, 5, 7, 9, 11}。相同的集合可能會以不同形式的樹來表示。有效表示所需的唯一條件就是所有left子樹的元素應該小於entry，並且所有right子樹的元素應該大於它。

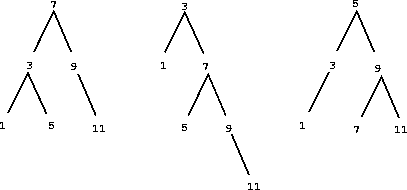
樹形表示的優點是：假設我們打算檢查v是否在集合中。我們通過將v於entry比較開始。如果v小於它，我們就知道了我們只需要搜索left子樹。如果v大於它，我們只需要搜索right子樹。現在如果樹是“平衡”的，每個這些子樹都約為整個的一半大小。所以，每一步中我們都可以將大小為n的樹的搜索問題降至搜索大小為n/2的子樹。由於樹的大小在每一步減半，我們應該預料到，用戶搜索樹的步驟以Θ(log n)增長。比起之前的表示，它的速度對於大型集合有可觀的提升。set_contains 函數利用了樹形集合的有序結構：

>>> def set_contains(s, v):
        if s is None:
            return False
        elif s.entry == v:
            return True
        elif s.entry < v:
            return set_contains(s.right, v)
        elif s.entry > v:
            return set_contains(s.left, v)

向集合添加元素與之類似，並且也需要Θ(log n)的增長度。為了添加值v，我們將v與entry比較，來決定v應該添加到right還是left分支，以及是否已經將v添加到了合適的分支上。我們將這個新構造的分支與原始的entry和其它分支組合。如果v等於entry，我們就可以返回這個節點。如果我們被要求將v添加到空的樹中，我們會生成一個Tree，它包含v作為entry，並且left和right都是空的分支。下面是這個函數：

>>> def adjoin_set(s, v):
        if s is None:
            return Tree(v)
        if s.entry == v:
            return s
        if s.entry < v:
            return Tree(s.entry, s.left, adjoin_set(s.right, v))
        if s.entry > v:
            return Tree(s.entry, adjoin_set(s.left, v), s.right)

>>> adjoin_set(adjoin_set(adjoin_set(None, 2), 3), 1)
Tree(2, Tree(1), Tree(3))

搜索該樹可以以對數步驟數量執行，我們這個敘述基於樹是“平衡”的假設。也就是說，樹的左子樹和右子樹都擁有相同數量的相應元素，使每個子樹含有母樹一半的元素。但是我們如何確定，我們構造的樹就是平衡的呢？即使我們以一顆平衡樹開始，使用adjoin_set添加元素也會產生不平衡的結果。由於新添加的元素位置取決於如何將元素與集合中的已有元素比較，我們可以預測，如果我們“隨機”添加元素到樹中，樹在平均上就會趨向於平衡。

但是這不是一個保證。例如，如果我們以空集開始，並向序列中添加 1 到 7，我們就會在最後得到很不平衡的樹，其中所有左子樹都是空的，所以它與簡單的有序列表相比並沒有什麼優勢。一種解決這個問題的方式是定義一種操作，它將任意的樹轉換為具有相同元素的平衡樹。我們可以在每個adjoin_set操作之後執行這個轉換來保證我們的集合是平衡的。

交集和並集操作可以在樹形集合上以線性時間執行，通過將它們轉換為有序的列表，並轉換回來。細節留做練習。

**Python 集合實現。**Python 內建的set類型並沒有使用上述任意一種表示。反之，Python 使用了一種實現，它的成員測試和添加操作是（近似）常量時間的，基於一種叫做哈希（散列）的機制，這是其它課程的話題。內建的 Python 集合不能包含可變的數據類型，例如列表、字典或者其它集合。為了能夠嵌套集合，Python 也提供了一種內建的不可變frozenset 類，除了可變操作和運算符之外，它擁有和set相同的方法。

3.4 異常

來源：3.4 Exceptions

譯者：飛龍

協議：CC BY-NC-SA 4.0

程序員必須總是留意程序中可能出現的錯誤。例子數不勝數：一個函數可能不會收到它預期的信息，必需的資源可能會丟失，或者網絡上的連接可能丟失。在設計系統時，程序員必須預料到可能產生的異常情況並且採取適當地措施來處理它們。

處理程序中的錯誤沒有單一的正確方式。為提供一些持久性服務而設計的程序，例如 Web 服務器 應該對錯誤健壯，將它們記錄到日誌中為之後考慮，而且在儘可能長的時間內繼續接受新的請求。另一方面，Python 解釋器通過立即終止以及打印錯誤信息來處理錯誤，便於程序員在錯誤發生時處理它。在任何情況下，程序員必須決定程序如何對異常條件做出反應。

異常是這一節的話題，它為程序的錯誤處理提供了通用的機制。產生異常是一種技巧，終止程序正常執行流，發射異常情況產生的信號，並直接返回到用於響應異常情況的程序的封閉部分。Python 解釋器每次在檢測到語句或表達式錯誤時拋出異常。用戶也可以使用raise或assert語句來拋出異常。

**拋出異常。**異常是一個對象實例，它的類直接或間接繼承自BaseException類。第一章引入的assert語句產生AssertionError類的異常。通常，異常實例可以使用raise語句來拋出。raise語句的通用形式在 Python 文檔中描述。raise的最常見的作用是構造異常實例並拋出它。

>>> raise Exception('An error occurred')
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
Exception: an error occurred

當異常產生時，當前代碼塊的語句不會繼續執行。除非異常被解決了（下面會描述），解釋器會直接返回到“讀取-求值-打印”交互式循環中，或者在 Python 以文件參數啟動的情況下會完全終止。此外，解釋器會打印棧回溯，它是結構化的文本塊，描述了執行分支中的一系列嵌套的活動函數，它們是異常產生的位置。在上面的例子中，文件名稱<stdin>表示異常由用戶在交互式會話中產生，而不是文件中的代碼。

**處理異常。**異常可以使用封閉的try語句來處理。try語句由多個子句組成，第一個子句以try開始，剩下的以except開始。

try:
    <try suite>
except <exception class> as <name>:
    <except suite>
...

當try語句執行時，<try suite>總是會立即執行。except子句組只在<try suite>執行過程中的異常產生時執行。每個except子句指定了需要處理的異常的特定類。例如，如果<exception class>是AssertionError，那麼任何繼承自AssertionError的類實例都會被處理，標識符<name> 綁定到所產生的異常對象上，但是這個綁定在<except suite>之外並不有效。

例如，我們可以使用try語句來處理異常，在異常發生時將x綁定為0。

>>> try:
        x = 1/0
    except ZeroDivisionError as e:
        print('handling a', type(e))
        x = 0
handling a <class 'ZeroDivisionError'>
>>> x
0

try語句能夠處理產生在函數體中的異常，函數在<try suite>中調用。當異常產生時，控制流會直接跳到最近的try語句的能夠處理該異常類型的<except suite>的主體中。

>>> def invert(x):
        result = 1/x  # Raises a ZeroDivisionError if x is 0
        print('Never printed if x is 0')
        return result
>>> def invert_safe(x):
        try:
            return invert(x)
        except ZeroDivisionError as e:
            return str(e)
>>> invert_safe(2)
Never printed if x is 0
0.5
>>> invert_safe(0)
'division by zero'

這個例子表明，invert中的print表達式永遠不會求值，反之，控制流跳到了handler中的except子句組中。將ZeroDivisionError e強制轉為字符串會得到由handler: 'division by zero'返回的人類可讀的字符串。

3.4.1 異常對象

異常對象本身就帶有屬性，例如在assert語句中的錯誤信息，以及有關異常產生處的信息。用戶定義的異常類可以攜帶額外的屬性。

在第一章中，我們實現了牛頓法來尋找任何函數的零點。下面的例子定義了一個異常類，無論何時ValueError出現，它都返回迭代改進過程中所發現的最佳猜測值。數學錯誤（ValueError的一種）在sqrt在負數上調用時產生。這個異常由拋出IterImproveError處理，它將牛頓迭代法的最新猜測值儲存為參數。

首先，我們定義了新的類，繼承自Exception。

>>> class IterImproveError(Exception):
        def __init__(self, last_guess):
            self.last_guess = last_guess

下面，我們定義了IterImprove，我們的通用迭代改進算法的一個版本。這個版本通過拋出IterImproveError異常，儲存最新的猜測值來處理任何ValueError。像之前一樣，iter_improve接受兩個函數作為參數，每個函數都接受單一的數值參數。update函數返回新的猜測值，而done函數返回布爾值，表明改進是否收斂到了正確的值。

>>> def iter_improve(update, done, guess=1, max_updates=1000):
        k = 0
        try:
            while not done(guess) and k < max_updates:
                guess = update(guess)
                k = k + 1
            return guess
        except ValueError:
            raise IterImproveError(guess)

最後，我們定義了find_root，它返回iter_improve的結果。iter_improve應用於由newton_update返回的牛頓更新函數。newton_update定義在第一章，在這個例子中無需任何改變。find_root的這個版本通過返回它的最後一個猜測之來處理IterImproveError。

>>> def find_root(f, guess=1):
        def done(x):
            return f(x) == 0
        try:
            return iter_improve(newton_update(f), done, guess)
        except IterImproveError as e:
            return e.last_guess

考慮使用find_root來尋找2 * x ** 2 + sqrt(x)的零點。這個函數的一個零點是0，但是在任何負數上求解它會產生ValueError。我們第一章的牛頓法實現會產生異常，並且不能返回任何零點的猜測值。我們的修訂版實現在錯誤之前返回了最新的猜測值。

>>> from math import sqrt
>>> find_root(lambda x: 2*x*x + sqrt(x))
-0.030211203830201594

雖然這個近似值仍舊距離正確的答案0很遠，一些應用更傾向於這個近似值而不是ValueError。

異常是另一個技巧，幫助我們將程序細節劃分為模塊化的部分。在這個例子中，Python 的異常機制允許我們分離迭代改進的邏輯，它在try子句組中沒有發生改變，以及錯誤處理的邏輯，它出現在except子句中。我們也會發現，異常在使用 Python 實現解釋器時是個非常實用的特性。

3.5 組合語言的解釋器

來源：3.5 Interpreters for Languages with Combination

譯者：飛龍

協議：CC BY-NC-SA 4.0

運行在任何現代計算機上的軟件都以多種編程語言寫成。其中有物理語言，例如用於特定計算機的機器語言。這些語言涉及到基於獨立儲存位和原始機器指令的數據表示和控制。機器語言的程序員涉及到使用提供的硬件，為資源有限的計算構建系統和功能的高效實現。高階語言構建在機器語言之上，隱藏了表示為位集的數據，以及表示為原始指令序列的程序的細節。這些語言擁有例如過程定義的組合和抽象的手段，它們適用於組織大規模的軟件系統。

元語言抽象 -- 建立了新的語言 -- 並在所有工程設計分支中起到重要作用。它對於計算機編程尤其重要，因為我們不僅僅可以在編程中構想出新的語言，我們也能夠通過構建解釋器來實現它們。編程語言的解釋器是一個函數，它在語言的表達式上調用，執行求解表達式所需的操作。

我們現在已經開始了技術之旅，通過這種技術，編程語言可以建立在其它語言之上。我們首先會為計算器定義解釋器，它是一種受限的語言，和 Python 調用表達式具有相同的語法。我們之後會從零開始開發 Scheme 和 Logo 語言的解釋器，它們都是 Lisp 的方言，Lisp 是現在仍舊廣泛使用的第二老的語言。我們所創建的解釋器，在某種意義上，會讓我們使用 Logo 編寫完全通用的程序。為了這樣做，它會實現我們已經在這門課中開發的求值環境模型。

3.5.1 計算器

我們的第一種新語言叫做計算器，一種用於加減乘除的算術運算的表達式語言。計算器擁有 Python 調用表達式的語法，但是它的運算符對於所接受的參數數量更加靈活。例如，計算器運算符mul和add可接受任何數量的參數：

calc> add(1, 2, 3, 4)
10
calc> mul()
1

sub運算符擁有兩種行為：傳入一個運算符，它會對運算符取反。傳入至少兩個，它會從第一個參數中減掉剩餘的參數。div運算符擁有 Python 的operator.truediv的語義，只接受兩個參數。

calc> sub(10, 1, 2, 3)
4
calc> sub(3)
-3
calc> div(15, 12)
1.25

就像 Python 中那樣，調用表達式的嵌套提供了計算器語言中的組合手段。為了精簡符號，我們使用運算符的標準符號來代替名稱：

calc> sub(100, mul(7, add(8, div(-12, -3))))
16.0
calc> -(100, *(7, +(8, /(-12, -3))))
16.0

我們會使用 Python 實現計算器解釋器。也就是說，我們會編寫 Python 程序來接受字符串作為輸入，並返回求值結果。如果輸入是符合要求的計算器表達式，結果為字符串，反之會產生合適的異常。計算器語言解釋器的核心是叫做calc_eval的遞歸函數，它會求解樹形表達式對象。

**表達式樹。**到目前為止，我們在描述求值過程中所引用的表達式樹，還是概念上的實體。我們從沒有顯式將表達式樹表示為程序中的數據。為了編寫解釋器，我們必須將表達式當做數據操作。在這一章中，許多我們之前介紹過的概念都會最終以代碼實現。

計算器中的基本表達式只是一個數值，類型為int或float。所有複合表達式都是調用表達式。調用表達式表示為擁有兩個屬性實例的Exp類。計算器的operator總是字符串：算數運算符的名稱或符號。operands要麼是基本表達式，要麼是Exp的實例本身。

>>> class Exp(object):
        """A call expression in Calculator."""
        def __init__(self, operator, operands):
            self.operator = operator
            self.operands = operands
        def __repr__(self):
            return 'Exp({0}, {1})'.format(repr(self.operator), repr(self.operands))
        def __str__(self):
            operand_strs = ', '.join(map(str, self.operands))
            return '{0}({1})'.format(self.operator, operand_strs)

Exp實例定義了兩個字符串方法。__repr__方法返回 Python 表達式，而__str__方法返回計算器表達式。

>>> Exp('add', [1, 2])
Exp('add', [1, 2])
>>> str(Exp('add', [1, 2]))
'add(1, 2)'
>>> Exp('add', [1, Exp('mul', [2, 3, 4])])
Exp('add', [1, Exp('mul', [2, 3, 4])])
>>> str(Exp('add', [1, Exp('mul', [2, 3, 4])]))
'add(1, mul(2, 3, 4))'

最後的例子演示了Exp類如何通過包含作為operands元素的Exp的實例，來表示表達式樹中的層次結構。

求值。calc_eval函數接受表達式作為參數，並返回它的值。它根據表達式的形式為表達式分類，並且指導它的求值。對於計算器來說，表達式的兩種句法形式是數值或調用表達式，後者是Exp的實例。數值是自求值的，它們可以直接從calc_eval中返回。調用表達式需要使用函數。

>>> def calc_eval(exp):
        """Evaluate a Calculator expression."""
        if type(exp) in (int, float):
            return exp
        elif type(exp) == Exp:
            arguments = list(map(calc_eval, exp.operands))
            return calc_apply(exp.operator, arguments)

調用表達式首先通過將calc_eval函數遞歸映射到操作數的列表，計算出參數列表來求值。之後，在第二個函數calc_apply中，運算符會作用於這些參數上。

計算器語言足夠簡單，我們可以輕易地在單一函數中表達每個運算符的使用邏輯。在calc_apply中，每種條件子句對應一個運算符。

>>> from operator import mul
>>> from functools import reduce
>>> def calc_apply(operator, args):
        """Apply the named operator to a list of args."""
        if operator in ('add', '+'):
            return sum(args)
        if operator in ('sub', '-'):
            if len(args) == 0:
                raise TypeError(operator + ' requires at least 1 argument')
            if len(args) == 1:
                return -args[0]
            return sum(args[:1] + [-arg for arg in args[1:]])
        if operator in ('mul', '*'):
            return reduce(mul, args, 1)
        if operator in ('div', '/'):
            if len(args) != 2:
                raise TypeError(operator + ' requires exactly 2 arguments')
            numer, denom = args
            return numer/denom

上面，每個語句組計算了不同運算符的結果，或者當參數錯誤時產生合適的TypeError。calc_apply函數可以直接調用，但是必須傳入值的列表作為參數，而不是運算符表達式的列表。

>>> calc_apply('+', [1, 2, 3])
6
>>> calc_apply('-', [10, 1, 2, 3])
4
>>> calc_apply('*', [])
1
>>> calc_apply('/', [40, 5])
8.0

calc_eval的作用是，執行合適的calc_apply調用，通過首先計算操作數子表達式的值，之後將它們作為參數傳入calc_apply。於是，calc_eval可以接受嵌套表達式。

>>> e = Exp('add', [2, Exp('mul', [4, 6])])
>>> str(e)
'add(2, mul(4, 6))'
>>> calc_eval(e)
26

calc_eval的結構是個類型（表達式的形式）分發的例子。第一種表達式是數值，不需要任何的額外求值步驟。通常，基本表達式不需要任何額外的求值步驟，這叫做自求值。計算器語言中唯一的自求值表達式就是數值，但是在通用語言中可能也包括字符串、布爾值，以及其它。

**“讀取-求值-打印”循環。**和解釋器交互的典型方式是“讀取-求值-打印”循環（REPL），它是一種交互模式，讀取表達式、對其求值，之後為用戶打印出結果。Python 交互式會話就是這種循環的例子。

REPL 的實現與所使用的解釋器無關。下面的read_eval_print_loop函數使用內建的input函數，從用戶接受一行文本作為輸入。它使用語言特定的calc_parse函數構建表達式樹。calc_parse在隨後的解析一節中定義。最後，它打印出對由calc_parse返回的表達式樹調用calc_eval的結果。

>>> def read_eval_print_loop():
        """Run a read-eval-print loop for calculator."""
        while True:
            expression_tree = calc_parse(input('calc> '))
            print(calc_eval(expression_tree))

read_eval_print_loop的這個版本包含所有交互式界面的必要組件。一個樣例會話可能像這樣：

calc> mul(1, 2, 3)
6
calc> add()
0
calc> add(2, div(4, 8))
2.5

這個循環沒有實現終端或者錯誤處理機制。我們可以通過向用戶報告錯誤來改進這個界面。我們也可以允許用戶通過發射鍵盤中斷信號（Control-C），或文件末尾信號（Control-D）來退出循環。為了實現這些改進，我們將原始的while語句組放在try語句中。第一個except子句處理了由calc_parse產生的SyntaxError異常，也處理了由calc_eval產生的TypeError和ZeroDivisionError異常。

>>> def read_eval_print_loop():
        """Run a read-eval-print loop for calculator."""
        while True:
            try:
                expression_tree = calc_parse(input('calc> '))
                print(calc_eval(expression_tree))
            except (SyntaxError, TypeError, ZeroDivisionError) as err:
                print(type(err).__name__ + ':', err)
            except (KeyboardInterrupt, EOFError):  # <Control>-D, etc.
                print('Calculation completed.')
                return

這個循環實現報告錯誤而不退出循環。發生錯誤時不退出程序，而是在錯誤消息之後重新開始循環可以讓用戶回顧他們的表達式。通過導入readline模塊，用戶甚至可以使用上箭頭或Control-P來回憶他們之前的輸入。最終的結果提供了錯誤信息報告的界面：

calc> add
SyntaxError: expected ( after add
calc> div(5)
TypeError: div requires exactly 2 arguments
calc> div(1, 0)
ZeroDivisionError: division by zero
calc> ^DCalculation completed.

在我們將解釋器推廣到計算器之外的語言時，我們會看到，read_eval_print_loop由解析函數、求值函數，和由try語句處理的異常類型參數化。除了這些修改之外，任何 REPL 都可以使用相同的結構來實現。

3.5.2 解析

解析是從原始文本輸入生成表達式樹的過程。解釋這些表達式樹是求值函數的任務，但是解析器必須提供符合格式的表達式樹給求值器。解析器實際上由兩個組件組成，詞法分析器和語法分析器。首先，詞法分析器將輸入字符串拆成標記（token），它們是語言的最小語法單元，就像名稱和符號那樣。其次，語法分析器從這個標記序列中構建表達式樹。

>>> def calc_parse(line):
        """Parse a line of calculator input and return an expression tree."""
        tokens = tokenize(line)
        expression_tree = analyze(tokens)
        if len(tokens) > 0:
            raise SyntaxError('Extra token(s): ' + ' '.join(tokens))
        return expression_tree

標記序列由叫做tokenize的詞法分析器產生，並被叫做analyze語法分析器使用。這裡，我們定義了calc_parse，它只接受符合格式的計算器表達式。一些語言的解析器為接受以換行符、分號或空格分隔的多種表達式而設計。我們在引入 Logo 語言之前會推遲實現這種複雜性。

**詞法分析。**用於將字符串解釋為標記序列的組件叫做分詞器（tokenizer ），或者詞法分析器。在我們的視線中，分詞器是個叫做tokenize的函數。計算器語言由包含數值、運算符名稱和運算符類型的符號（比如+）組成。這些符號總是由兩種分隔符劃分：逗號和圓括號。每個符號本身都是標記，就像每個逗號和圓括號那樣。標記可以通過向輸入字符串添加空格，之後在每個空格處分割字符串來分開。

>>> def tokenize(line):
        """Convert a string into a list of tokens."""
        spaced = line.replace('(',' ( ').replace(')',' ) ').replace(',', ' , ')
        return spaced.split()

對符合格式的計算器表達式分詞不會損壞名稱，但是會分開所有符號和分隔符。

>>> tokenize('add(2, mul(4, 6))')
['add', '(', '2', ',', 'mul', '(', '4', ',', '6', ')', ')']

擁有更加複合語法的語言可能需要更復雜的分詞器。特別是，許多分析器會解析每種返回標記的語法類型。例如，計算機中的標記類型可能是運算符、名稱、數值或分隔符。這個分類可以簡化標記序列的解析。

**語法分析。**將標記序列解釋為表達式樹的組件叫做語法分析器。在我們的實現中，語法分析由叫做analyze的遞歸函數完成。它是遞歸的，因為分析標記序列經常涉及到分析這些表達式樹中的標記子序列，它本身作為更大的表達式樹的子分支（比如操作數）。遞歸會生成由求值器使用的層次結構。

analyze函數接受標記列表，以符合格式的表達式開始。它會分析第一個標記，將表示數值的字符串強制轉換為數字的值。之後要考慮計算機中的兩個合法表達式類型。數字標記本身就是完整的基本表達式樹。複合表達式以運算符開始，之後是操作數表達式的列表，由圓括號分隔。我們以一個不檢查語法錯誤的實現開始。

>>> def analyze(tokens):
        """Create a tree of nested lists from a sequence of tokens."""
        token = analyze_token(tokens.pop(0))
        if type(token) in (int, float):
            return token
        else:
            tokens.pop(0)  # Remove (
            return Exp(token, analyze_operands(tokens))
>>> def analyze_operands(tokens):
        """Read a list of comma-separated operands."""
        operands = []
        while tokens[0] != ')':
            if operands:
                tokens.pop(0)  # Remove ,
            operands.append(analyze(tokens))
        tokens.pop(0)  # Remove )
        return operands

最後，我們需要實現analyze_token。analyze_token函數將數值文本轉換為數值。我們並不自己實現這個邏輯，而是依靠內建的 Python 類型轉換，使用int和float構造器來將標記轉換為這種類型。

>>> def analyze_token(token):
        """Return the value of token if it can be analyzed as a number, or token."""
        try:
            return int(token)
        except (TypeError, ValueError):
            try:
                return float(token)
            except (TypeError, ValueError):
                return token

我們的analyze實現就完成了。它能夠正確將符合格式的計算器表達式解析為表達式樹。這些樹由str函數轉換回計算器表達式。

>>> expression = 'add(2, mul(4, 6))'
>>> analyze(tokenize(expression))
Exp('add', [2, Exp('mul', [4, 6])])
>>> str(analyze(tokenize(expression)))
'add(2, mul(4, 6))'

analyze函數只會返回符合格式的表達式樹，並且它必須檢測輸入中的語法錯誤。特別是，它必須檢測表達式是否完整、正確分隔，以及只含有已知的運算符。下面的修訂版本確保了語法分析的每一步都找到了預期的標記。

>>> known_operators = ['add', 'sub', 'mul', 'div', '+', '-', '*', '/']
>>> def analyze(tokens):
        """Create a tree of nested lists from a sequence of tokens."""
        assert_non_empty(tokens)
        token = analyze_token(tokens.pop(0))
        if type(token) in (int, float):
            return token
        if token in known_operators:
            if len(tokens) == 0 or tokens.pop(0) != '(':
                raise SyntaxError('expected ( after ' + token)
            return Exp(token, analyze_operands(tokens))
        else:
            raise SyntaxError('unexpected ' + token)
>>> def analyze_operands(tokens):
        """Analyze a sequence of comma-separated operands."""
        assert_non_empty(tokens)
        operands = []
        while tokens[0] != ')':
            if operands and tokens.pop(0) != ',':
                raise SyntaxError('expected ,')
            operands.append(analyze(tokens))
            assert_non_empty(tokens)
        tokens.pop(0)  # Remove )
        return elements
>>> def assert_non_empty(tokens):
        """Raise an exception if tokens is empty."""
        if len(tokens) == 0:
            raise SyntaxError('unexpected end of line')

信息豐富的語法錯誤在本質上提升瞭解釋器的可用性。在上面，SyntaxError 異常包含所發生的問題描述。這些錯誤字符串也用作這些分析函數的定義文檔。

這個定義完成了我們的計算器解釋器。你可以獲取單獨的 Python 3 源碼 calc.py來測試。我們的解釋器對錯誤的處理能力很強，用戶在calc>提示符後面的每個輸入都會求值為數值，或者產生合適的錯誤，描述輸入為什麼不是符合格式的計算器表達式。

3.6 抽象語言的解釋器

來源：3.6 Interpreters for Languages with Abstraction

譯者：飛龍

協議：CC BY-NC-SA 4.0

計算器語言提供了一種手段，來組合一些嵌套的調用表達式。然而，我們卻沒有辦法定義新的運算符，將值賦給名稱，或者表達通用的計算方法。總之，計算器並不以任何方式支持抽象。所以，它並不是特別強大或通用的編程語言。我們現在轉到定義一種通用編程語言的任務中，這門語言通過將名稱綁定到值以及定義新的操作來支持抽象。

我們並不是進一步擴展簡單的計算器語言，而是重新開始，並且為 Logo 語言開發解釋器。Logo 並不是為這門課發明的語言，而是一種經典的命令式語言，擁有許多解釋器實現和自己的開發者社區。

上一章，我們將完整的解釋器表示為 Python 源碼，這一章使用描述性的方式。某個配套工程需要你通過構建完整的 Logo 函數式解釋器來實現這裡展示的概念。

3.6.1 Scheme 語言

Scheme 是 Lisp 的一種方言，Lisp 是現在仍在廣泛使用的第二老（在 Fortran 之後）的編程語言。Scheme首次在 1975 年由 Gerald Sussman 和 Guy Steele 描述。Revised(4) Report on the Algorithmic Language Scheme 的引言中寫道：

編程語言不應該通過堆砌特性，而是應該通過移除那些使額外特性變得必要的缺點和限制來設計。Scheme 表明，用於組成表達式的非常少量的規則，在沒有組合方式的限制的情況下，足以組成實用並且高效的編程語言，它足夠靈活，在使用中可以支持多數當今的主流編程範式。

我們將這個報告推薦給你作為 Scheme 語言的詳細參考。我們這裡只會涉及重點。下面的描述中，我們會用到報告中的例子。

雖然 Scheme 非常簡單，但它是一種真正的編程語言，在許多地方都類似於 Python，但是“語法糖[1]”會盡量少。基本上，所有運算符都是函數調用的形式。這裡我們會描述完整的 Scheme 語言的在報告中描述的可展示的子集。

[1] 非常遺憾，這對於 Scheme 語言的最新版本並不成立，就像 Revised(6) Report 中的那樣。所以這裡我們僅僅針對之前的版本。

Scheme 有多種可用的實現，它們添加了額外的過程。在 UCB，我們使用Stk 解釋器的一個修改版，它也在我們的教學服務器上以stk提供。不幸的是，它並不嚴格遵守正式規範，但它可用於我們的目的。

**使用解釋器。**就像 Python 解釋器[2]那樣，向 Stk 鍵入的表達式會由“讀取-求值-打印”循環求值並打印：

>>> 3
3
>>> (- (/ (* (+ 3 7 10) (- 1000 8)) 992) 17)
3
>>> (define (fib n) (if (< n 2) n (+ (fib (- n 2)) (fib (- n 1)))))
fib
>>> '(1 (7 19))
(1 (7 19))

[2] 在我們的例子中，我們使用了和 Python 相同的符號>>>和...，來表示解釋器的輸入行，和非前綴輸出的行。實際上，Scheme 解釋器使用不同的提示符。例如，Stk 以STk>來提示，並且不提示連續行。然而 Python 的慣例使輸入和輸出更加清晰。

**Scheme 中的值。**Scheme 中的值通常與 Python 對應。

布爾值

真值和假值，使用#t和#f來表示。Scheme 中唯一的假值（按照 Python 的含義）就是#f。

數值

這包括任意精度的整數、有理數、複數，和“不精確”（通常是浮點）數值。整數可用標準的十進制表示，或者通過在數字之前添加#o（八進制）、#x（十六進制）或#b（二進制），以其他進製表示。

符號

符號是一種字符串，但是不被引號包圍。有效的字符包括字母、數字和：

!  $  %  &  *  /  :  <  = >  ?  ^  _  ~  +  -  .  @

在使用read函數輸入時，它會讀取 Scheme 表達式（也是解釋器用於輸入程序文本的東西），不區分符號中的大小寫（在STk 實現中會轉為小寫）。兩個帶有相同表示的符號表示同一對象（並不是兩個碰巧擁有相同內容的對象）。

偶對和列表

偶對是含有兩個（任意類型）成員的對象，叫做它的car和cdr。car為A且cdr為B的偶對可表示為(A . B)。偶對（就像 Python 中的元組）可以表示列表、樹和任意的層次結構。

標準的 Scheme 列表包含空的列表值（記為()），或者包含一個偶對，它的car是列表第一個元素，cdr是列表的剩餘部分。所以，包含整數1, 2, 3的列表可表示為：

(1 . (2 . (3 . ())))

列表無處不在，Scheme 允許我們將(a . ())縮略為(a)，將(a . (b ...))縮略為(a b ...)。所以，上面的列表通常寫為：

(1 2 3)

過程（函數）

就像 Python 中一樣，過程（或函數）值表示一些計算，它們可以通過向函數提供參數來調用。過程要麼是原始的，由 Scheme 的運行時系統提供，要麼從 Scheme 表達式和環境構造（就像 Python 中那樣）。沒有用於函數值的直接表示，但是有一些綁定到基本函數的預定義標識符，也有一些 Scheme 表達式，在求值時會產生新的過程值。

其它類型

Scheme 也支持字符和字符串（類似 Python 的字符串，除了 Scheme 區分字符和字符串），以及向量（就像 Python 的列表）。

**程序表示。**就像其它 Lisp 版本，Scheme 的數據值也用於表示程序。例如，下面的 Scheme 列表：

(+ x (* 10 y))

取決於如何使用，可表示為三個元素的列表（它的最後一個元素也是三個元素的列表），或者表達為用於計算x+10y的 Scheme 表達式。為了將 Scheme 值求值為程序，我們需要考慮值的類型，並按以下步驟求值：

• 整數、布爾值、字符、字符串和向量都求值為它們自己。所以，表達式5求值為 5。
• 純符號看做變量。它們的值由當前被求值環境來決定，就像 Python 那樣。
• 非空列表以兩種方式解釋，取決於它們的第一個成員：
  • 如果第一個成員是特殊形式的符號（在下面描述），求值由這個特殊形式的規則執行。
  • 所有其他情況（叫做組合）中，列表的成員會以非特定的順序（遞歸）求值。第一個成員必須是函數值。這個值會被調用，以列表中剩餘成員的值作為參數。
• 其他 Scheme 值（特別是，不是列表的偶對）在程序中是錯誤的。

例如：

>>> 5              ; A literal.
5
>>> (define x 3)   ; A special form that creates a binding for symbol
x                   ; x.
>>> (+ 3 (* 10 x)) ; A combination.  Symbol + is bound to the primitive
33                  ; add function and * to primitive multiply.

**基本的特殊形式。**特殊形式將東西表示為 Python 中的控制結構、函數調用或者類的定義：在調用時，這些結構不會簡單地立即求值。

首先，一些通用的結構以這種形式使用：

EXPR-SEQ

只是表達式的序列，例如：

(+ 3 2) x (* y z)

當它出現在下面的定義中時，它指代從左到右求值的表達式序列，序列中最後一個表達式的值就是它的值。

BODY

一些結構擁有“主體”，它們是 EXPR-SEQ，就像上面一樣，可能由一個或多個定義處理。它們的值就是 EXPR-SEQ 的值。這些定義的解釋請見內部定義一節。

下面是這些特殊形式的代表性子集：

定義

定義可以出現在程序的頂層（也就是不包含在其它結構中）。

(define SYM EXPR)

求出EXPR並在當前環境將其值綁定到符號SYM上。

(define (SYM ARGUMENTS) BODY)

等價於(define SYM (lambda (ARGUMENTS) BODY))。

(lambda (ARGUMENTS) BODY)

求值為函數。ARGUMENTS 通常為（可能非空的）不同符號的列表，向函數提供參數名稱，並且表明它們的數量。ARGUMENTS也可能具有如下形式：

(sym1 sym2 ... symn . symr)

（也就是說，列表的末尾並不像普通列表那樣是空的，最後的cdr是個符號。）這種情況下，symr會綁定到列表的尾後參數值（後面的第 n+1 個參數）。

當產生的函數被調用時，ARGUMENTS在一個新的環境中綁定到形參的值上，新的環境擴展自lambda表達式求值的環境（就像 Python 那樣）。之後BODY會被求值，它的值會作為調用的值返回。

(if COND-EXPR TRUE-EXPR OPTIONAL-FALSE-EXPR)

求出COND-EXPR，如果它的值不是#f，那麼求出TRUE-EXPR，結果會作為if的值。如果COND-EXPR值為#f而且OPTIONAL-FALSE-EXPR存在，它會被求值為並作為if的值。如果它不存在，if值是未定義的。

(set! SYMBOL EXPR)

求出EXPR使用該值替換SYMBOL 的綁定。SYMBOL 必須已經綁定，否則會出現錯誤。和 Python 的默認情況不同，它會在定義它的第一個環境幀上替換綁定，而不總是最深處的幀。

(quote EXPR) 或 'EXPR

將 Scheme 數據結構用於程序表示的一個問題，是需要一種方式來表示打算被求值的程序文本。quote形式求值為EXPR自身，而不進行進一步的求值（替代的形式使用前導的單引號，由 Scheme 表達式讀取器轉換為第一種形式）。例如：

>>> (+ 1 2)
3
>>> '(+ 1 2)
(+ 1 2)
>>> (define x 3)
x
>>> x
3
>>> (quote x)
x
>>> '5
5
>>> (quote 'x)
(quote x)

派生的特殊形式

派生結構時可以翻譯為基本結構的結構。它們的目的是讓程序對於讀取器更加簡潔可讀。在 Scheme 中：

(begin EXPR-SEQ)

簡單地求值併產生EXPR-SEQ的值。這個結構是個簡單的方式，用於在需要單個表達式的上下文中執行序列或表達式。

(and EXPR1 EXPR2 ...)

每個EXPR從左到右執行，直到碰到了#f，或遍歷完EXPRs。值是最後求值的EXPR，如果EXPRs列表為空，那麼值為#t。例如：

>>> (and (= 2 2) (> 2 1))
#t
>>> (and (< 2 2) (> 2 1))
#f
>>> (and (= 2 2) '(a b))
(a b)
>>> (and)
#t

(or EXPR1 EXPR2 ...)

每個EXPR從左到右求值，直到碰到了不為#f的值，或遍歷完EXPRs。值為最後求值的EXPR，如EXPRs列表為空，那麼值為#f。例如：

>>> (or (= 2 2) (> 2 3))
#t
>>> (or (= 2 2) '(a b))
#t
>>> (or (> 2 2) '(a b))
(a b)
>>> (or (> 2 2) (> 2 3))
#f
>>> (or)
#f

(cond CLAUSE1 CLAUSE2 ...)

每個CLAUSEi都依次處理，直到其中一個處理成功，它的值就是cond的值。如果沒有子句處理成功，值是未定義的。每個子句都有三種可能的形式。

如果TEST-EXPR 求值為不為#f的值，(TEST-EXPR EXPR-SEQ)形式執行成功。這種情況下，它會求出EXPR-SEQ併產生它的值。EXPR-SEQ可以不寫，這種情況下值為TEST-EXPR本身。

最後一個子句可為(else EXPR-SEQ)的形式，它等價於(#t EXPR-SEQ)。

最後，如果(TEST_EXPR => EXPR)的形式在TEST_EXPR求值為不為#f的值（叫做V）時求值成功。如果求值成功，cond結構的值是由(EXPR V)返回的值。也就是說，EXPR必須求值為單參數的函數，在TEST_EXPR的值上調用。

例如：

>>> (cond ((> 3 2) 'greater)
...        ((< 3 2) 'less)))
greater
>>> (cond ((> 3 3) 'greater)
...        ((< 3 3) 'less)
...        (else 'equal))
equal
>>> (cond ((if (< -2 -3) #f -3) => abs)
...        (else #f))
3

(case KEY-EXPR CLAUSE1 CLAUSE2 ...)

KEY-EXPR的求值會產生一個值K。之後將K與每個CLAUSEi一次匹配，直到其中一個成功，並且返回該子句的值。如果沒有子句成功，值是未定義的。每個子句都擁有((DATUM1 DATUM2 ...) EXPR-SEQ)的形式。其中DATUMs是 Scheme 值（它們不會被求值）。如果K匹配了DATUM的值之一（由下面描述的eqv?函數判斷），子句就會求值成功，它的EXPR-SEQ就會被求值，並且它的值會作為case的值。最後的子句可為(else EXPR-SEQ)的形式，它總是會成功，例如：

>>> (case (* 2 3)
...     ((2 3 5 7) 'prime)
...     ((1 4 6 8 9) 'composite))
composite
>>> (case (car '(a . b))
...     ((a c) 'd)
...     ((b 3) 'e))
d
>>> (case (car '(c d))
...    ((a e i o u) 'vowel)
...    ((w y) 'semivowel)
...    (else 'consonant))
consonant

(let BINDINGS BODY)

BINDINGS是偶對的列表，形式為：

( (VAR1 INIT1) (VAR2 INIT2) ...)

其中VARs是（不同的）符號，而INITs是表達式。首先會求出INIT表達式，之後創建新的幀，將這些值綁定到VARs，再然後在新環境中求出BODY，返回它的值。換句話說，它等價於調用

((lambda (VAR1 VAR2 ...) BODY)
INIT1 INIT2 ...)

所以，任何INIT表達式中的VARs引用都指向這些符號在let結構外的定義（如果存在的話），例如：

>>> (let ((x 2) (y 3))
...       (* x y))
6
>>> (let ((x 2) (y 3))
...       (let ((x 7) (z (+ x y)))
...            (* z x)))
35

(let* BINDINGS BODY)

BINDINGS 的語法和let相同。它等價於

(let ((VAR1 INIT1))
...
(let ((VARn INITn))
BODY))

也就是說，它就像let表達式那樣，除了VAR1的新綁定對INITs子序列以及BODY中可見，VAR2與之類似，例如：

>>> (define x 3)
x
>>> (define y 4)
y
>>> (let ((x 5) (y (+ x 1))) y)
4
>>> (let* ((x 5) (y (+ x 1))) y)
6

(letrec BINDINGS BODY)

同樣，語法類似於let。這裡，首先會創建新的綁定（帶有未定義的值），之後INITs被求值並賦給它們。如果某個INITs使用了某個VAR的值，並且沒有為其賦初始值，結果是未定義的。這個形式主要用於定義互相遞歸的函數（lambda 本身並不會使用它們提到過的值；這隻會在它們被調用時隨後發生）。例如：

(letrec ((even?
      (lambda (n)
             (if (zero? n)
                  #t
                  (odd? (- n 1)))))
     (odd?
      (lambda (n)
              (if (zero? n)
                  #f
                  (even? (- n 1))))))
(even? 88))

**內部定義。**當BODY以define結構的序列開始時，它們被看作“內部定義”，並且在解釋上與頂層定義有些不同。特別是，它們就像letrec那樣。

• 首先，會為所有由define語句定義的名稱創建綁定，一開始綁定到未定義的值上。
• 之後，值由定義來填充。

所以，內部函數定義的序列是互相遞歸的，就像 Python 中嵌套在函數中的def`語句那樣：

>>> (define (hard-even? x)     ;; An outer-level definition
...      (define (even? n)      ;; Inner definition
...          (if (zero? n)
...              #t
...              (odd? (- n 1))))
...      (define (odd? n)       ;; Inner definition
...          (if (zero? n)
...              #f
...              (even? (- n 1))))
...      (even? x))
>>> (hard-even? 22)
#t

**預定義函數。**預定義函數有很多，都在全局環境中綁定到名稱上，我們只會展示一小部分。其餘的會在 Revised(4) Scheme 報告中列出。函數調用並不是“特殊的”，因為它們都使用相同的完全統一的求值規則：遞歸求出所有項目（包括運算符），並且之後在操作數的值上調用運算符的值（它必須是個函數）。

• **算數：**Scheme 提供了標準的算數運算符，許多都擁有熟悉的表示，雖然它們統一出現在操作數前面：

  >>> ; Semicolons introduce one-line comments.
  >>> ; Compute (3+7+10)*(1000-8) // 992 - 17
  >>> (- (quotient (* (+ 3 7 10) (- 1000 8))) 17)
  3
  >>> (remainder 27 4)
  3
  >>> (- 17)
  -17
  

  與之相似，存在通用的數學比較運算符，為可接受多於兩個參數而擴展：

  >>> (< 0 5)
  #t
  >>> (>= 100 10 10 0)
  #t
  >>> (= 21 (* 7 3) (+ 19 2))
  #t
  >>> (not (= 15 14))
  #t
  >>> (zero? (- 7 7))
  #t
  

  隨便提一下，not是個函數，並不是and或or的特殊形式，因為他的運算符必須求值，所以不需要特殊對待。

• **列表和偶對。**很多操作用於處理偶對和列表（它們同樣由偶對和空列表構建）。

  >>> (cons 'a 'b)
  (a . b)
  >>> (list 'a 'b)
  (a b)
  >>> (cons 'a (cons 'b '()))
  (a b)
  >>> (car (cons 'a 'b))
  a
  >>> (cdr (cons 'a 'b))
  b
  >>> (cdr (list a b))
  (b)
  >>> (cadr '(a b))   ; An abbreviation for (car (cdr '(a b)))
  b
  >>> (cddr '(a b))   ; Similarly, an abbreviation for (cdr (cdr '(a b)))
  ()
  >>> (list-tail '(a b c) 0)
  (a b c)
  >>> (list-tail '(a b c) 1)
  (b c)
  >>> (list-ref '(a b c) 0)
  a
  >>> (list-ref '(a b c) 2)
  c
  >>> (append '(a b) '(c d) '() '(e))
  (a b c d e)
  >>> ; All but the last list is copied.  The last is shared, so:
  >>> (define L1 (list 'a 'b 'c))
  >>> (define L2 (list 'd))
  >>> (define L3 (append L1 L2))
  >>> (set-car! L1 1)
  >>> (set-car! L2 2)
  >>> L3
  (a b c 2)
  >>> (null? '())
  #t
  >>> (list? '())
  #t
  >>> (list? '(a b))
  #t
  >>> (list? '(a . b))
  #f
  

• 相等性：=運算符用於數值。通常對於值的相等性，Scheme 區分eq?（就像 Python 的is），eqv?（與之類似，但是和數值上的=一樣），和equal?（比較列表結構或字符串的內容）。通常來說，除了在比較符號、布爾值或者空列表的情況中，我們都使用eqv?和equal?。

  >>> (eqv? 'a 'a)
  #t
  >>> (eqv? 'a 'b)
  #f
  >>> (eqv? 100 (+ 50 50))
  #t
  >>> (eqv? (list 'a 'b) (list 'a 'b))
  #f
  >>> (equal? (list 'a 'b) (list 'a 'b))
  #t
  

• **類型。**每個值的類型都只滿足一個基本的類型斷言。

  >>> (boolean? #f)
  #t
  >>> (integer? 3)
  #t
  >>> (pair? '(a b))
  #t
  >>> (null? '())
  #t
  >>> (symbol? 'a)
  #t
  >>> (procedure? +)
  #t
  

• **輸入和輸出：**Scheme 解釋器通常執行“讀取-求值-打印”循環，但是我們可以在程序控制下顯式輸出東西，使用與解釋器內部相同的函數：

  >>> (begin (display 'a) (display 'b) (newline))
  ab
  

  於是，(display x)與 Python 的

  print(str(x), end="")
  

  相似，並且(newline)類似於print()。

  對於輸入來說，(read)從當前“端口”讀取 Scheme 表達式。它並不會解釋表達式，而是將其讀作數據：

  >>> (read)
  >>> (a b c)
  (a b c)
  

• 求值。apply 函數提供了函數調用運算的直接訪問：

  >>> (apply cons '(1 2))
  (1 . 2)
  >>> ;; Apply the function f to the arguments in L after g is
  >>> ;; applied to each of them
  >>> (define (compose-list f g L)
  ...     (apply f (map g L)))
  >>> (compose-list + (lambda (x) (* x x)) '(1 2 3))
  14
  

  這個擴展允許開頭出現“固定”參數：

  >>> (apply + 1 2 '(3 4 5))
  15
  

  下面的函數並不在 Revised(4) Scheme 中，但是存在於我們的解釋器版本中（警告：非標準的過程在 Scheme 的後續版本中並不以這種形式定義）：

  >>> (eval '(+ 1 2))
  3
  

  也就是說，eval求解一塊 Scheme 數據，它表示正確的 Scheme 表達式。這個版本在全局環境中求解表達式的參數。我們的解釋器也提供了一種方式，來規定求值的特定環境：

  >>> (define (incr n) (lambda (x) (+ n x)))
  >>> (define add5 (incr 5))
  >>> (add5 13)
  18
  >>> (eval 'n (procedure-environment add5))
  5
  

3.6.2 Logo 語言

Logo 是 Lisp 的另一種方言。它為教育用途而設計，所以 Logo 的許多設計決策是為了讓語言對新手更加友好。例如，多數 Logo 過程以前綴形式調用（首先是過程名稱，其次是參數），但是通用的算術運算符以普遍的中綴形式提供。Logo 的偉大之處是，它的簡單親切的語法仍舊為高級程序員提供了驚人的表現力。

Logo 的核心概念是，它的內建容器類型，也就是 Logo sentence （也叫作列表），可以輕易儲存 Logo 源碼，這也是它的強大表現力的來源。Logo 的程序可以編寫和執行 Logo 表達式，作為求值過程的一部分。許多動態語言都支持代碼生成，包括 Python，但是沒有語言像 Logo 一樣使代碼生成如此有趣和易用。

你可能希望下載完整的 Logo 解釋器來體驗這個語言。標準的實現是 Berkeley Logo（也叫做 UCBLogo），由 Brian Harvey 和他的 Berkeley 學生開發。對於蘋果用戶，ACSLogo 兼容 Mac OSX 的最新版本，並帶有一份介紹 Logo 語言許多特性的用戶指南。

**基礎。**Logo 設計為會話式。它的讀取-求值循環的提示符是一個問號（?），產生了“我下面應該做什麼？”的問題。我們自然想讓它打印數值：

? print 5
5

Logo 語言使用了非標準的調用表達式語法，完全不帶括號分隔符。上面，參數5轉給了print，它打印了它的參數。描述 Logo 程序結構的術語有些不同於 Python。Logo 擁有過程而不是 Python 中等價的函數，而且過程輸出值而不是返回值。和 python 類似，print過程總是輸出None，但也打印出參數的字符串表示作為副作用。（過程的參數在 Logo 中也通常叫做輸入，但是為了清晰起見，這篇文章中我們仍然稱之為參數。）

Logo 中最常見的數據類型是單詞，它是不帶空格的字符串。單詞用作可以表示數值、名稱和布爾值的通用值。可以解釋為數值或布爾值的記號，比如5，直接求值為單詞。另一方面，類似five的名稱解釋為過程調用：

? 5
You do not say what to do with 5.
? five
I do not know how to five.

5和five以不同方式解釋，Logo 的讀取-求值循環也以不同方式報錯。第一種情況的問題是，Logo 在頂層表達式不求值為 None 時報錯。這裡，我們看到了第一個 Logo 不同於計算器的結構；前者的接口是讀取-解釋循環，期待用戶來打印結果。後者使用更加通用的讀取-求值-打印循環，自動打印出返回值。Python 採取了混合的方式，非None的值使用repr強制轉換為字符串並自動打印。

Logo 的行可以順序包含多個表達式。解釋器會一次求出每個表達式。如果行中任何頂層表達式不求值為None，解釋器會報錯。一旦發生錯誤，行中其餘的表達式會被忽略。

? print 1 print 2
1
2
? 3 print 4
You do not say what to do with 3.

Logo 的調用表達式可以嵌套。在 Logo 的實現版本中，每個過程接受固定數量的參數。所以，當嵌套調用表達式的操作數完整時，Logo 解釋器能夠唯一地判斷。例如，考慮兩個過程sum和difference，它們相應輸出兩個參數的和或差。

? print sum 10 difference 7 3
14

我們可以從這個嵌套的例子中看到，分隔調用表達式的圓括號和逗號不是必須的。在計算器解釋器中，標點符號允許我們將表達式樹構建為純粹的句法操作，沒有任何運算符名稱的判斷。在 Logo 中，我們必須使用我們的知識，關於每個過程接受多少參數，來得出嵌套表達式的正確結構。下一節中，問題的細節會深入探討。

Logo 也支持中綴運算符，例如+和*。這些運算符的優先級根據代數的標準規則來解析。乘法和除法優於加法和減法：

? 2 + 3 * 4
14

如何實現運算符優先級和前綴運算符來生成正確的表達式樹的細節留做練習。對於下面的討論，我們會專注於使用前綴語法的調用表達式。

**引用。**一個名稱會被解釋為調用表達式的開始部分，但是我們也希望將單詞引用為數據。以雙引號開始的記號解釋為單詞字面值。要注意單詞字面值在 Logo 中並沒有尾後的雙引號。

? print "hello
hello

在 Lisp 的方言中（而 Logo 是它的方言），任何不被求值的表達式都叫做引用。這個引用的概念來自於事物之間的經典哲學。例如一隻狗，它可以到處亂跑和叫喚，而單詞“狗”只是用於指代這種事物的語言結構。當我們以引號使用“狗”的時候，我們並不是指特定的哪一隻，而是這個單詞。在語言中，引號允許我們談論語言自身，Logo 中也一樣。我們可以按照名稱引用sum過程，而不會實際調用它，通過這樣引用它：

? print "sum
sum

除了單詞，Logo 包含句子類型，可以叫做列表。句子由方括號包圍。print過程並不會打印方括號，以維持 Logo 的慣例風格，但是方括號可以使用show過程打印到輸出：

? print [hello world]
hello world
? show [hello world]
[hello world]

句子也可以使用三個不同的二元過程來構造。sentence過程將參數組裝為句子。它是多態過程，如果參數是單詞，會將它的參數放入新的句子中；如果參數是句子，則會將拼接參數。結果通常是一個句子：

? show sentence 1 2
[1 2]
? show sentence 1 [2 3]
[1 2 3]
? show sentence [1 2] 3
[1 2 3]
? show sentence [1 2] [3 4]
[1 2 3 4]

list過程從兩個元素創建句子，它允許用戶創建層次數據結構：

? show list 1 2
[1 2]
? show list 1 [2 3]
[1 [2 3]]
? show list [1 2] 3
[[1 2] 3]
? show list [1 2] [3 4]
[[1 2] [3 4]]

最後，fput過程從第一個元素和列表的剩餘部分創建列表，就像這一章之前的 Python RList構造器那樣：

? show fput 1 [2 3]
[1 2 3]
? show fput [1 2] [3 4]
[[1 2] 3 4]

我們在 Logo 中可以調用sentence、list和fput句子構造器。在 Logo 中將句子解構為first和剩餘部分（叫做butfirst）也非常直接，所以，我們也擁有一系列句子的選擇器過程。

? print first [1 2 3]
1
? print last [1 2 3]
3
? print butfirst [1 2 3]
[2 3]

**作為數據的表達式。**句子的內容可以直接當做未求值的引用。所以，我們可以打印出 Logo 表達式而不求值：

? show [print sum 1 2]
[print sum 1 2]

將 Logo 表示表達式表示為句子的目的通常不是打印它們，而是使用run過程來求值。

? run [print sum 1 2]
3

通過組合引用和句子構造器，以及run過程，我們獲得了一個非常通用的組合手段，它憑空構建 Logo 表達式並對其求值：

? run sentence "print [sum 1 2]
3
? print run sentence "sum sentence 10 run [difference 7 3]
14

最後一個例子的要點是為了展示，雖然sum和difference過程在 Logo 中並不是一等的構造器（它們不能直接放在句子中），它們的名稱是一等的，並且run過程可以將它們的名稱解析為所引用的過程。

將代碼表示為數據，並且稍後將其解釋為程序的一部分的功能，是 Lisp 風格語言的特性。程序可以重新編寫自己來執行是一個強大的概念，並且作為人工智能（AI）早期研究的基礎。Lisp 在數十年間都是 AI 研究者的首選語言。Lisp 語言由 John McCarthy 發明，他也發明了“人工智能”術語，並且在該領域的定義中起到關鍵作用。Lisp 方言的“代碼即數據”的特性，以及它們的簡潔和優雅，今天仍繼續吸引著 Lisp 程序員。

**海龜製圖（Turtle graphics）。**所有 Logo 的實現都基於 Logo 海龜 來完成圖形輸出。這個海龜以畫布的中點開始，基於過程移動和轉向，並且在它的軌跡上畫線。雖然海龜為鼓勵青少年實踐編程而發明，它對於高級程序員來說也是有趣的圖形化工具。

在執行 Logo 程序的任意時段，Logo 海龜都在畫布上擁有位置和朝向。類似於forward和right的一元過程能修改海龜的位置和朝向。常用的過程都有縮寫：forward也叫作fd，以及其它。下面的嵌套表達式畫出了每個端點帶有小星星的大星星：

? repeat 5 [fd 100 repeat 5 [fd 20 rt 144] rt 144]

海龜過程的全部指令也內建於 Python 的turtle模塊中。這些函數的有限子集也在這一章的配套項目中提供。

**賦值。**Logo 支持綁定名稱和值。就像 Python 中那樣，Logo 環境由幀的序列組成，每個幀中的某個名稱都最多綁定到一個值上。名稱使用make過程來綁定，它接受名稱和值作為參數。

? make "x 2

任何以冒號起始的單詞，例如:x都叫做變量。變量求值為其名稱在當前環境中綁定的值。

make過程和 Python 的賦值語句具有不同的作用。傳遞給make的名稱要麼已經綁定了值，要麼當前未綁定。

1. 如果名稱已經綁定，make在找到它的第一幀中重新綁定該名稱。
2. 如果沒有綁定，make在全局幀中綁定名稱。

這個行為與 Python 賦值語句的語義很不同，後者總是在當前環境中的第一幀中綁定名稱。上面的第一條規則類似於遵循nonlocal語句的 Python 賦值。第二條類似於遵循global語句的全局賦值。

**過程。**Logo 支持用戶使用以to關鍵字開始的定義來定義過程。定義是 Logo 中的最後一個表達式類型，在調用表達式、基本表達式和引用表達式之後。定義的第一行提供了新過程的名稱，隨後是作為變量的形參。下面的行是過程的主體，它可以跨越多行，並且必須以只包含end記號的一行結束。Logo 的讀取-求值循環使用>連接符來提示用戶輸入過程體。用戶定義過程使用output過程來輸出一個值。

? to double :x
> output sum :x :x
> end
? print double 4
8

Logo 的用戶定義過程所產生的調用過程和 Python 中的過程類似。在一系列參數上調用過程以使用新的幀擴展當前環境，以及將過程的形參綁定到實參開始，之後在開始於新幀的環境中求出過程體的代碼行。

output的調用在 Logo 中與 Python 中的return語句有相同作用：它會中止過程體的執行，並返回一個值。Logo 過程可以通過調用stop來不帶任何值返回。

? to count
> print 1
> print 2
> stop
> print 3
> end
? count
1
2

**作用域。**Logo 是動態作用域語言。類似 Python 的詞法作用域語言並不允許一個函數的局部名稱影響另一個函數的求值，除非第二個函數顯式定義在第一個函數內。兩個頂層函數的形參完全是隔離的。在動態作用域的語言中，沒有這種隔離。當一個函數調用另一個函數時，綁定到第一個函數局部幀的名稱可在第二個函數的函數體中訪問：

? to print_last_x
> print :x
> end
? to print_x :x
> print_last_x
> end
? print_x 5
5

雖然名稱x並沒有在全局幀中綁定，而是在print_x的局部幀中，也就是首先調用的函數。Logo 的動態作用域規則允許函數print_last_x引用x，它被綁定到print_x的形式參數上。

動態作用域只需要一個對計算環境模型的簡單修改就能實現。由用戶函數調用創建的幀總是擴展自當前環境（調用處）。例如，上面的print_x調用引入了新的幀，它擴展自當前環境，當前環境中包含print_x的局部幀和全局幀。所以，在print_last_x的主體中查找x會發現局部幀中該名稱綁定到5。與之相似，在 Python 的詞法作用域下，print_last_x的幀只擴展自全局幀（定義處），而並不擴展自print_x的局部幀（調用處）。

動態作用域語言擁有一些好處，它的過程可能不需要接受許多參數。例如，print_last_x上面的過程沒有接受參數，但是它的行為仍然由內層作用域參數化。

**常規編程。**我們的 Logo 之旅就到此為止了。我們還沒有介紹任何高級特性，例如，對象系統、高階過程，或者語句。學會在 Logo 中高效編程需要將語言的簡單特性組合為有效的整體。

Logo 中沒有條件表達式類型。過程if和ifelse使用調用表達式的求值規則。if的第一個參數是個布爾單詞，True或者False。第二個參數不是輸出值，而是一個句子，包含如果第一個參數為True時需要求值的代碼行。這個設計的重要結果是，第二個函數的內容如果不被用到就不會全部求值。

? 1/0
div raised a ZeroDivisionError: division by zero
? to reciprocal :x
> if not :x = 0 [output 1 / :x]
> output "infinity
> end
? print reciprocal 2
0.5
? print reciprocal 0
infinity

Logo 的條件語句不僅僅不需要特殊語法，而且它實際上可以使用word和run實現。ifelse的基本過程接受三個函數：布爾單詞、如果單詞為True需要求值的句子，和如果單詞為False需要求值的句子。通過適當命名形式參數，我們可以實現擁有相同行為的用戶定義過程ifelse2。

? to ifelse2 :predicate :True :False
> output run run word ": :predicate
> end
? print ifelse2 emptyp [] ["empty] ["full]
empty

遞歸過程不需要任何特殊語法，它們可以和run、sentence、first和butfirst一起使用，來定義句子上的通用序列操作。例如，我們可以通過構建二元句子並執行它，來在參數上調用過程。如果參數是個單詞，它必須被引用。

? to apply_fn :fn :arg
> output run list :fn ifelse word? :arg [word "" :arg] [:arg]
> end

下面，我們可以定義一個過程，它在句子:s上逐步映射函數:fn。

? to map_fn :fn :s
> if emptyp :s [output []]
> output fput apply_fn :fn first :s map_fn :fn butfirst :s
> end
? show map "double [1 2 3]
[2 4 6]

map_fn主體的第二行也可以使用圓括號編寫，表明調用表達式的嵌套結構。但是，圓括號表示了調用表達式的開始和末尾，而不是包圍在操作數和非運算符周圍。

> (output (fput (apply_fn :fn (first :s)) (map_fn :fn (butfirst :s))))

圓括號在 Logo 中並不必須，但是它們通常幫助程序員記錄嵌套表達式的結構。許多 Lisp 的方言都需要圓括號，所以就擁有了顯式嵌套的語法。

作為最後一個例子，Logo 可以以非常緊湊的形式使用海龜製圖來遞歸作圖。謝爾賓斯基三角是個分形圖形，它繪製每個三角形的同時還繪製鄰近的三個三角形，它們的頂點是包含它們的三角形的邊上的中點。它可以由這個 Logo 程序以有限的遞歸深度來繪製。

? to triangle :exp
> repeat 3 [run :exp lt 120]
> end

? to sierpinski :d :k
> triangle [ifelse :k = 1 [fd :d] [leg :d :k]]
> end

? to leg :d :k
> sierpinski :d / 2 :k - 1
> penup fd :d pendown
> end

triangle 過程是個通用方法，它重複三次繪製過程，並在每個重複之後左轉。sierpinski 過程接受長度和遞歸深度。如果深度為1，它畫出純三角形，否則它畫出由log的調用所組成的三角形。leg過程畫出謝爾賓斯基遞歸三角型的一條邊，通過遞歸調用sierpinski 填充這條邊長度的上一半，之後將海龜移動到另一個頂點上。過程up和down通過將筆拿起並在之後放下，在海龜移動過程中停止畫圖。sierpinski和leg之間的多重遞歸產生了如下結果：

? sierpinski 400 6

3.6.3 結構

這一節描述了 Logo 解釋器的通常結構。雖然這一章是獨立的，它也確實引用了配套項目。完成這個項目會從零製造出這一章描述的解釋器的有效實現。

Logo 的解釋器可以擁有和計算器解釋器相同的結構。解析器產生表達式數據結構，它們可由求值器來解釋。求值函數檢查表達式的形式，並且對於調用表達式，它在一些參數上調用函數來應用某個過程。但是，還是存在一些結構上的不同以適應 Logo 的特殊語法。

**行。**Logo 解析器並不讀取一行代碼，而是讀取可能按序包含多個表達式的整行代碼。它不返回表達式樹，而是返回 Logo 句子。

解析器實際上只做微小的語法分析。特別是，解析工作並不會將調用表達式的運算符和操作數子表達式區分為樹的不同枝幹。反之，調用表達式的組成部分順序排列，嵌套調用表達式表示為攤平的記號序列。最終，解析工作並不判斷基本表達式，例如數值的類型，因為 Logo 沒有豐富的類型系統。反之，每個元素都是單詞或句子。

>>> parse_line('print sum 10 difference 7 3')
['print', 'sum', '10', 'difference', '7', '3']

解析器做了很微小的分析，因為 Logo 的動態特性需要求值器解析嵌套表達式的結構。

解析器並不會弄清句子的嵌套結構，句子中的句子表示為 Python 的嵌套列表。

>>> parse_line('print sentence "this [is a [deep] list]')
['print', 'sentence', '"this', ['is', 'a', ['deep'], 'list']]

parse_line的完整實現在配套項目的logo_parser.py中。

**求值。**Logo 一次求值一行。求值器的一個框架實現定義在配套項目的logo.py中。從parse_line返回的句子傳給了eval_line函數，它求出行中的每個表達式。eval_line函數重複調用logo_eval，它求出行中的下一個完整的表達式，直到這一行全部求值完畢，之後返回最後一個值。logo_eval函數求出單個表達式。

logo_eval函數求出不同形式的表達式：基本、變量、定義、引用和調用表達式，我們已經在上一節中介紹過它們了。Logo 中多元素表達式的形式可以由檢查第一個元素來判斷。表達式的每個形式都有自己的求值規則。

1. 基本表達式（可以解釋為數值、True或False的單詞）求值為自身。
2. 變量在環境中查找。環境會在下一節中詳細討論。
3. 定義處理為特殊情況。用戶定義過程也在下一節中詳細討論。
4. 引用表達式求值為引用的文本，它是個去掉前導引號的字符串。句子（表示為 Python 列表）也看做引用，它們求值為自身。
5. 調用表達式在當前環境中查找運算符名稱，並且調用綁定到該名稱的過程。

下面是logo_apply的簡單實現。我們去掉了一些錯誤檢查，以專注於我們的討論。配套項目中有更加健壯的實現。

>>> def logo_eval(line, env):
        """Evaluate the first expression in a line."""
        token = line.pop()
        if isprimitive(token):
            return token
        elif isvariable(token):
            return env.lookup_variable(variable_name(token))
        elif isdefinition(token):
            return eval_definition(line, env)
        elif isquoted(token):
            return text_of_quotation(token)
        else:
            procedure = env.procedures.get(token, None)
            return apply_procedure(procedure, line, env)

上面的最後情況調用了第二個過程，表達為函數apply_procedure。為了調用由運算符記號命名的過程，這個運算符會在當前環境中查找。在上面的定義中，env是Environment 類的實例，會在下一節中描述。env.procedures屬性是個儲存運算符名稱和過程之間映射的字典。在 Logo 中，環境擁有單詞的這種映射，並且沒有局部定義的過程。而且，Logo 為過程名稱和變量名稱維護分離的映射，叫做分離的命名空間。但是，以這種方式複用名稱並不推薦。

**過程調用。**過程調用以調用apply_procedure函數開始，它被傳入由logo_apply查找到的函數，並帶有代碼的當前行和當前環境。Logo 中過程調用的過程比計算器中的calc_apply更加通用。特別是，apply_procedure必須檢查打算調用的過程，以便在求解n個運算符表達式之前，判斷它的參數數量n。這裡我們會看到，為什麼 Logo 解析器不能僅僅由語法分析構建表達式樹，因為樹的結構由過程決定。

apply_procedure函數調用collect_args 函數，它必須重複調用logo_eval來求解行中的下n個表達式。之後，計算完過程的參數之後，apply_procedure調用了logo_apply，實際上這個函數在參數上調用過程。下面的調用圖示展示了這個過程。

最終的函數 logo_apply接受兩種參數：基本過程和用戶定義的過程，二者都是Procedure的實例。Procedure是一個 Python 對象，它擁有過程的名稱、參數數量、主體和形式參數作為實例屬性。body屬性可以擁有不同類型。基本過程在 Python 中已經實現，所以它的body就是 Python 函數。用戶定義的過程（非基本）定義在 Logo 中，所以它的 body就是 Logo 代碼行的列表。Procedure也擁有兩個布爾值屬性。一個用於表明是否是基本過程，另一個用於表明是否需要訪問當前環境。

>>> class Procedure():
        def __init__(self, name, arg_count, body, isprimitive=False,
                     needs_env=False, formal_params=None):
            self.name = name
            self.arg_count = arg_count
            self.body = body
            self.isprimitive = isprimitive
            self.needs_env = needs_env
            self.formal_params = formal_params

基本過程通過在參數列表上調用主體，並返回它的返回值作為過程輸出來應用。

>>> def logo_apply(proc, args):
        """Apply a Logo procedure to a list of arguments."""
        if proc.isprimitive:
            return proc.body(*args)
        else:
            """Apply a user-defined procedure"""

用戶定義過程的主體是代碼行的列表，每一行都是 Logo 句子。為了在參數列表上調用過程，我們在新的環境中求出主體的代碼行。為了構造這個環境，我們向當前環境中添加新的幀，過程的形式參數在裡面綁定到實參上。這個過程的重要結構化抽象是，求出用戶定義過程的主體的代碼行，需要遞歸調用eval_line。

**求值/應用遞歸。**實現求值過程的函數，eval_line 和logo_eval，以及實現函數應用過程的函數，apply_procedure、collect_args和logo_apply，是互相遞歸的。無論何時調用表達式被發現，求值操作都需要調用它。應用操作使用求值來求出實參中的操作數表達式，以及求出用戶定義過程的主體。這個互相遞歸過程的通用結構在解釋器中非常常見：求值以應用定義，應用又使用求值定義。

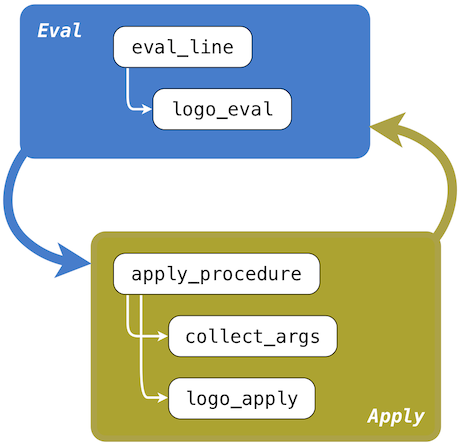
這個遞歸循環終止於語言的基本類型。求值的基本條件是，求解基本表達式、變量、引用表達式或定義。函數調用的基本條件是調用基本過程。這個互相遞歸的結構，在處理表達式形式的求值函數，和處理函數及其參數的應用之間，構成了求值過程的本質。

3.6.4 環境

既然我們已經描述了 Logo 解釋器的結構，我們轉而實現Environment 類，便於讓它使用動態作用域正確支持賦值、過程定義和變量查找。Environment實例表示名稱綁定的共有集合，可以在程序執行期間的某一點上訪問。綁定在幀中組織，而幀以 Python 字典實現。幀包含變量的名稱綁定，但不包含過程。運算符名稱和Procedure實例之間的綁定在 Logo 中是單獨儲存的。在這個實現中，包含變量名稱綁定的幀儲存為字典的列表，位於Environment的_frames屬性中，而過程名稱綁定儲存在值為字典的procedures屬性中。

幀不能直接訪問，而是通過兩個Environment的方法：lookup_variable和set_variable_value。前者實現了一個過程，與我們在第一章的計算環境模型中引入的查找過程相同。名稱在當前環境第一幀（最新添加）中與值匹配。如果它被找到，所綁定的值會被返回。如果沒有找到，會在被當前幀擴展的幀中尋找。

set_variable_value 也會尋找與變量名稱匹配的綁定。如果找到了，它會更新為新的值，如果沒有找到，那麼會在全局幀上創建新的綁定。這些方法的實現留做配套項目中的練習。

lookup_variable 方法在求解變量名稱時由logo_eval調用。set_variable_value 由logo_make函數調用，它用作 Logo 中make基本過程的主體。

除了變量和make基本過程之外，我們的解釋器支持它的第一種抽象手段：將名稱綁定到值上。在 Logo 中，我們現在可以重複我們第一章中的第一種抽象步驟。

? make "radius 10
? print 2 * :radius
20

賦值只是抽象的一種有限形式。我們已經從這門課的開始看到，即使對於不是很大的程序，用戶定義函數也是管理複雜性的關鍵工具。我們需要兩個改進來實現 Logo 中的用戶定義過程。首先，我們必須描述eval_definition的實現，如果當前行是定義，logo_eval會調用這個 Python 函數。其次，我們需要在logo_apply中完成我們的描述，它在一些參數上調用用戶過程。這兩個改動都需要利用上一節定義的Procedure類。

定義通過創建新的Procedure實例來求值，它表示用戶定義的過程。考慮下面的 Logo 過程定義：

? to factorial :n
> output ifelse :n = 1 [1] [:n * factorial :n - 1]
> end
? print fact 5
120

定義的第一行提供了過程的名稱factorial和形參n。隨後的一些行組成了過程體。這些行並不會立即求值，而是為將來使用而儲存。也就是說，這些行由eval_definition讀取並解析，但是並不傳遞給eval_line。主體中的行一直讀取，直到出現了只包含end的行。在 Logo 中，end並不是需要求值的過程，也不是過程體的一部分。它是個函數定義末尾的語法標記。

Procedure實例從這個過程的名稱、形參列表以及主體中創建，並且在環境中的procedures的字典屬性中註冊。不像 Python，在 Logo 中，一旦過程綁定到一個名稱，其它定義都不能複用這個名稱。

logo_apply將Procedure實例應用於一些參數，它是表示為字符串的 Logo 值（對於單詞），或列表（對於句子）。對於用戶定義過程，logo_apply創建了新的幀，它是一個字典對象，鍵是過程的形參，值是實參。在動態作用域語言例如 Logo 中，這個新的幀總是擴展自過程調用處的當前環境。所以，我們將新創建的幀附加到當前環境上。之後，主體中的每一行都依次傳遞給eval_line 。最後，在主體完成求值後，我們可以從環境中移除新創建的幀。由於 Logo 並不支持高階或一等過程，在程序執行期間，我們並不需要一次跟蹤多於一個環境。

下面的例子演示了幀的列表和動態作用域規則，它們由調用這兩個 Logo 用戶定義過程產生：

? to f :x
> make "z sum :x :y
> end
? to g :x :y
> f sum :x :x
> end
? g 3 7
? print :z
13

由這些表達式的求值創建的環境分為過程和幀，它們維護在分離的命名空間中。幀的順序由調用順序決定。

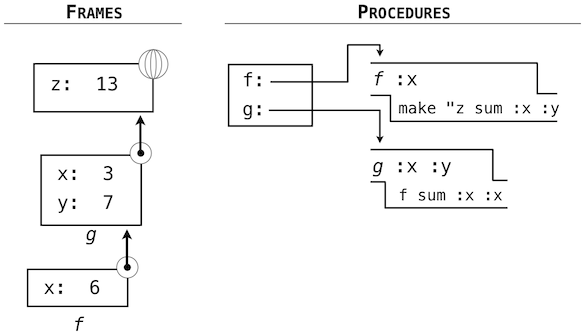
3.6.5 數據即程序

在思考求值 Logo 表達式的程序時，一個類比可能很有幫助。程序含義的一個可取觀點是，程序是抽象機器的描述。例如，再次思考下面的計算階乘的過程：

? to factorial :n
> output ifelse :n = 1 [1] [:n * factorial :n - 1]
> end

我們可以在 Python 中表達為等價的程序，使用傳統的表達式。

>>> def factorial(n):
        return 1 if n == 1 else n * factorial(n - 1)

我們可能將這個程序看做機器的描述，它包含幾個部分，減法、乘法和相等性測試，並帶有兩相開關和另一個階乘機器（階乘機器是無限的，因為它在其中包含另一個階乘機器）。下面的圖示是一個階乘機器的流程圖，展示了這些部分是怎麼組合到一起的。

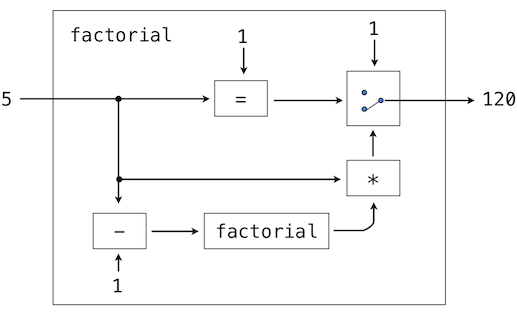
與之相似，我們可以將 Logo 解釋器看做非常特殊的機器，它接受機器的描述作為輸入。給定這個輸入，解釋器就能配置自己來模擬描述的機器。例如，如果我們向解釋器中輸入階乘的定義，解釋器就可以計算階乘。

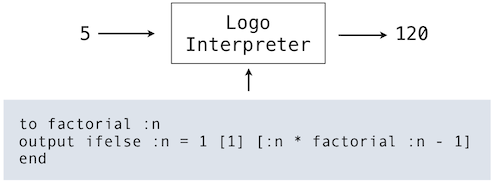
從這個觀點得出，我們的 Logo 解釋器可以看做通用的機器。當輸入以 Logo 程序描述時，它就能模擬其它機器。它在由我們的編程語言操作的數據對象，和編程語言自身之間起到銜接作用。想象一下，一個用戶在我們正在運行的 Logo 解釋器中輸入了 Logo 表達式。從用戶的角度來看，類似sum 2 2的輸入表達式是編程語言中的表達式，解釋器應該對其求值。但是，從解釋器的角度來看，表達式只是單詞組成的句子，可以根據定義好的一系列規則來操作它。

用戶的程序是解釋器的數據，這不應該是混亂的原因。實際上，有時候忽略這個差異會更方便，以及讓用戶能夠顯式將數據對象求值為表達式。在 Logo 中，無論我們何時使用run 過程，我們都使用了這種能力。Python 中也存在相似的函數：eval函數會求出 Python 表達式，exec函數會求出 Python 語句，所以：

>>> eval('2+2')
4

和

>>> 2+2
4

返回了相同的結果。求解構造為指令的一部分的表達式是動態編程語言的常見和強大的特性。這個特性在 Logo 中十分普遍，很少語言是這樣，但是在程序執行期間構造和求解表達式的能力，對任何程序員來說都是有價值的工具。

第四章 分佈式和並行計算

來源：Chapter 4: Distributed and Parallel Computing

譯者：飛龍

協議：CC BY-NC-SA 4.0

4.1 引言

目前為止，我們專注於如何創建、解釋和執行程序。在第一章中，我們學會使用函數作為組合和抽象的手段。第二章展示瞭如何使用數據結構和對象來表示和操作數據，以及向我們介紹了數據抽象的概念。在第三章中，我們學到了計算機程序如何解釋和執行。結果是，我們理解了如何設計程序，它們在單一處理器上運行。

這一章中，我們跳轉到協調多個計算機和處理器的問題。首先，我們會觀察分佈式系統。它們是互相連接的獨立計算機，需要互相溝通來完成任務。它們可能需要協作來提供服務，共享數據，或者甚至是儲存太大而不能在一臺機器上裝下的數據。我們會看到，計算機可以在分佈式系統中起到不同作用，並且瞭解各種信息，計算機需要交換它們來共同工作。

接下來，我們會考慮並行計算。並行計算是這樣，當一個小程序由多個處理器使用共享內存執行時，所有處理器都並行工作來使任務完成得更快。併發（或並行）引入了新的挑戰，並且我們會開發新的機制來管理併發程序的複雜性。

4.2 分佈式系統

分佈式系統是自主的計算機網絡，計算機互相通信來完成一個目標。分佈式系統中的計算機都是獨立的，並且沒有物理上共享的內存或處理器。它們使用消息來和其它計算機通信，消息是網絡上從一臺計算機到另一臺計算機傳輸的一段信息。消息可以用於溝通許多事情：計算機可以讓其它計算機來執行一個帶有特定參數的過程，它們可以發送和接受數據包，或者發送信號讓其它計算機執行特定行為。

分佈式系統中的計算機具有不同的作用。計算機的作用取決於系統的目標，以及計算機自身的硬件和軟件屬性。分佈式系統中，有兩種主要方式來組織計算機，一種叫客戶端-服務端架構（C/S 架構），另一種叫做對等網絡架構（P2P 架構）。

4.2.1 C/S 系統

C/S 架構是一種從中心來源分發服務的方式。只有單個服務端提供服務，多臺客戶端和服務器通信來消耗它的產出。在這個架構中，客戶端和服務端都有不同的任務。服務端的任務就是響應來自客戶端的服務請求，而客戶端的任務就是使用響應中提供的數據來執行一些任務。

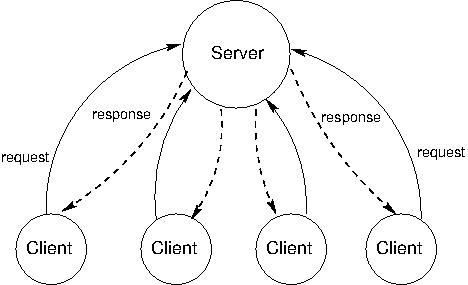
C/S 通信模型可以追溯到二十世紀七十年代 Unix 的引入，但這一模型由於現代萬維網（WWW）中的使用而變得具有影響力。一個C/S 交互的例子就是在線閱讀紐約時報。當www.nytimes.com上的服務器與瀏覽器客戶端（比如 Firefox）通信時，它的任務就是發送回來紐約時報主頁的 HTML。這可能涉及到基於發送給服務器的用戶賬戶信息，計算個性化的內容。這意味著需要展示圖片，安排視覺上的內容，展示不同的顏色、字體和圖形，以及允許用戶和渲染後的頁面交互。

客戶端和服務端的概念是強大的函數式抽象。服務端僅僅是一個提供服務的單位，可能同時對應多個客戶端。客戶端是消耗服務的單位。客戶端並不需要知道服務如何提供的細節，或者所獲取的數據如何儲存和計算，服務端也不需要知道數據如何使用。

在網絡上，我們認為客戶端和服務端都是不同的機器，但是，一個機器上的系統也可以擁有 C/S 架構。例如，來自計算機輸入設備的信號需要讓運行在計算機上的程序來訪問。這些程序就是客戶端，消耗鼠標和鍵盤的輸入數據。操作系統的設備驅動就是服務端，接受物理的信號並將它們提供為可用的輸入。

C/S 系統的一個缺陷就是，服務端是故障單點。它是唯一能夠分發服務的組件。客戶端的數量可以是任意的，它們可以交替，並且可以按需出現和消失。但是如果服務器崩潰了，整個系統就會停止工作。所以，由 C/S 架構創建的函數式抽象也使它具有崩潰的風險。

C/S 系統的另一個缺陷是，當客戶端非常多的時候，資源就變得稀缺。客戶端增加系統上的命令而不貢獻任何計算資源。C/S 系統不能隨著不斷變化的需求縮小或擴大。

4.2.2 P2P 系統

C/S 模型適合於服務導向的情形。但是，還有其它計算目標，適合使用更加平等的分工。P2P 的術語用於描述一種分佈式系統，其中勞動力分佈在系統的所有組件中。所有計算機發送並接受數據，它們都貢獻一些處理能力和內存。隨著分佈式系統的規模增長，它的資源計算能力也會增長。在 P2P 系統中，系統的所有組件都對分佈式計算貢獻了一些處理能力和內存。

所有參與者的勞動力的分工是 P2P 系統的識別特徵。也就是說，對等者需要能夠和其它人可靠地通信。為了確保消息到達預定的目的地，P2P 系統需要具有組織良好的網絡結構。這些系統中的組件協作來維護足夠的其它組件的位置信息並將消息發送到預定的目的地。

在一些 P2P 系統中，維護網絡健康的任務由一系列特殊的組件執行。這種系統並不是純粹的 P2P 系統，因為它們具有不同類型的組件類型，提供不同的功能。支持 P2P 網絡的組件就像腳手架那樣：它們有助於網絡保持連接，它們維護不同計算機的位置信息，並且它們新來者來鄰居中找到位置。

P2P 系統的最常見應用就是數據傳送和存儲。對於數據傳送，系統中的每臺計算機都致力於網絡上的數據傳送。如果目標計算機是特定計算機的鄰居，那臺計算機就一起幫助傳送數據。對於數據存儲，數據集可以過於龐大，不能在任何單臺計算機內裝下，或者儲存在單臺計算機內具有風險。每臺計算機都儲存數據的一小部分，不同的計算機上可能會儲存相同數據的多個副本。當一臺計算機崩潰時，上面的數據可以由其它副本恢復，或者在更換替代品之後放回。

Skype，一個音頻和視頻聊天服務，是採用 P2P 架構的數據傳送應用的示例。當不同計算機上的兩個人都使用 Skype 交談時，它們的通信會拆成由 1 和 0 構成的數據包，並且通過 P2P 網絡傳播。這個網絡由電腦上註冊了 Skype 的其它人組成。每臺計算機都知道附近其它人的位置。一臺計算機通過將數據包傳給它的鄰居，來幫助將它傳到目的地，它的鄰居又將它傳給其它鄰居，以此類推，直到數據包到達了它預定的目的地。Skype 並不是純粹的 P2P 系統。一個超級節點組成的腳手架網絡用於用戶登錄和退出，維護它們的計算機的位置信息，並且修改網絡結構來處理用戶進入和離開。

4.2.3 模塊化

我們剛才考慮的兩個架構 -- P2P 和 C/S -- 都為強制模塊化而設計。模塊化是一個概念，系統的組件對其它組件來說應該是個黑盒。組件如何實現行為應該並不重要，只要它提供了一個接口：規定了輸入應該產生什麼輸出。

在第二章中，我們在調度函數和麵向對象編程的上下文中遇到了接口。這裡，接口的形式為指定對象應接收的信息，以及對象應如何響應它們。例如，為了提供“表示為字符串”的接口，對象必須回覆__repr__和__str__信息，並且在響應中輸出合適的字符串。那些字符串的生成如何實現並不是接口的一部分。

在分佈式系統中，我們必須考慮涉及到多臺計算機的程序設計，所以我們將接口的概念從對象和消息擴展為整個程序。接口指定了應該接受的輸入，以及應該在響應中返回給輸入的輸出。

接口在真實世界的任何地方都存在，我們經常習以為常。一個熟悉的例子就是 TV 遙控器。你可以買到許多牌子的遙控器或者 TV，它們都能工作。它們的唯一共同點就是“TV 遙控器”的接口。只要當你按下電院、音量、頻道或者其它任何按鈕（輸入）時，一塊電路向你的 TV 發送正確的信號（輸出），它就遵循“TV 遙控器”接口。

模塊化給予系統許多好處，並且是一種沉思熟慮的系統設計。首先，模塊化的系統易於理解。這使它易於修改和擴展。其次，如果系統中什麼地方發生錯誤，只需要更換有錯誤的組件。再者，bug 或故障可以輕易定位。如果組件的輸出不符合接口的規定，而且輸入是正確的，那麼這個組件就是故障來源。

4.2.4 消息傳遞

在分佈式系統中，組件使用消息傳遞來互相溝通。消息有三個必要部分：發送者、接收者和內容。發送者需要被指定，便於接受者得知哪個組件發送了信息，以及將回復發送到哪裡。接收者需要被指定，便於任何協助發送消息的計算機知道發送到哪裡。消息的內容是最寶貴的。取決於整個系統的函數，內容可以是一段數據、一個信號，或者一條指令，讓遠程計算機來以一些參數求出某個函數。

消息傳遞的概念和第二章的消息傳遞機制有很大關係，其中，調度函數或字典會響應值為字符串的信息。在程序中，發送者和接受者都由求值規則標識。但是在分佈式系統中，接受者和發送者都必須顯式編碼進消息中。在程序中，使用字符串來控制調度函數的行為十分方便。在分佈式系統中，消息需要經過網絡發送，並且可能需要存放許多不同種類的信號作為“數據”，所以它們並不始終編碼為字符串。但是在兩種情況中，消息都服務於相同的函數。不同的組件（調度函數或計算機）交換消息來完成一個目標，它需要多個組件模塊的協作。

在較高層面上，消息內容可以是複雜的數據結構，但是在較低層面上，消息只是簡單的 1 和 0 的流，在網絡上傳輸。為了變得易用，所有網絡上發送的消息都需要根據一致的消息協議格式化。

消息協議是一系列規則，用於編碼和解碼消息。許多消息協議規定，消息必須符合特定的格式，其中特定的比特具有固定的含義。固定的格式實現了固定的編碼和解碼規則來生成和讀取這種格式。分佈式系統中的所有組件都必須理解協議來互相通信。這樣，它們就知道消息的哪個部分對應哪個信息。

消息協議並不是特定的程序或軟件庫。反之，它們是可以由大量程序使用的規則，甚至以不同的編程語言編寫。所以，帶有大量不同軟件系統的計算機可以加入相同的分佈式系統，只需要遵守控制這個系統的消息協議。

4.2.5 萬維網上的消息

HTTP（超文本傳輸協議的縮寫）是萬維網所支持的消息協議。它指定了在 Web 瀏覽器和服務器之間交換的消息格式。所有 Web 瀏覽器都使用 HTTP 協議來請求服務器上的頁面，而且所有 Web 服務器都使用 HTTP 格式來發回它們的響應。

當你在 Web 瀏覽器上鍵入 URL 時，比如 http://en.wikipedia.org/wiki/UC_Berkeley，你實際上就告訴了你的計算機，使用 "HTTP" 協議，從 "http://en.wikipedia.org/wiki/UC_Berkeley" 的服務器上請求 "wiki/UC_Berkeley" 頁面。消息的發送者是你的計算機，接受者是 en.wikipedia.org，以及消息內容的格式是：

GET /wiki/UC_Berkeley HTTP/1.1

第一個單詞是請求類型，下一個單詞是所請求的資源，之後是協議名稱（HTTP）和版本（1.1）。（請求還有其它類型，例如 PUT、POST 和 HEAD，Web 瀏覽器也會使用它們。）

服務器發回了回覆。這時，發送者是 en.wikipedia.org，接受者是你的計算機，消息內容的格式是由數據跟隨的協議頭：

HTTP/1.1 200 OK
Date: Mon, 23 May 2011 22:38:34 GMT
Server: Apache/1.3.3.7 (Unix) (Red-Hat/Linux)
Last-Modified: Wed, 08 Jan 2011 23:11:55 GMT
Content-Type: text/html; charset=UTF-8

... web page content ...

第一行，單詞 "200 OK" 表示沒有發生錯誤。協議頭下面的行提供了有關服務器的信息，日期和發回的內容類型。協議頭和頁面的實際內容通過一個空行來分隔。

如果你鍵入了錯誤的 Web 地址，或者點擊了死鏈，你可能會看到類似於這個錯誤的消息：

404 Error File Not Found

它的意思是服務器發送回了一個 HTTP 協議頭，以這樣起始：

HTTP/1.1 404 Not Found

一系列固定的響應代碼是消息協議的普遍特性。協議的設計者試圖預料通過協議發送的常用消息，並且賦為固定的代碼來減少傳送大小，以及建立通用的消息語義。在 HTTP 協議中，200 響應代碼表示成功，而 404 表示資源沒有找到的錯誤。其它大量響應代碼也存在於 HTTP 1.1 標準中。

HTTP 是用於通信的固定格式，但是它允許傳輸任意的 Web 頁面。其它互聯網上的類似協議是 XMPP，即時消息的常用協議，以及 FTP，用於在客戶端和服務器之間下載和上傳文件的協議。

4.3 並行計算

計算機每一年都會變得越來越快。在 1965 年，英特爾聯合創始人戈登·摩爾預測了計算機將如何隨時間而變得越來越快。僅僅基於五個數據點，他推測，一個芯片中的晶體管數量每兩年將翻一倍。近50年後，他的預測仍驚人地準確，現在稱為摩爾定律。

儘管速度在爆炸式增長，計算機還是無法跟上可用數據的規模。根據一些估計，基因測序技術的進步將使可用的基因序列數據比處理器變得更快的速度還要快。換句話說，對於遺傳數據，計算機變得越來越不能處理每年需要處理的問題規模，即使計算機本身變得越來越快。

為了規避對單個處理器速度的物理和機械約束，製造商正在轉向另一種解決方案：多處理器。如果兩個，或三個，或更多的處理器是可用的，那麼許多程序可以更快地執行。當一個處理器在做一些計算的一個切面時，其他的可以在另一個切面工作。所有處理器都可以共享相同的數據，但工作並行執行。

為了能夠合作，多個處理器需要能夠彼此共享信息。這通過使用共享內存環境來完成。該環境中的變量、對象和數據結構對所有的進程可見。處理器在計算中的作用是執行編程語言的求值和執行規則。在一個共享內存模型中，不同的進程可能執行不同的語句，但任何語句都會影響共享環境。

4.3.1 共享狀態的問題

多個進程之間的共享狀態具有單一進程環境沒有的問題。要理解其原因，讓我們看看下面的簡單計算：

x = 5
x = square(x)
x = x + 1

x的值是隨時間變化的。起初它是 5，一段時間後它是 25，最後它是 26。在單一處理器的環境中，沒有時間依賴性的問題。x的值在結束時總是 26。但是如果存在多個進程，就不能這樣說了。假設我們並行執行了上面代碼的最後兩行：一個處理器執行x = square(x)而另一個執行x = x + 1。每一個這些賦值語句都包含查找當前綁定到x的值，然後使用新值更新綁定。讓我們假設x是共享的，同一時間只有一個進程讀取或寫入。即使如此，讀和寫的順序可能會有所不同。例如，下面的例子顯示了兩個進程的每個進程的一系列步驟，P1和P2。每一步都是簡要描述的求值過程的一部分，隨時間從上到下執行：

P1                    P2
read x: 5
                      read x: 5
calculate 5*5: 25     calculate 5+1: 6
write 25 -> x
                      write x-> 6

在這個順序中，x的最終值為 6。如果我們不協調這兩個過程，我們可以得到另一個順序的不同結果：

P1                    P2
                      read x: 5
read x: 5             calculate 5+1: 6
calculate 5*5: 25     write x->6
write 25 -> x

在這個順序中，x將是 25。事實上存在多種可能性，這取決於進程執行代碼行的順序。x的最終值可能最終為 5，25，或預期值 26。

前面的例子是無價值的。square(x)和x = x + 1是簡單快速的計算。我們強迫一條語句跑在另一條的後面，並不會失去太多的時間。但是什麼樣的情況下，並行化是必不可少的？這種情況的一個例子是銀行業。在任何給定的時間，可能有成千上萬的人想用他們的銀行賬戶進行交易：他們可能想在商店刷卡，存入支票，轉帳，或支付賬單。即使一個帳戶在同一時間也可能有活躍的多個交易。

讓我們看看第二章的make_withdraw函數，下面是修改過的版本，在更新餘額之後打印而不是返回它。我們感興趣的是這個函數將如何併發執行。

>>> def make_withdraw(balance):
        def withdraw(amount):
            nonlocal balance
            if amount > balance:
                print('Insufficient funds')
            else:
                balance = balance - amount
                print(balance)
        return withdraw

現在想象一下，我們以 10 美元創建一個帳戶，讓我們想想，如果我們從帳戶中提取太多的錢會發生什麼。如果我們順序執行這些交易，我們會收到資金不足的消息。

>>> w = make_withdraw(10)
>>> w(8)
2
>>> w(7)
'Insufficient funds'

但是，在並行中可以有許多不同的結果。下面展示了一種可能性：

P1: w(8)                        P2: w(7)
read balance: 10
read amount: 8                  read balance: 10
8 > 10: False                   read amount: 7
if False                        7 > 10: False
10 - 8: 2                       if False
write balance -> 2              10 - 7: 3
read balance: 2                 write balance -> 3
print 2                         read balance: 3
                                print 3

這個特殊的例子給出了一個不正確結果 3。就好像w(8)交易從來沒有發生過。其他可能的結果是 2，和'Insufficient funds'。這個問題的根源是：如果P2 在P1寫入值前讀取餘額，P2的狀態是不一致的（反之亦然）。P2所讀取的餘額值是過時的，因為P1打算改變它。P2不知道，並且會用不一致的值覆蓋它。

這個例子表明，並行化的代碼不像把代碼行分給多個處理器來執行那樣容易。變量讀寫的順序相當重要。

一個保證執行正確性的有吸引力的方式是，兩個修改共享數據的程序不能同時執行。不幸的是，對於銀行業這將意味著，一次只可以進行一個交易，因為所有的交易都修改共享數據。直觀地說，我們明白，讓 2 個不同的人同時進行完全獨立的帳戶交易應該沒有問題。不知何故，這兩個操作不互相干擾，但在同一帳戶上的相同方式的同時操作就相互干擾。此外，當進程不讀取或寫入時，讓它們同時運行就沒有問題。

4.3.2 並行計算的正確性

並行計算環境中的正確性有兩個標準。第一個是，結果應該總是相同。第二個是，結果應該和串行執行的結果一致。

第一個條件表明，我們必須避免在前面的章節中所示的變化，其中在不同的方式下的交叉讀寫會產生不同的結果。例子中，我們從 10 美元的帳戶取出了w(8)和w(7)。這個條件表明，我們必須始終返回相同的答案，獨立於P1和P2的指令執行順序。無論如何，我們必須以這樣一種方式來編寫我們的程序，無論他們如何相互交叉，他們應該總是產生同樣的結果。

第二個條件揭示了許多可能的結果中哪個是正確的。例子中，我們從 10 美元的帳戶取出了w(8)和w(7)，這個條件表明結果必須總是餘額不足，而不是 2 或者 3。

當一個進程在程序的臨界區影響另一個進程時，並行計算中就會出現問題。這些都是需要執行的代碼部分，它們看似是單一的指令，但實際上由較小的語句組成。一個程序會以一系列原子硬件指令執行，由於處理器的設計，這些是不能被打斷或分割為更小單元的指令。為了在並行的情況下表現正確，程序代碼的臨界區需要具有原子性，保證他們不會被任何其他代碼中斷。

為了強制程序臨界區在併發下的原子性，需要能夠在重要的時刻將進程序列化或彼此同步。序列化意味著同一時間只運行一個進程 -- 這一瞬間就好像串行執行一樣。同步有兩種形式。首先是互斥，進程輪流訪問一個變量。其次是條件同步，在滿足條件（例如其他進程完成了它們的任務）之前進程一直等待，之後繼續執行。這樣，當一個程序即將進入臨界區時，其他進程可以一直等待到它完成，然後安全地執行。

4.3.3 保護共享狀態：鎖和信號量

在本節中討論的所有同步和序列化方法都使用相同的基本思想。它們在共享狀態中將變量用作信號，所有過程都會理解並遵守它。這是一個相同的理念，允許分佈式系統中的計算機協同工作 -- 它們通過傳遞消息相互協調，根據每一個參與者都理解和遵守的一個協議。

這些機制不是為了保護共享狀態而出現的物理障礙。相反，他們是建立相互理解的基礎上。和出現在十字路口的各種方向的車輛能夠安全通行一樣，是同一種相互理解。這裡沒有物理的牆壁阻止汽車相撞，只有遵守規則，紅色意味著“停止”，綠色意味著“通行”。同樣，沒有什麼可以保護這些共享變量，除非當一個特定的信號表明輪到某個進程了，進程才會訪問它們。

**鎖。**鎖，也被稱為互斥體（mutex），是共享對象，常用於發射共享狀態被讀取或修改的信號。不同的編程語言實現鎖的方式不同，但是在 Python 中，一個進程可以調用acquire()方法來嘗試獲得鎖的“所有權”，然後在使用完共享變量的時候調用release()釋放它。當進程獲得了一把鎖，任何試圖執行acquire()操作的其他進程都會自動等待到鎖被釋放。這樣，同一時間只有一個進程可以獲得一把鎖。

對於一把保護一組特定的變量的鎖，所有的進程都需要編程來遵循一個規則：一個進程不擁有特定的鎖就不能訪問相應的變量。實際上，所有進程都需要在鎖的acquire()和release()語句之間“包裝”自己對共享變量的操作。

我們可以把這個概念用於銀行餘額的例子中。該示例的臨界區是從餘額讀取到寫入的一組操作。我們看到，如果一個以上的進程同時執行這個區域，問題就會發生。為了保護臨界區，我們需要使用一把鎖。我們把這把鎖稱為balance_lock（雖然我們可以命名為任何我們喜歡的名字）。為了鎖定實際保護的部分，我們必須確保試圖進入這部分時調用acquire()獲取鎖，以及之後調用release()釋放鎖，這樣可以輪到別人。

>>> from threading import Lock
>>> def make_withdraw(balance):
        balance_lock = Lock()
        def withdraw(amount):
            nonlocal balance
            # try to acquire the lock
            balance_lock.acquire()
            # once successful, enter the critical section
            if amount > balance:
                print("Insufficient funds")
            else:
                balance = balance - amount
                print(balance)
            # upon exiting the critical section, release the lock
            balance_lock.release()

如果我們建立和之前一樣的情形：

w = make_withdraw(10)

現在就可以並行執行w(8)和w(7)了：

P1                                  P2
acquire balance_lock: ok
read balance: 10                    acquire balance_lock: wait
read amount: 8                      wait
8 > 10: False                       wait
if False                            wait
10 - 8: 2                           wait
write balance -> 2                  wait
read balance: 2                     wait
print 2                             wait
release balance_lock                wait
                                    acquire balance_lock:ok
                                    read balance: 2
                                    read amount: 7
                                    7 > 2: True
                                    if True
                                    print 'Insufficient funds'
                                    release balance_lock

我們看到了，兩個進程同時進入臨界區是可能的。某個進程實例獲取到了balance_lock，另一個就得等待，直到那個進程退出了臨界區，它才能開始執行。

要注意程序不會自己終止，除非P1釋放了balance_lock。如果它沒有釋放balance_lock，P2永遠不可能獲取它，而是一直會等待。忘記釋放獲得的鎖是並行編程中的一個常見錯誤。

**信號量。**信號量是用於維持有限資源訪問的信號。它們和鎖類似，除了它們可以允許某個限制下的多個訪問。它就像電梯一樣只能夠容納幾個人。一旦達到了限制，想要使用資源的進程就必須等待。其它進程釋放了信號量之後，它才可以獲得。

例如，假設有許多進程需要讀取中心數據庫服務器的數據。如果過多的進程同時訪問它，它就會崩潰，所以限制連接數量就是個好主意。如果數據庫只能同時支持N=2的連接，我們就可以以初始值N=2來創建信號量。

>>> from threading import Semaphore
>>> db_semaphore = Semaphore(2) # set up the semaphore
>>> database = []
>>> def insert(data):
        db_semaphore.acquire() # try to acquire the semaphore
        database.append(data)  # if successful, proceed
        db_semaphore.release() # release the semaphore
>>> insert(7)
>>> insert(8)
>>> insert(9)

信號量的工作機制是，所有進程只在獲取了信號量之後才可以訪問數據庫。只有N=2個進程可以獲取信號量，其它的進程都需要等到其中一個進程釋放了信號量，之後在訪問數據庫之前嘗試獲取它。

P1                          P2                           P3
acquire db_semaphore: ok    acquire db_semaphore: wait   acquire db_semaphore: ok
read data: 7                wait                         read data: 9
append 7 to database        wait                         append 9 to database
release db_semaphore: ok    acquire db_semaphore: ok     release db_semaphore: ok
                            read data: 8
                            append 8 to database
                            release db_semaphore: ok

值為 1 的信號量的行為和鎖一樣。

4.3.4 保持同步：條件變量

條件變量在並行計算由一系列步驟組成時非常有用。進程可以使用條件變量，來用信號告知它完成了特定的步驟。之後，等待信號的其它進程就會開始它們的任務。一個需要逐步計算的例子就是大規模向量序列的計算。在計算生物學，Web 範圍的計算，和圖像處理及圖形學中，常常需要處理非常大型（百萬級元素）的向量和矩陣。想象下面的計算：

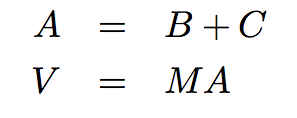
我們可以通過將矩陣和向量按行拆分，並把每一行分配到單獨的線程上，來並行處理每一步。作為上面的計算的一個實例，想象下面的簡單值：

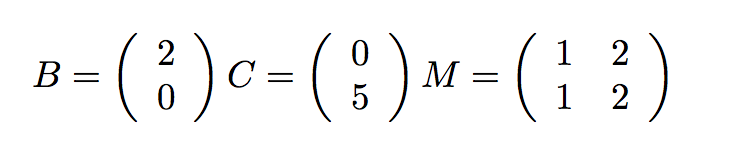
我們將前一半（這裡是第一行）分配給一個線程，後一半（第二行）分配給另一個線程：

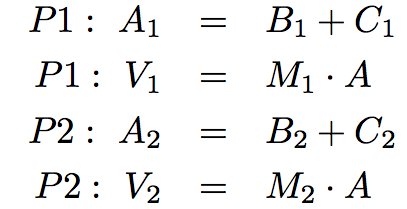
在偽代碼中，計算是這樣的：

def do_step_1(index):
  A[index] = B[index] + C[index]

def do_step_2(index):
        V[index] = M[index] . A

進程 1 執行了：

do_step_1(1)
do_step_2(1)

進程 2 執行了：

do_step_1(2)
do_step_2(2)

如果允許不帶同步處理，就造成下面的不一致性：

P1                          P2
read B1: 2
read C1: 0
calculate 2+0: 2
write 2 -> A1               read B2: 0
read M1: (1 2)              read C2: 5
read A: (2 0)               calculate 5+0: 5
calculate (1 2).(2 0): 2    write 5 -> A2
write 2 -> V1               read M2: (1 2)
                            read A: (2 5)
                            calculate (1 2).(2 5):12
                            write 12 -> V2

問題就是V直到所有元素計算出來時才會計算出來。但是，P1在A的所有元素計算出來之前，完成A = B+C並且移到V = MA。所以它與M相乘時使用了A的不一致的值。

我們可以使用條件變量來解決這個問題。

條件變量是表現為信號的對象，信號表示某個條件被滿足。它們通常被用於協調進程，這些進程需要在繼續執行之前等待一些事情的發生。需要滿足一定條件的進程可以等待一個條件變量，直到其它進程修改了條件變量來告訴它們繼續執行。

Python 中，任何數量的進程都可以使用condition.wait()方法，用信號告知它們正在等待某個條件。在調用該方法之後，它們會自動等待到其它進程調用了condition.notify()或condition.notifyAll()函數。notify()方法值喚醒一個進程，其它進程仍舊等待。notifyAll()方法喚醒所有等待中的進程。每個方法在不同情形中都很實用。

由於條件變量通常和決定條件是否為真的共享變量相聯繫，它們也提供了acquire()和release()方法。這些方法應該在修改可能改變條件狀態的變量時使用。任何想要用信號告知條件已經改變的進程，必須首先使用acquire()來訪問它。

在我們的例子中，在執行第二步之前必須滿足的條件是，兩個進程都必須完成了第一步。我們可以跟蹤已經完成第一步的進程數量，以及條件是否被滿足，通過引入下面兩個變量：

step1_finished = 0
start_step2 = Condition()

我們在do_step_2的開頭插入start_step_2().wait()。每個進程都會在完成步驟 1 之後自增step1_finished，但是我們只會在step_1_finished = 2時發送信號。下面的偽代碼展示了它：

step1_finished = 0
start_step2 = Condition()

def do_step_1(index):
  A[index] = B[index] + C[index]
  # access the shared state that determines the condition status
  start_step2.acquire()
  step1_finished += 1
  if(step1_finished == 2): # if the condition is met
        start_step2.notifyAll() # send the signal
  #release access to shared state
  start_step2.release()

def do_step_2(index):
  # wait for the condition
  start_step2.wait()
  V[index] = M[index] . A

在引入條件變量之後，兩個進程會一起進入步驟 2，像下面這樣：

P1                            P2
read B1: 2
read C1: 0
calculate 2+0: 2
write 2 -> A1                 read B2: 0
acquire start_step2: ok       read C2: 5
write 1 -> step1_finished     calculate 5+0: 5
step1_finished == 2: false    write 5-> A2
release start_step2: ok       acquire start_step2: ok
start_step2: wait             write 2-> step1_finished
wait                          step1_finished == 2: true
wait                          notifyAll start_step_2: ok
start_step2: ok               start_step2:ok
read M1: (1 2)                read M2: (1 2)
read A:(2 5)
calculate (1 2). (2 5): 12    read A:(2 5)
write 12->V1                  calculate (1 2). (2 5): 12
                              write 12->V2

在進入do_step_2的時候，P1需要在start_step_2之前等待，直到P2自增了step1_finished，發現了它等於 2，之後向條件發送信號。

4.3.5 死鎖

雖然同步方法對保護共享狀態十分有效，但它們也帶來了麻煩。因為它們會導致一個進程等待另一個進程，這些進程就有死鎖的風險。死鎖是一種情形，其中兩個或多個進程被卡住，互相等待對方完成。我們已經提到了忘記釋放某個鎖如何導致進程無限卡住。但是即使acquire()和release()調用的數量正確，程序仍然會構成死鎖。

死鎖的來源是循環等待，像下面展示的這樣。沒有進程能夠繼續執行，因為它們正在等待其它進程，而其它進程也在等待它完成。

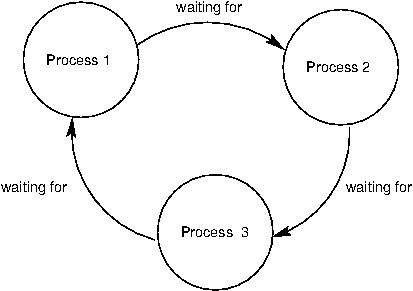
作為一個例子，我們會建立兩個進程的死鎖。假設有兩把鎖，x_lock和y_lock，並且它們像這樣使用：

>>> x_lock = Lock()
>>> y_lock = Lock()
>>> x = 1
>>> y = 0
>>> def compute():
        x_lock.acquire()
        y_lock.acquire()
        y = x + y
        x = x * x
        y_lock.release()
        x_lock.release()
>>> def anti_compute():
        y_lock.acquire()
        x_lock.acquire()
        y = y - x
        x = sqrt(x)
        x_lock.release()
        y_lock.release()

如果compute()和anti_compute()並行執行，並且恰好像下面這樣互相交錯：

P1                          P2
acquire x_lock: ok          acquire y_lock: ok
acquire y_lock: wait        acquire x_lock: wait
wait                        wait
wait                        wait
wait                        wait
...                         ...

所產生的情形就是死鎖。P1和P2每個都持有一把鎖，但是它們需要兩把鎖來執行。P1正在等待P2釋放y_lock，而P2正在等待P1釋放x_lock。所以，沒有進程能夠繼續執行。

4.1 引言

目前為止，我們專注於如何創建、解釋和執行程序。在第一章中，我們學會使用函數作為組合和抽象的手段。第二章展示瞭如何使用數據結構和對象來表示和操作數據，以及向我們介紹了數據抽象的概念。在第三章中，我們學到了計算機程序如何解釋和執行。結果是，我們理解了如何設計程序，它們在單一處理器上運行。

這一章中，我們跳轉到協調多個計算機和處理器的問題。首先，我們會觀察分佈式系統。它們是互相連接的獨立計算機，需要互相溝通來完成任務。它們可能需要協作來提供服務，共享數據，或者甚至是儲存太大而不能在一臺機器上裝下的數據。我們會看到，計算機可以在分佈式系統中起到不同作用，並且瞭解各種信息，計算機需要交換它們來共同工作。

接下來，我們會考慮並行計算。並行計算是這樣，當一個小程序由多個處理器使用共享內存執行時，所有處理器都並行工作來使任務完成得更快。併發（或並行）引入了新的挑戰，並且我們會開發新的機制來管理併發程序的複雜性。

4.2 分佈式系統

分佈式系統是自主的計算機網絡，計算機互相通信來完成一個目標。分佈式系統中的計算機都是獨立的，並且沒有物理上共享的內存或處理器。它們使用消息來和其它計算機通信，消息是網絡上從一臺計算機到另一臺計算機傳輸的一段信息。消息可以用於溝通許多事情：計算機可以讓其它計算機來執行一個帶有特定參數的過程，它們可以發送和接受數據包，或者發送信號讓其它計算機執行特定行為。

分佈式系統中的計算機具有不同的作用。計算機的作用取決於系統的目標，以及計算機自身的硬件和軟件屬性。分佈式系統中，有兩種主要方式來組織計算機，一種叫客戶端-服務端架構（C/S 架構），另一種叫做對等網絡架構（P2P 架構）。

4.2.1 C/S 系統

C/S 架構是一種從中心來源分發服務的方式。只有單個服務端提供服務，多臺客戶端和服務器通信來消耗它的產出。在這個架構中，客戶端和服務端都有不同的任務。服務端的任務就是響應來自客戶端的服務請求，而客戶端的任務就是使用響應中提供的數據來執行一些任務。

C/S 通信模型可以追溯到二十世紀七十年代 Unix 的引入，但這一模型由於現代萬維網（WWW）中的使用而變得具有影響力。一個C/S 交互的例子就是在線閱讀紐約時報。當www.nytimes.com上的服務器與瀏覽器客戶端（比如 Firefox）通信時，它的任務就是發送回來紐約時報主頁的 HTML。這可能涉及到基於發送給服務器的用戶賬戶信息，計算個性化的內容。這意味著需要展示圖片，安排視覺上的內容，展示不同的顏色、字體和圖形，以及允許用戶和渲染後的頁面交互。

客戶端和服務端的概念是強大的函數式抽象。服務端僅僅是一個提供服務的單位，可能同時對應多個客戶端。客戶端是消耗服務的單位。客戶端並不需要知道服務如何提供的細節，或者所獲取的數據如何儲存和計算，服務端也不需要知道數據如何使用。

在網絡上，我們認為客戶端和服務端都是不同的機器，但是，一個機器上的系統也可以擁有 C/S 架構。例如，來自計算機輸入設備的信號需要讓運行在計算機上的程序來訪問。這些程序就是客戶端，消耗鼠標和鍵盤的輸入數據。操作系統的設備驅動就是服務端，接受物理的信號並將它們提供為可用的輸入。

C/S 系統的一個缺陷就是，服務端是故障單點。它是唯一能夠分發服務的組件。客戶端的數量可以是任意的，它們可以交替，並且可以按需出現和消失。但是如果服務器崩潰了，整個系統就會停止工作。所以，由 C/S 架構創建的函數式抽象也使它具有崩潰的風險。

C/S 系統的另一個缺陷是，當客戶端非常多的時候，資源就變得稀缺。客戶端增加系統上的命令而不貢獻任何計算資源。C/S 系統不能隨著不斷變化的需求縮小或擴大。

4.2.2 P2P 系統

C/S 模型適合於服務導向的情形。但是，還有其它計算目標，適合使用更加平等的分工。P2P 的術語用於描述一種分佈式系統，其中勞動力分佈在系統的所有組件中。所有計算機發送並接受數據，它們都貢獻一些處理能力和內存。隨著分佈式系統的規模增長，它的資源計算能力也會增長。在 P2P 系統中，系統的所有組件都對分佈式計算貢獻了一些處理能力和內存。

所有參與者的勞動力的分工是 P2P 系統的識別特徵。也就是說，對等者需要能夠和其它人可靠地通信。為了確保消息到達預定的目的地，P2P 系統需要具有組織良好的網絡結構。這些系統中的組件協作來維護足夠的其它組件的位置信息並將消息發送到預定的目的地。

在一些 P2P 系統中，維護網絡健康的任務由一系列特殊的組件執行。這種系統並不是純粹的 P2P 系統，因為它們具有不同類型的組件類型，提供不同的功能。支持 P2P 網絡的組件就像腳手架那樣：它們有助於網絡保持連接，它們維護不同計算機的位置信息，並且它們新來者來鄰居中找到位置。

P2P 系統的最常見應用就是數據傳送和存儲。對於數據傳送，系統中的每臺計算機都致力於網絡上的數據傳送。如果目標計算機是特定計算機的鄰居，那臺計算機就一起幫助傳送數據。對於數據存儲，數據集可以過於龐大，不能在任何單臺計算機內裝下，或者儲存在單臺計算機內具有風險。每臺計算機都儲存數據的一小部分，不同的計算機上可能會儲存相同數據的多個副本。當一臺計算機崩潰時，上面的數據可以由其它副本恢復，或者在更換替代品之後放回。

Skype，一個音頻和視頻聊天服務，是採用 P2P 架構的數據傳送應用的示例。當不同計算機上的兩個人都使用 Skype 交談時，它們的通信會拆成由 1 和 0 構成的數據包，並且通過 P2P 網絡傳播。這個網絡由電腦上註冊了 Skype 的其它人組成。每臺計算機都知道附近其它人的位置。一臺計算機通過將數據包傳給它的鄰居，來幫助將它傳到目的地，它的鄰居又將它傳給其它鄰居，以此類推，直到數據包到達了它預定的目的地。Skype 並不是純粹的 P2P 系統。一個超級節點組成的腳手架網絡用於用戶登錄和退出，維護它們的計算機的位置信息，並且修改網絡結構來處理用戶進入和離開。

4.2.3 模塊化

我們剛才考慮的兩個架構 -- P2P 和 C/S -- 都為強制模塊化而設計。模塊化是一個概念，系統的組件對其它組件來說應該是個黑盒。組件如何實現行為應該並不重要，只要它提供了一個接口：規定了輸入應該產生什麼輸出。

在第二章中，我們在調度函數和麵向對象編程的上下文中遇到了接口。這裡，接口的形式為指定對象應接收的信息，以及對象應如何響應它們。例如，為了提供“表示為字符串”的接口，對象必須回覆__repr__和__str__信息，並且在響應中輸出合適的字符串。那些字符串的生成如何實現並不是接口的一部分。

在分佈式系統中，我們必須考慮涉及到多臺計算機的程序設計，所以我們將接口的概念從對象和消息擴展為整個程序。接口指定了應該接受的輸入，以及應該在響應中返回給輸入的輸出。

接口在真實世界的任何地方都存在，我們經常習以為常。一個熟悉的例子就是 TV 遙控器。你可以買到許多牌子的遙控器或者 TV，它們都能工作。它們的唯一共同點就是“TV 遙控器”的接口。只要當你按下電院、音量、頻道或者其它任何按鈕（輸入）時，一塊電路向你的 TV 發送正確的信號（輸出），它就遵循“TV 遙控器”接口。

模塊化給予系統許多好處，並且是一種沉思熟慮的系統設計。首先，模塊化的系統易於理解。這使它易於修改和擴展。其次，如果系統中什麼地方發生錯誤，只需要更換有錯誤的組件。再者，bug 或故障可以輕易定位。如果組件的輸出不符合接口的規定，而且輸入是正確的，那麼這個組件就是故障來源。

4.2.4 消息傳遞

在分佈式系統中，組件使用消息傳遞來互相溝通。消息有三個必要部分：發送者、接收者和內容。發送者需要被指定，便於接受者得知哪個組件發送了信息，以及將回復發送到哪裡。接收者需要被指定，便於任何協助發送消息的計算機知道發送到哪裡。消息的內容是最寶貴的。取決於整個系統的函數，內容可以是一段數據、一個信號，或者一條指令，讓遠程計算機來以一些參數求出某個函數。

消息傳遞的概念和第二章的消息傳遞機制有很大關係，其中，調度函數或字典會響應值為字符串的信息。在程序中，發送者和接受者都由求值規則標識。但是在分佈式系統中，接受者和發送者都必須顯式編碼進消息中。在程序中，使用字符串來控制調度函數的行為十分方便。在分佈式系統中，消息需要經過網絡發送，並且可能需要存放許多不同種類的信號作為“數據”，所以它們並不始終編碼為字符串。但是在兩種情況中，消息都服務於相同的函數。不同的組件（調度函數或計算機）交換消息來完成一個目標，它需要多個組件模塊的協作。

在較高層面上，消息內容可以是複雜的數據結構，但是在較低層面上，消息只是簡單的 1 和 0 的流，在網絡上傳輸。為了變得易用，所有網絡上發送的消息都需要根據一致的消息協議格式化。

消息協議是一系列規則，用於編碼和解碼消息。許多消息協議規定，消息必須符合特定的格式，其中特定的比特具有固定的含義。固定的格式實現了固定的編碼和解碼規則來生成和讀取這種格式。分佈式系統中的所有組件都必須理解協議來互相通信。這樣，它們就知道消息的哪個部分對應哪個信息。

消息協議並不是特定的程序或軟件庫。反之，它們是可以由大量程序使用的規則，甚至以不同的編程語言編寫。所以，帶有大量不同軟件系統的計算機可以加入相同的分佈式系統，只需要遵守控制這個系統的消息協議。

4.2.5 萬維網上的消息

HTTP（超文本傳輸協議的縮寫）是萬維網所支持的消息協議。它指定了在 Web 瀏覽器和服務器之間交換的消息格式。所有 Web 瀏覽器都使用 HTTP 協議來請求服務器上的頁面，而且所有 Web 服務器都使用 HTTP 格式來發回它們的響應。

當你在 Web 瀏覽器上鍵入 URL 時，比如 http://en.wikipedia.org/wiki/UC_Berkeley，你實際上就告訴了你的計算機，使用 "HTTP" 協議，從 "http://en.wikipedia.org/wiki/UC_Berkeley" 的服務器上請求 "wiki/UC_Berkeley" 頁面。消息的發送者是你的計算機，接受者是 en.wikipedia.org，以及消息內容的格式是：

GET /wiki/UC_Berkeley HTTP/1.1

第一個單詞是請求類型，下一個單詞是所請求的資源，之後是協議名稱（HTTP）和版本（1.1）。（請求還有其它類型，例如 PUT、POST 和 HEAD，Web 瀏覽器也會使用它們。）

服務器發回了回覆。這時，發送者是 en.wikipedia.org，接受者是你的計算機，消息內容的格式是由數據跟隨的協議頭：

HTTP/1.1 200 OK
Date: Mon, 23 May 2011 22:38:34 GMT
Server: Apache/1.3.3.7 (Unix) (Red-Hat/Linux)
Last-Modified: Wed, 08 Jan 2011 23:11:55 GMT
Content-Type: text/html; charset=UTF-8

... web page content ...

第一行，單詞 "200 OK" 表示沒有發生錯誤。協議頭下面的行提供了有關服務器的信息，日期和發回的內容類型。協議頭和頁面的實際內容通過一個空行來分隔。

如果你鍵入了錯誤的 Web 地址，或者點擊了死鏈，你可能會看到類似於這個錯誤的消息：

404 Error File Not Found

它的意思是服務器發送回了一個 HTTP 協議頭，以這樣起始：

HTTP/1.1 404 Not Found

一系列固定的響應代碼是消息協議的普遍特性。協議的設計者試圖預料通過協議發送的常用消息，並且賦為固定的代碼來減少傳送大小，以及建立通用的消息語義。在 HTTP 協議中，200 響應代碼表示成功，而 404 表示資源沒有找到的錯誤。其它大量響應代碼也存在於 HTTP 1.1 標準中。

HTTP 是用於通信的固定格式，但是它允許傳輸任意的 Web 頁面。其它互聯網上的類似協議是 XMPP，即時消息的常用協議，以及 FTP，用於在客戶端和服務器之間下載和上傳文件的協議。

4.3 並行計算

計算機每一年都會變得越來越快。在 1965 年，英特爾聯合創始人戈登·摩爾預測了計算機將如何隨時間而變得越來越快。僅僅基於五個數據點，他推測，一個芯片中的晶體管數量每兩年將翻一倍。近50年後，他的預測仍驚人地準確，現在稱為摩爾定律。

儘管速度在爆炸式增長，計算機還是無法跟上可用數據的規模。根據一些估計，基因測序技術的進步將使可用的基因序列數據比處理器變得更快的速度還要快。換句話說，對於遺傳數據，計算機變得越來越不能處理每年需要處理的問題規模，即使計算機本身變得越來越快。

為了規避對單個處理器速度的物理和機械約束，製造商正在轉向另一種解決方案：多處理器。如果兩個，或三個，或更多的處理器是可用的，那麼許多程序可以更快地執行。當一個處理器在做一些計算的一個切面時，其他的可以在另一個切面工作。所有處理器都可以共享相同的數據，但工作並行執行。

為了能夠合作，多個處理器需要能夠彼此共享信息。這通過使用共享內存環境來完成。該環境中的變量、對象和數據結構對所有的進程可見。處理器在計算中的作用是執行編程語言的求值和執行規則。在一個共享內存模型中，不同的進程可能執行不同的語句，但任何語句都會影響共享環境。

4.3.1 共享狀態的問題

多個進程之間的共享狀態具有單一進程環境沒有的問題。要理解其原因，讓我們看看下面的簡單計算：

x = 5
x = square(x)
x = x + 1

x的值是隨時間變化的。起初它是 5，一段時間後它是 25，最後它是 26。在單一處理器的環境中，沒有時間依賴性的問題。x的值在結束時總是 26。但是如果存在多個進程，就不能這樣說了。假設我們並行執行了上面代碼的最後兩行：一個處理器執行x = square(x)而另一個執行x = x + 1。每一個這些賦值語句都包含查找當前綁定到x的值，然後使用新值更新綁定。讓我們假設x是共享的，同一時間只有一個進程讀取或寫入。即使如此，讀和寫的順序可能會有所不同。例如，下面的例子顯示了兩個進程的每個進程的一系列步驟，P1和P2。每一步都是簡要描述的求值過程的一部分，隨時間從上到下執行：

P1                    P2
read x: 5
                      read x: 5
calculate 5*5: 25     calculate 5+1: 6
write 25 -> x
                      write x-> 6

在這個順序中，x的最終值為 6。如果我們不協調這兩個過程，我們可以得到另一個順序的不同結果：

P1                    P2
                      read x: 5
read x: 5             calculate 5+1: 6
calculate 5*5: 25     write x->6
write 25 -> x

在這個順序中，x將是 25。事實上存在多種可能性，這取決於進程執行代碼行的順序。x的最終值可能最終為 5，25，或預期值 26。

前面的例子是無價值的。square(x)和x = x + 1是簡單快速的計算。我們強迫一條語句跑在另一條的後面，並不會失去太多的時間。但是什麼樣的情況下，並行化是必不可少的？這種情況的一個例子是銀行業。在任何給定的時間，可能有成千上萬的人想用他們的銀行賬戶進行交易：他們可能想在商店刷卡，存入支票，轉帳，或支付賬單。即使一個帳戶在同一時間也可能有活躍的多個交易。

讓我們看看第二章的make_withdraw函數，下面是修改過的版本，在更新餘額之後打印而不是返回它。我們感興趣的是這個函數將如何併發執行。

>>> def make_withdraw(balance):
        def withdraw(amount):
            nonlocal balance
            if amount > balance:
                print('Insufficient funds')
            else:
                balance = balance - amount
                print(balance)
        return withdraw

現在想象一下，我們以 10 美元創建一個帳戶，讓我們想想，如果我們從帳戶中提取太多的錢會發生什麼。如果我們順序執行這些交易，我們會收到資金不足的消息。

>>> w = make_withdraw(10)
>>> w(8)
2
>>> w(7)
'Insufficient funds'

但是，在並行中可以有許多不同的結果。下面展示了一種可能性：

P1: w(8)                        P2: w(7)
read balance: 10
read amount: 8                  read balance: 10
8 > 10: False                   read amount: 7
if False                        7 > 10: False
10 - 8: 2                       if False
write balance -> 2              10 - 7: 3
read balance: 2                 write balance -> 3
print 2                         read balance: 3
                                print 3

這個特殊的例子給出了一個不正確結果 3。就好像w(8)交易從來沒有發生過。其他可能的結果是 2，和'Insufficient funds'。這個問題的根源是：如果P2 在P1寫入值前讀取餘額，P2的狀態是不一致的（反之亦然）。P2所讀取的餘額值是過時的，因為P1打算改變它。P2不知道，並且會用不一致的值覆蓋它。

這個例子表明，並行化的代碼不像把代碼行分給多個處理器來執行那樣容易。變量讀寫的順序相當重要。

一個保證執行正確性的有吸引力的方式是，兩個修改共享數據的程序不能同時執行。不幸的是，對於銀行業這將意味著，一次只可以進行一個交易，因為所有的交易都修改共享數據。直觀地說，我們明白，讓 2 個不同的人同時進行完全獨立的帳戶交易應該沒有問題。不知何故，這兩個操作不互相干擾，但在同一帳戶上的相同方式的同時操作就相互干擾。此外，當進程不讀取或寫入時，讓它們同時運行就沒有問題。

4.3.2 並行計算的正確性

並行計算環境中的正確性有兩個標準。第一個是，結果應該總是相同。第二個是，結果應該和串行執行的結果一致。

第一個條件表明，我們必須避免在前面的章節中所示的變化，其中在不同的方式下的交叉讀寫會產生不同的結果。例子中，我們從 10 美元的帳戶取出了w(8)和w(7)。這個條件表明，我們必須始終返回相同的答案，獨立於P1和P2的指令執行順序。無論如何，我們必須以這樣一種方式來編寫我們的程序，無論他們如何相互交叉，他們應該總是產生同樣的結果。

第二個條件揭示了許多可能的結果中哪個是正確的。例子中，我們從 10 美元的帳戶取出了w(8)和w(7)，這個條件表明結果必須總是餘額不足，而不是 2 或者 3。

當一個進程在程序的臨界區影響另一個進程時，並行計算中就會出現問題。這些都是需要執行的代碼部分，它們看似是單一的指令，但實際上由較小的語句組成。一個程序會以一系列原子硬件指令執行，由於處理器的設計，這些是不能被打斷或分割為更小單元的指令。為了在並行的情況下表現正確，程序代碼的臨界區需要具有原子性，保證他們不會被任何其他代碼中斷。

為了強制程序臨界區在併發下的原子性，需要能夠在重要的時刻將進程序列化或彼此同步。序列化意味著同一時間只運行一個進程 -- 這一瞬間就好像串行執行一樣。同步有兩種形式。首先是互斥，進程輪流訪問一個變量。其次是條件同步，在滿足條件（例如其他進程完成了它們的任務）之前進程一直等待，之後繼續執行。這樣，當一個程序即將進入臨界區時，其他進程可以一直等待到它完成，然後安全地執行。

4.3.3 保護共享狀態：鎖和信號量

在本節中討論的所有同步和序列化方法都使用相同的基本思想。它們在共享狀態中將變量用作信號，所有過程都會理解並遵守它。這是一個相同的理念，允許分佈式系統中的計算機協同工作 -- 它們通過傳遞消息相互協調，根據每一個參與者都理解和遵守的一個協議。

這些機制不是為了保護共享狀態而出現的物理障礙。相反，他們是建立相互理解的基礎上。和出現在十字路口的各種方向的車輛能夠安全通行一樣，是同一種相互理解。這裡沒有物理的牆壁阻止汽車相撞，只有遵守規則，紅色意味著“停止”，綠色意味著“通行”。同樣，沒有什麼可以保護這些共享變量，除非當一個特定的信號表明輪到某個進程了，進程才會訪問它們。

**鎖。**鎖，也被稱為互斥體（mutex），是共享對象，常用於發射共享狀態被讀取或修改的信號。不同的編程語言實現鎖的方式不同，但是在 Python 中，一個進程可以調用acquire()方法來嘗試獲得鎖的“所有權”，然後在使用完共享變量的時候調用release()釋放它。當進程獲得了一把鎖，任何試圖執行acquire()操作的其他進程都會自動等待到鎖被釋放。這樣，同一時間只有一個進程可以獲得一把鎖。

對於一把保護一組特定的變量的鎖，所有的進程都需要編程來遵循一個規則：一個進程不擁有特定的鎖就不能訪問相應的變量。實際上，所有進程都需要在鎖的acquire()和release()語句之間“包裝”自己對共享變量的操作。

我們可以把這個概念用於銀行餘額的例子中。該示例的臨界區是從餘額讀取到寫入的一組操作。我們看到，如果一個以上的進程同時執行這個區域，問題就會發生。為了保護臨界區，我們需要使用一把鎖。我們把這把鎖稱為balance_lock（雖然我們可以命名為任何我們喜歡的名字）。為了鎖定實際保護的部分，我們必須確保試圖進入這部分時調用acquire()獲取鎖，以及之後調用release()釋放鎖，這樣可以輪到別人。

>>> from threading import Lock
>>> def make_withdraw(balance):
        balance_lock = Lock()
        def withdraw(amount):
            nonlocal balance
            # try to acquire the lock
            balance_lock.acquire()
            # once successful, enter the critical section
            if amount > balance:
                print("Insufficient funds")
            else:
                balance = balance - amount
                print(balance)
            # upon exiting the critical section, release the lock
            balance_lock.release()

如果我們建立和之前一樣的情形：

w = make_withdraw(10)

現在就可以並行執行w(8)和w(7)了：

P1                                  P2
acquire balance_lock: ok
read balance: 10                    acquire balance_lock: wait
read amount: 8                      wait
8 > 10: False                       wait
if False                            wait
10 - 8: 2                           wait
write balance -> 2                  wait
read balance: 2                     wait
print 2                             wait
release balance_lock                wait
                                    acquire balance_lock:ok
                                    read balance: 2
                                    read amount: 7
                                    7 > 2: True
                                    if True
                                    print 'Insufficient funds'
                                    release balance_lock

我們看到了，兩個進程同時進入臨界區是可能的。某個進程實例獲取到了balance_lock，另一個就得等待，直到那個進程退出了臨界區，它才能開始執行。

要注意程序不會自己終止，除非P1釋放了balance_lock。如果它沒有釋放balance_lock，P2永遠不可能獲取它，而是一直會等待。忘記釋放獲得的鎖是並行編程中的一個常見錯誤。

**信號量。**信號量是用於維持有限資源訪問的信號。它們和鎖類似，除了它們可以允許某個限制下的多個訪問。它就像電梯一樣只能夠容納幾個人。一旦達到了限制，想要使用資源的進程就必須等待。其它進程釋放了信號量之後，它才可以獲得。

例如，假設有許多進程需要讀取中心數據庫服務器的數據。如果過多的進程同時訪問它，它就會崩潰，所以限制連接數量就是個好主意。如果數據庫只能同時支持N=2的連接，我們就可以以初始值N=2來創建信號量。

>>> from threading import Semaphore
>>> db_semaphore = Semaphore(2) # set up the semaphore
>>> database = []
>>> def insert(data):
        db_semaphore.acquire() # try to acquire the semaphore
        database.append(data)  # if successful, proceed
        db_semaphore.release() # release the semaphore
>>> insert(7)
>>> insert(8)
>>> insert(9)

信號量的工作機制是，所有進程只在獲取了信號量之後才可以訪問數據庫。只有N=2個進程可以獲取信號量，其它的進程都需要等到其中一個進程釋放了信號量，之後在訪問數據庫之前嘗試獲取它。

P1                          P2                           P3
acquire db_semaphore: ok    acquire db_semaphore: wait   acquire db_semaphore: ok
read data: 7                wait                         read data: 9
append 7 to database        wait                         append 9 to database
release db_semaphore: ok    acquire db_semaphore: ok     release db_semaphore: ok
                            read data: 8
                            append 8 to database
                            release db_semaphore: ok

值為 1 的信號量的行為和鎖一樣。

4.3.4 保持同步：條件變量

條件變量在並行計算由一系列步驟組成時非常有用。進程可以使用條件變量，來用信號告知它完成了特定的步驟。之後，等待信號的其它進程就會開始它們的任務。一個需要逐步計算的例子就是大規模向量序列的計算。在計算生物學，Web 範圍的計算，和圖像處理及圖形學中，常常需要處理非常大型（百萬級元素）的向量和矩陣。想象下面的計算：

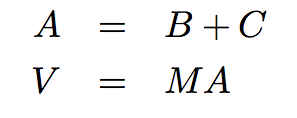
我們可以通過將矩陣和向量按行拆分，並把每一行分配到單獨的線程上，來並行處理每一步。作為上面的計算的一個實例，想象下面的簡單值：

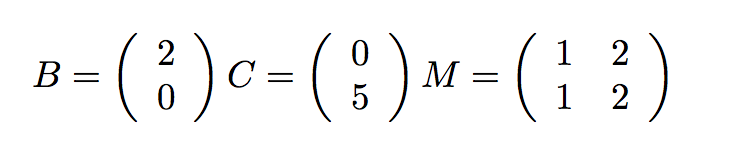
我們將前一半（這裡是第一行）分配給一個線程，後一半（第二行）分配給另一個線程：

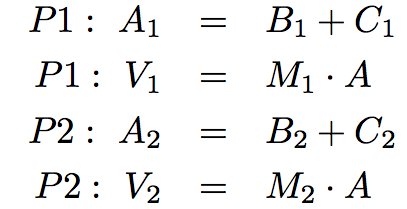
在偽代碼中，計算是這樣的：

def do_step_1(index):
  A[index] = B[index] + C[index]

def do_step_2(index):
        V[index] = M[index] . A

進程 1 執行了：

do_step_1(1)
do_step_2(1)

進程 2 執行了：

do_step_1(2)
do_step_2(2)

如果允許不帶同步處理，就造成下面的不一致性：

P1                          P2
read B1: 2
read C1: 0
calculate 2+0: 2
write 2 -> A1               read B2: 0
read M1: (1 2)              read C2: 5
read A: (2 0)               calculate 5+0: 5
calculate (1 2).(2 0): 2    write 5 -> A2
write 2 -> V1               read M2: (1 2)
                            read A: (2 5)
                            calculate (1 2).(2 5):12
                            write 12 -> V2

問題就是V直到所有元素計算出來時才會計算出來。但是，P1在A的所有元素計算出來之前，完成A = B+C並且移到V = MA。所以它與M相乘時使用了A的不一致的值。

我們可以使用條件變量來解決這個問題。

條件變量是表現為信號的對象，信號表示某個條件被滿足。它們通常被用於協調進程，這些進程需要在繼續執行之前等待一些事情的發生。需要滿足一定條件的進程可以等待一個條件變量，直到其它進程修改了條件變量來告訴它們繼續執行。

Python 中，任何數量的進程都可以使用condition.wait()方法，用信號告知它們正在等待某個條件。在調用該方法之後，它們會自動等待到其它進程調用了condition.notify()或condition.notifyAll()函數。notify()方法值喚醒一個進程，其它進程仍舊等待。notifyAll()方法喚醒所有等待中的進程。每個方法在不同情形中都很實用。

由於條件變量通常和決定條件是否為真的共享變量相聯繫，它們也提供了acquire()和release()方法。這些方法應該在修改可能改變條件狀態的變量時使用。任何想要用信號告知條件已經改變的進程，必須首先使用acquire()來訪問它。

在我們的例子中，在執行第二步之前必須滿足的條件是，兩個進程都必須完成了第一步。我們可以跟蹤已經完成第一步的進程數量，以及條件是否被滿足，通過引入下面兩個變量：

step1_finished = 0
start_step2 = Condition()

我們在do_step_2的開頭插入start_step_2().wait()。每個進程都會在完成步驟 1 之後自增step1_finished，但是我們只會在step_1_finished = 2時發送信號。下面的偽代碼展示了它：

step1_finished = 0
start_step2 = Condition()

def do_step_1(index):
  A[index] = B[index] + C[index]
  # access the shared state that determines the condition status
  start_step2.acquire()
  step1_finished += 1
  if(step1_finished == 2): # if the condition is met
        start_step2.notifyAll() # send the signal
  #release access to shared state
  start_step2.release()

def do_step_2(index):
  # wait for the condition
  start_step2.wait()
  V[index] = M[index] . A

在引入條件變量之後，兩個進程會一起進入步驟 2，像下面這樣：

P1                            P2
read B1: 2
read C1: 0
calculate 2+0: 2
write 2 -> A1                 read B2: 0
acquire start_step2: ok       read C2: 5
write 1 -> step1_finished     calculate 5+0: 5
step1_finished == 2: false    write 5-> A2
release start_step2: ok       acquire start_step2: ok
start_step2: wait             write 2-> step1_finished
wait                          step1_finished == 2: true
wait                          notifyAll start_step_2: ok
start_step2: ok               start_step2:ok
read M1: (1 2)                read M2: (1 2)
read A:(2 5)
calculate (1 2). (2 5): 12    read A:(2 5)
write 12->V1                  calculate (1 2). (2 5): 12
                              write 12->V2

在進入do_step_2的時候，P1需要在start_step_2之前等待，直到P2自增了step1_finished，發現了它等於 2，之後向條件發送信號。

4.3.5 死鎖

雖然同步方法對保護共享狀態十分有效，但它們也帶來了麻煩。因為它們會導致一個進程等待另一個進程，這些進程就有死鎖的風險。死鎖是一種情形，其中兩個或多個進程被卡住，互相等待對方完成。我們已經提到了忘記釋放某個鎖如何導致進程無限卡住。但是即使acquire()和release()調用的數量正確，程序仍然會構成死鎖。

死鎖的來源是循環等待，像下面展示的這樣。沒有進程能夠繼續執行，因為它們正在等待其它進程，而其它進程也在等待它完成。

作為一個例子，我們會建立兩個進程的死鎖。假設有兩把鎖，x_lock和y_lock，並且它們像這樣使用：

>>> x_lock = Lock()
>>> y_lock = Lock()
>>> x = 1
>>> y = 0
>>> def compute():
        x_lock.acquire()
        y_lock.acquire()
        y = x + y
        x = x * x
        y_lock.release()
        x_lock.release()
>>> def anti_compute():
        y_lock.acquire()
        x_lock.acquire()
        y = y - x
        x = sqrt(x)
        x_lock.release()
        y_lock.release()

如果compute()和anti_compute()並行執行，並且恰好像下面這樣互相交錯：

P1                          P2
acquire x_lock: ok          acquire y_lock: ok
acquire y_lock: wait        acquire x_lock: wait
wait                        wait
wait                        wait
wait                        wait
...                         ...

所產生的情形就是死鎖。P1和P2每個都持有一把鎖，但是它們需要兩把鎖來執行。P1正在等待P2釋放y_lock，而P2正在等待P1釋放x_lock。所以，沒有進程能夠繼續執行。

第五章 序列和協程

來源：Chapter 5: Sequences and Coroutines

譯者：飛龍

協議：CC BY-NC-SA 4.0

5.1 引言

在這一章中，我們通過開發新的工具來處理有序數據，繼續討論真實世界中的應用。在第二章中，我們介紹了序列接口，在 Python 內置的數據類型例如tuple和list中實現。序列支持兩個操作：獲取長度和由下標訪問元素。第三章中，我們開發了序列接口的用戶定義實現，用於表示遞歸列表的Rlist類。序列類型具有高效的表現力，並且可以讓我們高效訪問大量有序數據集。

但是，使用序列抽象表示有序數據有兩個重要限制。第一個是長度為n的序列的要佔據比例為n的內存總數。於是，序列越長，表示它所佔的內存空間就越大。

第二個限制是，序列只能表示已知且長度有限的數據集。許多我們想要表示的有序集合並沒有定義好的長度，甚至有些是無限的。兩個無限序列的數學示例是正整數和斐波那契數。無限長度的有序數據集也出現在其它計算領域，例如，所有推特狀態的序列每秒都在增長，所以並沒有固定的長度。與之類似，經過基站發送出的電話呼叫序列，由計算機用戶發出的鼠標動作序列，以及飛機上的傳感器產生的加速度測量值序列，都在世界演化過程中無限擴展。

在這一章中，我們介紹了新的構造方式用於處理有序數據，它為容納未知或無限長度的集合而設計，但僅僅使用有限的內存。我們也會討論這些工具如何用於一種叫做協程的程序結構，來創建高效、模塊化的數據處理流水線。

5.2 隱式序列

序列可以使用一種程序結構來表示，它不將每個元素顯式儲存在內存中，這是高效處理有序數據的核心概念。為了將這個概念用於實踐，我們需要構造對象來提供序列中所有元素的訪問，但是不要事先把所有元素計算出來並儲存。

這個概念的一個簡單示例就是第二章出現的range序列類型。range表示連續有界的整數序列。但是，它的每個元素並不顯式在內存中表示，當元素從range中獲取時，才被計算出來。所以，我們可以表示非常大的整數範圍。只有範圍的結束位置才被儲存為range對象的一部分，元素都被憑空計算出來。

>>> r = range(10000, 1000000000)
>>> r[45006230]
45016230

這個例子中，當構造範圍示例時，並不是這個範圍內的所有 999,990,000 個整數都被儲存。反之，範圍對象將第一個元素 10,000 與下標相加 45,006,230 來產生第 45,016,230 個元素。計算所求的元素值並不從現有的表示中獲取，這是惰性計算的一個例子。計算機科學將惰性作為一種重要的計算工具加以讚揚。

迭代器是提供底層有序數據集的有序訪問的對象。迭代器在許多編程語言中都是內建對象，包括 Python。迭代器抽象擁有兩個組成部分：一種獲取底層元素序列的下一個元素的機制，以及一種標識元素序列已經到達末尾，沒有更多剩餘元素的機制。在帶有內建對象系統的編程語言中，這個抽象通常相當於可以由類實現的特定接口。Python 的迭代器接口會在下一節中描述。

迭代器的實用性來源於一個事實，底層數據序列並不能顯式在內存中表達。迭代器提供了一種機制，可以依次計算序列中的每個值，但是所有元素不需要連續儲存。反之，當下個元素從迭代器獲取的時候，這個元素會按照請求計算，而不是從現有的內存來源中獲取。

範圍可以惰性計算序列中的元素，因為序列的表示是統一的，並且任何元素都可以輕易從範圍的起始和結束位置計算出來。迭代器支持更廣泛的底層有序數據集的惰性生成，因為它們不需要提供底層序列任意元素的訪問途徑。反之，它們僅僅需要按照順序，在每次其它元素被請求的時候，計算出序列的下一個元素。雖然不像序列可訪問任意元素那樣靈活（叫做隨機訪問），有序數據序列的順序訪問對於數據處理應用來說已經足夠了。

5.2.1 Python 迭代器

Python 迭代器接口包含兩個消息。__next__消息向迭代器獲取所表示的底層序列的下一個元素。為了對__next__方法調用做出回應，迭代器可以執行任何計算來獲取或計算底層數據序列的下一個元素。__next__的調用讓迭代器產生變化：它們向前移動迭代器的位置。所以多次調用__next__會有序返回底層序列的元素。在__next__的調用過程中，Python 通過StopIteration異常，來表示底層數據序列已經到達末尾。

下面的Letters類迭代了從a到d字母的底層序列。成員變量current儲存了序列中的當前字母。__next__方法返回這個字母，並且使用它來計算current的新值。

>>> class Letters(object):
        def __init__(self):
            self.current = 'a'
        def __next__(self):
            if self.current > 'd':
                raise StopIteration
            result = self.current
            self.current = chr(ord(result)+1)
            return result
        def __iter__(self):
            return self

__iter__消息是 Python 迭代器所需的第二個消息。它只是簡單返回迭代器，它對於提供迭代器和序列的通用接口很有用，在下一節會描述。

使用這個類，我們就可以訪問序列中的字母：

>>> letters = Letters()
>>> letters.__next__()
'a'
>>> letters.__next__()
'b'
>>> letters.__next__()
'c'
>>> letters.__next__()
'd'
>>> letters.__next__()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 12, in next
StopIteration

Letters示例只能迭代一次。一旦__next__()方法產生了StopIteration異常，它就從此之後一直這樣了。除非創建新的實例，否則沒有辦法來重置它。

迭代器也允許我們表示無限序列，通過實現永遠不會產生StopIteration異常的__next__方法。例如，下面展示的Positives類迭代了正整數的無限序列：

>>> class Positives(object):
        def __init__(self):
            self.current = 0;
        def __next__(self):
            result = self.current
            self.current += 1
            return result
        def __iter__(self):
            return self

5.2.2 for語句

Python 中，序列可以通過實現__iter__消息用於迭代。如果一個對象表示有序數據，它可以在for語句中用作可迭代對象，通過回應__iter__消息來返回迭代器。這個迭代器應擁有__next__()方法，依次返回序列中的每個元素，最後到達序列末尾時產生StopIteration異常。

>>> counts = [1, 2, 3]
>>> for item in counts:
        print(item)
1
2
3

在上面的實例中，counts列表返回了迭代器，作為__iter__()方法調用的回應。for語句之後反覆調用迭代器的__next__()方法，並且每次都將返回值賦給item。這個過程一直持續，直到迭代器產生了StopIteration異常，這時for語句就終止了。

使用我們關於迭代器的知識，我們可以拿while、賦值和try語句實現for語句的求值規則：

>>> i = counts.__iter__()
>>> try:
        while True:
            item = i.__next__()
            print(item)
    except StopIteration:
        pass
1
2
3

在上面，調用counts的__iter__方法所返回的迭代器綁定到了名稱i上面，便於依次獲取每個元素。StopIteration異常的處理子句不做任何事情，但是這個異常的處理提供了退出while循環的控制機制。

5.2.3 生成器和yield語句

上面的Letters和Positives對象需要我們引入一種新的字段，self.current，來跟蹤序列的處理過程。在上面所示的簡單序列中，這可以輕易實現。但對於複雜序列，__next__()很難在計算中節省空間。生成器允許我們通過利用 Python 解釋器的特性定義更復雜的迭代。

生成器是由一類特殊函數，叫做生成器函數返回的迭代器。生成器函數不同於普通的函數，因為它不在函數體中包含return語句，而是使用yield語句來返回序列中的元素。

生成器不使用任何對象屬性來跟蹤序列的處理過程。它們控制生成器函數的執行，每次__next__方法調用時，它們執行到下一個yield語句。Letters迭代可以使用生成器函數實現得更加簡潔。

>>> def letters_generator():
        current = 'a'
        while current <= 'd':
            yield current
            current = chr(ord(current)+1)
>>> for letter in letters_generator():
        print(letter)
a
b
c
d

即使我們永不顯式定義__iter__()或__next__()方法，Python 會理解當我們使用yield語句時，我們打算定義生成器函數。調用時，生成器函數並不返回特定的產出值，而是返回一個生成器（一種迭代器），它自己就可以返回產出的值。生成器對象擁有__iter__和__next__方法，每個對__next__的調用都會從上次停留的地方繼續執行生成器函數，直到另一個yield語句執行的地方。

__next__第一次調用時，程序從letters_generator的函數體一直執行到進入yield語句。之後，它暫停並返回current值。yield語句並不破壞新創建的環境，而是為之後的使用保留了它。當__next__再次調用時，執行在它停留的地方恢復。letters_generator作用域中current和任何所綁定名稱的值都會在隨後的__next__調用中保留。

我們可以通過手動調用__next__()來遍歷生成器：

>>> letters = letters_generator()
>>> type(letters)
<class 'generator'>
>>> letters.__next__()
'a'
>>> letters.__next__()
'b'
>>> letters.__next__()
'c'
>>> letters.__next__()
'd'
>>> letters.__next__()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
StopIteration

在第一次__next__()調用之前，生成器並不會開始執行任何生成器函數體中的語句。

5.2.4 可迭代對象

Python 中，迭代只會遍歷一次底層序列的元素。在遍歷之後，迭代器在__next__()調用時會產生StopIteration異常。許多應用需要迭代多次元素。例如，我們需要對一個列表迭代多次來枚舉所有的元素偶對：

>>> def all_pairs(s):
        for item1 in s:
            for item2 in s:
                yield (item1, item2)
>>> list(all_pairs([1, 2, 3]))
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]

序列本身不是迭代器，但是它是可迭代對象。Python 的可迭代接口只包含一個消息，__iter__，返回一個迭代器。Python 中內建的序列類型在__iter__方法調用時，返回迭代器的新實例。如果一個可迭代對象在每次調用__iter__時返回了迭代器的新實例，那麼它就能被迭代多次。

新的可迭代類可以通過實現可迭代接口來定義。例如，下面的可迭代對象LetterIterable類在每次調用__iter__時返回新的迭代器來迭代字母。

>>> class LetterIterable(object):
        def __iter__(self):
            current = 'a'
            while current <= 'd':
                yield current
                current = chr(ord(current)+1)

__iter__方法是個生成器函數，它返回一個生成器對象，產出從'a'到'd'的字母。

Letters迭代器對象在單次迭代之後就被“用完”了，但是LetterIterable對象可被迭代多次。所以，LetterIterable示例可以用於all_pairs的參數。

>>> letters = LetterIterable()
>>> all_pairs(letters).__next__()
('a', 'a')

5.2.5 流

流提供了一種隱式表示有序數據的最終方式。流是惰性計算的遞歸列表。就像第三章的Rlist類那樣，Stream實例可以響應對其第一個元素和剩餘部分的獲取請求。同樣，Stream的剩餘部分還是Stream。然而不像RList，流的剩餘部分只在查找時被計算，而不是事先存儲。也就是說流的剩餘部分是惰性計算的。

為了完成這個惰性求值，流會儲存計算剩餘部分的函數。無論這個函數在什麼時候調用，它的返回值都作為流的一部分，儲存在叫做_rest的屬性中。下劃線表示它不應直接訪問。可訪問的屬性rest是個方法，它返回流的剩餘部分，並在必要時計算它。使用這個設計，流可以儲存計算剩餘部分的方式，而不用總是顯式儲存它們。

>>> class Stream(object):
        """A lazily computed recursive list."""
        def __init__(self, first, compute_rest, empty=False):
            self.first = first
            self._compute_rest = compute_rest
            self.empty = empty
            self._rest = None
            self._computed = False
        @property
        def rest(self):
            """Return the rest of the stream, computing it if necessary."""
            assert not self.empty, 'Empty streams have no rest.'
            if not self._computed:
                self._rest = self._compute_rest()
                self._computed = True
            return self._rest
        def __repr__(self):
            if self.empty:
                return '<empty stream>'
            return 'Stream({0}, <compute_rest>)'.format(repr(self.first))
>>> Stream.empty = Stream(None, None, True)

遞歸列表可使用嵌套表達式來定義。例如，我們可以創建RList，來表達1和5的序列，像下面這樣：

>>> r = Rlist(1, Rlist(2+3, Rlist.empty))

與之類似，我們可以創建一個Stream來表示相同序列。Stream在請求剩餘部分之前，並不會實際計算下一個元素5。

>>> s = Stream(1, lambda: Stream(2+3, lambda: Stream.empty))

這裡，1是流的第一個元素，後面的lambda表達式是用於計算流的剩餘部分的函數。被計算的流的第二個元素又是一個返回空流的函數。

訪問遞歸列表r和流s中的元素擁有相似的過程。但是，5儲存在了r之中，而對於s來說，它在首次被請求時通過加法來按要求計算。

>>> r.first
1
>>> s.first
1
>>> r.rest.first
5
>>> s.rest.first
5
>>> r.rest
Rlist(5)
>>> s.rest
Stream(5, <compute_rest>)

雖然 r 的 rest 是一個單元素遞歸列表，但 s 的其餘部分包括一個計算其餘部分的函數；它將返回空流的事實可能還沒有被發現。

當構造一個 Stream 實例時，字段 self._computed 為 False ，表示 Stream 的 _rest 還沒有被計算。當通過點表達式請求 rest 屬性時，會調用 rest 方法，以 self._rest = self.compute_rest 觸發計算。由於 Stream 中的緩存機制，compute_rest 函數只被調用一次。

compute_rest 函數的基本屬性是它不接受任何參數，並返回一個 Stream。

惰性求值使我們能夠用流來表示無限的順序數據集。例如，我們可以從任意 first 開始表示遞增的整數。

>>> def make_integer_stream(first=1):
      def compute_rest():
        return make_integer_stream(first+1)
      return Stream(first, compute_rest)
>>> ints = make_integer_stream()
>>> ints
Stream(1, <compute_rest>)
>>> ints.first
1

當make_integer_stream首次被調用時，它返回了一個流，流的first是序列中第一個整數（默認為1）。但是，make_integer_stream實際是遞歸的，因為這個流的compute_rest以自增的參數再次調用了make_integer_stream。這會讓make_integer_stream變成遞歸的，同時也是惰性的。

>>> ints.first
1
>>> ints.rest.first
2
>>> ints.rest.rest
Stream(3, <compute_rest>)

無論何時請求整數流的rest，都僅僅遞歸調用make_integer_stream。

操作序列的相同高階函數 -- map和filter -- 同樣可應用於流，雖然它們的實現必須修改來惰性調用它們的參數函數。map_stream在一個流上映射函數，這會產生一個新的流。局部定義的compute_rest函數確保了無論什麼時候rest被計算出來，這個函數都會在流的剩餘部分上映射。

>>> def map_stream(fn, s):
        if s.empty:
            return s
        def compute_rest():
            return map_stream(fn, s.rest)
        return Stream(fn(s.first), compute_rest)

流可以通過定義compute_rest函數來過濾，這個函數在流的剩餘部分上調用過濾器函數。如果過濾器函數拒絕了流的第一個元素，剩餘部分會立即計算出來。因為filter_stream是遞歸的，剩餘部分可能會多次計算直到找到了有效的first元素。

>>> def filter_stream(fn, s):
        if s.empty:
            return s
        def compute_rest():
            return filter_stream(fn, s.rest)
        if fn(s.first):
            return Stream(s.first, compute_rest)
        return compute_rest()

map_stream和filter_stream展示了流式處理的常見模式：無論流的剩餘部分何時被計算，局部定義的compute_rest函數都會對流的剩餘部分遞歸調用某個處理函數。

為了觀察流的內容，我們需要將其截斷為有限長度，並轉換為 Python list。

>>> def truncate_stream(s, k):
        if s.empty or k == 0:
            return Stream.empty
        def compute_rest():
            return truncate_stream(s.rest, k-1)
        return Stream(s.first, compute_rest)
>>> def stream_to_list(s):
        r = []
        while not s.empty:
            r.append(s.first)
            s = s.rest
        return r

這些便利的函數允許我們驗證map_stream的實現，使用一個非常簡單的例子，從3到7的整數平方。

>>> s = make_integer_stream(3)
>>> s
Stream(3, <compute_rest>)
>>> m = map_stream(lambda x: x*x, s)
>>> m
Stream(9, <compute_rest>)
>>> stream_to_list(truncate_stream(m, 5))
[9, 16, 25, 36, 49]

我們可以使用我們的filter_stream函數來定義素數流，使用埃拉託斯特尼篩法（sieve of Eratosthenes），它對整數流進行過濾，移除第一個元素的所有倍數數值。通過成功過濾出每個素數，所有合數都從流中移除了。

>>> def primes(pos_stream):
        def not_divible(x):
            return x % pos_stream.first != 0
        def compute_rest():
            return primes(filter_stream(not_divible, pos_stream.rest))
        return Stream(pos_stream.first, compute_rest)

通過截斷primes流，我們可以枚舉素數的任意前綴：

>>> p1 = primes(make_integer_stream(2))
>>> stream_to_list(truncate_stream(p1, 7))
[2, 3, 5, 7, 11, 13, 17]

流和迭代器不同，因為它們可以多次傳遞給純函數，並且每次都產生相同的值。素數流並沒有在轉換為列表之後“用完”。也就是說，在將流的前綴轉換為列表之後，p1的第一個元素仍舊是2。

>>> p1.first
2

就像遞歸列表提供了序列抽象的簡單實現，流提供了簡單、函數式的遞歸數據結構，它通過高階函數的使用實現了惰性求值。

5.3 協程

這篇文章的大部分專注於將複雜程序解構為小型、模塊化組件的技巧。當一個帶有複雜行為的函數邏輯劃分為幾個獨立的、本身為函數的步驟時，這些函數叫做輔助函數或者子過程。子過程由主函數調用，主函數負責協調子函數的使用。

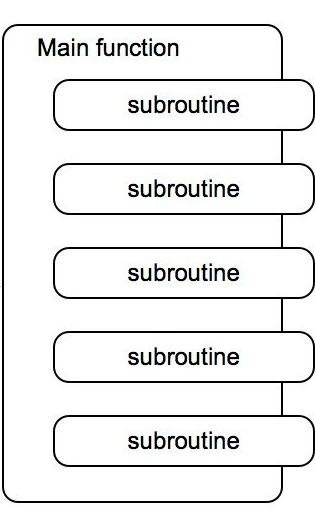
這一節中，我們使用協程，引入了一種不同的方式來解構複雜的計算。它是一種針對有序數據的任務處理方式。就像子過程那樣，協程會計算複雜計算的一小步。但是，在使用協程時，沒有主函數來協調結果。反之，協程會自發鏈接到一起來組成流水線。可能有一些協程消耗輸入數據，並把它發送到其它協程。也可能有一些協程，每個都對發送給它的數據執行簡單的處理步驟。最後可能有另外一些協程輸出最終結果。

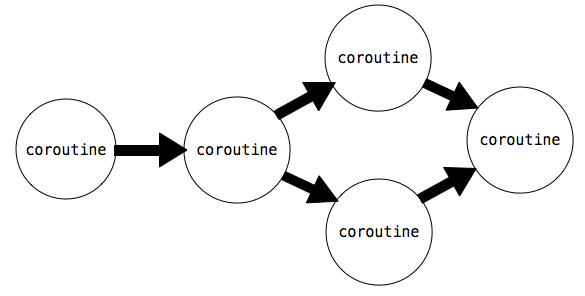
協程和子過程的差異是概念上的：子過程在主函數中位於下級，但是協程都是平等的，它們協作組成流水線，不帶有任何上級函數來負責以特定順序調用它們。

這一節中，我們會學到 Python 如何通過yield和send()語句來支持協程的構建。之後，我們會看到協程在流水線中的不同作用，以及協程如何支持多任務。

5.3.1 Python 協程

在之前一節中，我們介紹了生成器函數，它使用yield來返回一個值。Python 的生成器函數也可以使用(yield)語句來接受一個值。生成器對象上有兩個額外的方法：send()和close()，創建了一個模型使對象可以消耗或產出值。定義了這些對象的生成器函數叫做協程。

協程可以通過(yield)語句來消耗值，向像下面這樣：

value = (yield)

使用這個語法，在帶參數調用對象的send方法之前，執行流會停留在這條語句上。

coroutine.send(data)

之後，執行會恢復，value會被賦為data的值。為了發射計算終止的信號，我們需要使用close()方法來關閉協程。這會在協程內部產生GeneratorExit異常，它可以由try/except子句來捕獲。

下面的例子展示了這些概念。它是一個協程，用於打印匹配所提供的模式串的字符串。

>>> def match(pattern):
        print('Looking for ' + pattern)
        try:
            while True:
                s = (yield)
                if pattern in s:
                    print(s)
        except GeneratorExit:
            print("=== Done ===")

我們可以使用一個模式串來初始化它，之後調用__next__()來開始執行：

>>> m = match("Jabberwock")
>>> m.__next__()
Looking for Jabberwock

對__next__()的調用會執行函數體，所以"Looking for jabberwock"會被打印。語句會一直持續執行，直到遇到line = (yield)語句。之後，執行會暫停，並且等待一個發送給m的值。我們可以使用send來將值發送給它。

>>> m.send("the Jabberwock with eyes of flame")
the Jabberwock with eyes of flame
>>> m.send("came whiffling through the tulgey wood")
>>> m.send("and burbled as it came")
>>> m.close()
=== Done ===

當我們以一個值調用m.send時，協程m內部的求值會在line = (yield)語句處恢復，這裡會把發送的值賦給line變量。m中的語句會繼續求值，如果匹配的話會打印出那一行，並繼續執行循環，直到再次進入line = (yield)。之後，m中的求值會暫停，並在m.send調用後恢復。

我們可以將使用send()和yield的函數鏈到一起來完成複雜的行為。例如，下面的函數將名為text的字符串分割為單詞，並把每個單詞發送給另一個協程。

每個單詞都發送給了綁定到next_coroutine的協程，使next_coroutine開始執行，而且這個函數暫停並等待。它在next_coroutine暫停之前會一直等待，隨後這個函數恢復執行，發送下一個單詞或執行完畢。

如果我們將上面定義的match和這個函數鏈到一起，我們就可以創建出一個程序，只打印出匹配特定單詞的單詞。

>>> text = 'Commending spending is offending to people pending lending!'
>>> matcher = match('ending')
>>> matcher.__next__()
Looking for ending
>>> read(text, matcher)
Commending
spending
offending
pending
lending!
=== Done ===

read函數向協程matcher發送每個單詞，協程打印出任何匹配pattern的輸入。在matcher協程中，s = (yield)一行等待每個發送進來的單詞，並且在執行到這一行之後將控制流交還給read。

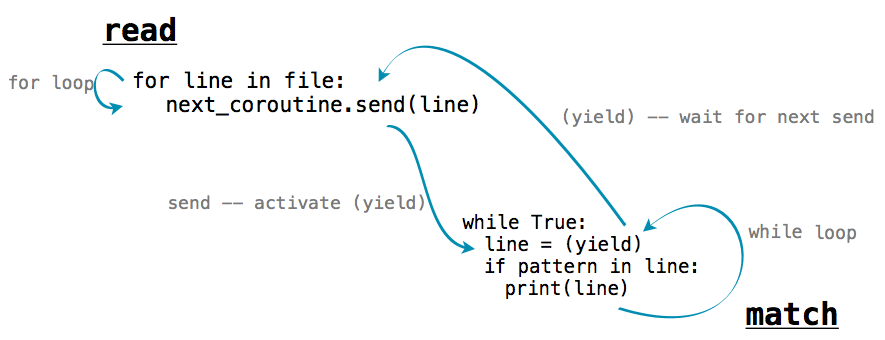
5.3.2 生產、過濾和消耗

協程基於如何使用yield和send()而具有不同的作用：

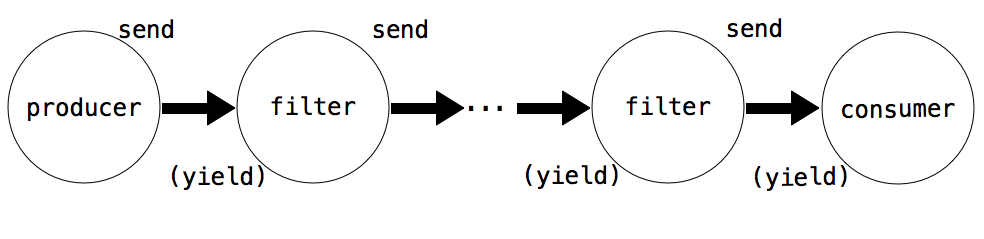
• 生產者創建序列中的物品，並使用send()，而不是(yield)。
• 過濾器使用(yield)來消耗物品並將結果使用send()發送給下一個步驟。
• 消費者使用(yield)來消耗物品，但是從不發送。

上面的read函數是一個生產者的例子。它不使用(yield)，但是使用send來生產數據。函數match是個消費者的例子。它不使用send發送任何東西，但是使用(yield)來消耗數據。我們可以將match拆分為過濾器和消費者。過濾器是一個協程，只發送與它的模式相匹配的字符串。

>>> def match_filter(pattern, next_coroutine):
        print('Looking for ' + pattern)
        try:
            while True:
                s = (yield)
                if pattern in s:
                    next_coroutine.send(s)
        except GeneratorExit:
            next_coroutine.close()

消費者是一個函數，只打印出發送給它的行：

>>> def print_consumer():
        print('Preparing to print')
        try:
            while True:
                line = (yield)
                print(line)
        except GeneratorExit:
            print("=== Done ===")

當過濾器或消費者被構建時，必須調用它的__next__方法來開始執行：

>>> printer = print_consumer()
>>> printer.__next__()
Preparing to print
>>> matcher = match_filter('pend', printer)
>>> matcher.__next__()
Looking for pend
>>> read(text, matcher)
spending
pending
=== Done ===

即使名稱filter暗示移除元素，過濾器也可以轉換元素。下面的函數是個轉換元素的過濾器的示例。它消耗字符串併發送一個字典，包含了每個不同的字母在字符串中的出現次數。

>>> def count_letters(next_coroutine):
        try:
            while True:
                s = (yield)
                counts = {letter:s.count(letter) for letter in set(s)}
                next_coroutine.send(counts)
        except GeneratorExit as e:
            next_coroutine.close()

我們可以使用它來計算文本中最常出現的字母，並使用一個消費者，將字典合併來找出最常出現的鍵。

>>> def sum_dictionaries():
        total = {}
        try:
            while True:
                counts = (yield)
                for letter, count in counts.items():
                    total[letter] = count + total.get(letter, 0)
        except GeneratorExit:
            max_letter = max(total.items(), key=lambda t: t[1])[0]
            print("Most frequent letter: " + max_letter)

為了在文件上運行這個流水線，我們必須首先按行讀取文件。之後，將結果發送給count_letters，最後發送給sum_dictionaries。我們可以服用read協程來讀取文件中的行。

>>> s = sum_dictionaries()
>>> s.__next__()
>>> c = count_letters(s)
>>> c.__next__()
>>> read(text, c)
Most frequent letter: n

5.3.3 多任務

生產者或過濾器並不受限於唯一的下游。它可以擁有多個協程作為它的下游，並使用send()向它們發送數據。例如，下面是read的一個版本，向多個下游發送字符串中的單詞：

>>> def read_to_many(text, coroutines):
        for word in text.split():
            for coroutine in coroutines:
                coroutine.send(word)
        for coroutine in coroutines:
            coroutine.close()

我們可以使用它來檢測多個單詞中的相同文本：

>>> m = match("mend")
>>> m.__next__()
Looking for mend
>>> p = match("pe")
>>> p.__next__()
Looking for pe
>>> read_to_many(text, [m, p])
Commending
spending
people
pending
=== Done ===
=== Done ===

首先，read_to_many在m上調用了send(word)。這個協程正在等待循環中的text = (yield)，之後打印出所發現的匹配，並且等待下一個send。之後執行流返回到了read_to_many，它向p發送相同的行。所以，text中的單詞會按照順序打印出來。

5.1 引言

在這一章中，我們通過開發新的工具來處理有序數據，繼續討論真實世界中的應用。在第二章中，我們介紹了序列接口，在 Python 內置的數據類型例如tuple和list中實現。序列支持兩個操作：獲取長度和由下標訪問元素。第三章中，我們開發了序列接口的用戶定義實現，用於表示遞歸列表的Rlist類。序列類型具有高效的表現力，並且可以讓我們高效訪問大量有序數據集。

但是，使用序列抽象表示有序數據有兩個重要限制。第一個是長度為n的序列的要佔據比例為n的內存總數。於是，序列越長，表示它所佔的內存空間就越大。

第二個限制是，序列只能表示已知且長度有限的數據集。許多我們想要表示的有序集合並沒有定義好的長度，甚至有些是無限的。兩個無限序列的數學示例是正整數和斐波那契數。無限長度的有序數據集也出現在其它計算領域，例如，所有推特狀態的序列每秒都在增長，所以並沒有固定的長度。與之類似，經過基站發送出的電話呼叫序列，由計算機用戶發出的鼠標動作序列，以及飛機上的傳感器產生的加速度測量值序列，都在世界演化過程中無限擴展。

在這一章中，我們介紹了新的構造方式用於處理有序數據，它為容納未知或無限長度的集合而設計，但僅僅使用有限的內存。我們也會討論這些工具如何用於一種叫做協程的程序結構，來創建高效、模塊化的數據處理流水線。

5.2 隱式序列

序列可以使用一種程序結構來表示，它不將每個元素顯式儲存在內存中，這是高效處理有序數據的核心概念。為了將這個概念用於實踐，我們需要構造對象來提供序列中所有元素的訪問，但是不要事先把所有元素計算出來並儲存。

這個概念的一個簡單示例就是第二章出現的range序列類型。range表示連續有界的整數序列。但是，它的每個元素並不顯式在內存中表示，當元素從range中獲取時，才被計算出來。所以，我們可以表示非常大的整數範圍。只有範圍的結束位置才被儲存為range對象的一部分，元素都被憑空計算出來。

>>> r = range(10000, 1000000000)
>>> r[45006230]
45016230

這個例子中，當構造範圍示例時，並不是這個範圍內的所有 999,990,000 個整數都被儲存。反之，範圍對象將第一個元素 10,000 與下標相加 45,006,230 來產生第 45,016,230 個元素。計算所求的元素值並不從現有的表示中獲取，這是惰性計算的一個例子。計算機科學將惰性作為一種重要的計算工具加以讚揚。

迭代器是提供底層有序數據集的有序訪問的對象。迭代器在許多編程語言中都是內建對象，包括 Python。迭代器抽象擁有兩個組成部分：一種獲取底層元素序列的下一個元素的機制，以及一種標識元素序列已經到達末尾，沒有更多剩餘元素的機制。在帶有內建對象系統的編程語言中，這個抽象通常相當於可以由類實現的特定接口。Python 的迭代器接口會在下一節中描述。

迭代器的實用性來源於一個事實，底層數據序列並不能顯式在內存中表達。迭代器提供了一種機制，可以依次計算序列中的每個值，但是所有元素不需要連續儲存。反之，當下個元素從迭代器獲取的時候，這個元素會按照請求計算，而不是從現有的內存來源中獲取。

範圍可以惰性計算序列中的元素，因為序列的表示是統一的，並且任何元素都可以輕易從範圍的起始和結束位置計算出來。迭代器支持更廣泛的底層有序數據集的惰性生成，因為它們不需要提供底層序列任意元素的訪問途徑。反之，它們僅僅需要按照順序，在每次其它元素被請求的時候，計算出序列的下一個元素。雖然不像序列可訪問任意元素那樣靈活（叫做隨機訪問），有序數據序列的順序訪問對於數據處理應用來說已經足夠了。

5.2.1 Python 迭代器

Python 迭代器接口包含兩個消息。__next__消息向迭代器獲取所表示的底層序列的下一個元素。為了對__next__方法調用做出回應，迭代器可以執行任何計算來獲取或計算底層數據序列的下一個元素。__next__的調用讓迭代器產生變化：它們向前移動迭代器的位置。所以多次調用__next__會有序返回底層序列的元素。在__next__的調用過程中，Python 通過StopIteration異常，來表示底層數據序列已經到達末尾。

下面的Letters類迭代了從a到d字母的底層序列。成員變量current儲存了序列中的當前字母。__next__方法返回這個字母，並且使用它來計算current的新值。

>>> class Letters(object):
        def __init__(self):
            self.current = 'a'
        def __next__(self):
            if self.current > 'd':
                raise StopIteration
            result = self.current
            self.current = chr(ord(result)+1)
            return result
        def __iter__(self):
            return self

__iter__消息是 Python 迭代器所需的第二個消息。它只是簡單返回迭代器，它對於提供迭代器和序列的通用接口很有用，在下一節會描述。

使用這個類，我們就可以訪問序列中的字母：

>>> letters = Letters()
>>> letters.__next__()
'a'
>>> letters.__next__()
'b'
>>> letters.__next__()
'c'
>>> letters.__next__()
'd'
>>> letters.__next__()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 12, in next
StopIteration

Letters示例只能迭代一次。一旦__next__()方法產生了StopIteration異常，它就從此之後一直這樣了。除非創建新的實例，否則沒有辦法來重置它。

迭代器也允許我們表示無限序列，通過實現永遠不會產生StopIteration異常的__next__方法。例如，下面展示的Positives類迭代了正整數的無限序列：

>>> class Positives(object):
        def __init__(self):
            self.current = 0;
        def __next__(self):
            result = self.current
            self.current += 1
            return result
        def __iter__(self):
            return self

5.2.2 for語句

Python 中，序列可以通過實現__iter__消息用於迭代。如果一個對象表示有序數據，它可以在for語句中用作可迭代對象，通過回應__iter__消息來返回迭代器。這個迭代器應擁有__next__()方法，依次返回序列中的每個元素，最後到達序列末尾時產生StopIteration異常。

>>> counts = [1, 2, 3]
>>> for item in counts:
        print(item)
1
2
3

在上面的實例中，counts列表返回了迭代器，作為__iter__()方法調用的回應。for語句之後反覆調用迭代器的__next__()方法，並且每次都將返回值賦給item。這個過程一直持續，直到迭代器產生了StopIteration異常，這時for語句就終止了。

使用我們關於迭代器的知識，我們可以拿while、賦值和try語句實現for語句的求值規則：

>>> i = counts.__iter__()
>>> try:
        while True:
            item = i.__next__()
            print(item)
    except StopIteration:
        pass
1
2
3

在上面，調用counts的__iter__方法所返回的迭代器綁定到了名稱i上面，便於依次獲取每個元素。StopIteration異常的處理子句不做任何事情，但是這個異常的處理提供了退出while循環的控制機制。

5.2.3 生成器和yield語句

上面的Letters和Positives對象需要我們引入一種新的字段，self.current，來跟蹤序列的處理過程。在上面所示的簡單序列中，這可以輕易實現。但對於複雜序列，__next__()很難在計算中節省空間。生成器允許我們通過利用 Python 解釋器的特性定義更復雜的迭代。

生成器是由一類特殊函數，叫做生成器函數返回的迭代器。生成器函數不同於普通的函數，因為它不在函數體中包含return語句，而是使用yield語句來返回序列中的元素。

生成器不使用任何對象屬性來跟蹤序列的處理過程。它們控制生成器函數的執行，每次__next__方法調用時，它們執行到下一個yield語句。Letters迭代可以使用生成器函數實現得更加簡潔。

>>> def letters_generator():
        current = 'a'
        while current <= 'd':
            yield current
            current = chr(ord(current)+1)
>>> for letter in letters_generator():
        print(letter)
a
b
c
d

即使我們永不顯式定義__iter__()或__next__()方法，Python 會理解當我們使用yield語句時，我們打算定義生成器函數。調用時，生成器函數並不返回特定的產出值，而是返回一個生成器（一種迭代器），它自己就可以返回產出的值。生成器對象擁有__iter__和__next__方法，每個對__next__的調用都會從上次停留的地方繼續執行生成器函數，直到另一個yield語句執行的地方。

__next__第一次調用時，程序從letters_generator的函數體一直執行到進入yield語句。之後，它暫停並返回current值。yield語句並不破壞新創建的環境，而是為之後的使用保留了它。當__next__再次調用時，執行在它停留的地方恢復。letters_generator作用域中current和任何所綁定名稱的值都會在隨後的__next__調用中保留。

我們可以通過手動調用__next__()來遍歷生成器：

>>> letters = letters_generator()
>>> type(letters)
<class 'generator'>
>>> letters.__next__()
'a'
>>> letters.__next__()
'b'
>>> letters.__next__()
'c'
>>> letters.__next__()
'd'
>>> letters.__next__()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
StopIteration

在第一次__next__()調用之前，生成器並不會開始執行任何生成器函數體中的語句。

5.2.4 可迭代對象

Python 中，迭代只會遍歷一次底層序列的元素。在遍歷之後，迭代器在__next__()調用時會產生StopIteration異常。許多應用需要迭代多次元素。例如，我們需要對一個列表迭代多次來枚舉所有的元素偶對：

>>> def all_pairs(s):
        for item1 in s:
            for item2 in s:
                yield (item1, item2)
>>> list(all_pairs([1, 2, 3]))
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]

序列本身不是迭代器，但是它是可迭代對象。Python 的可迭代接口只包含一個消息，__iter__，返回一個迭代器。Python 中內建的序列類型在__iter__方法調用時，返回迭代器的新實例。如果一個可迭代對象在每次調用__iter__時返回了迭代器的新實例，那麼它就能被迭代多次。

新的可迭代類可以通過實現可迭代接口來定義。例如，下面的可迭代對象LetterIterable類在每次調用__iter__時返回新的迭代器來迭代字母。

>>> class LetterIterable(object):
        def __iter__(self):
            current = 'a'
            while current <= 'd':
                yield current
                current = chr(ord(current)+1)

__iter__方法是個生成器函數，它返回一個生成器對象，產出從'a'到'd'的字母。

Letters迭代器對象在單次迭代之後就被“用完”了，但是LetterIterable對象可被迭代多次。所以，LetterIterable示例可以用於all_pairs的參數。

>>> letters = LetterIterable()
>>> all_pairs(letters).__next__()
('a', 'a')

5.2.5 流

流提供了一種隱式表示有序數據的最終方式。流是惰性計算的遞歸列表。就像第三章的Rlist類那樣，Stream實例可以響應對其第一個元素和剩餘部分的獲取請求。同樣，Stream的剩餘部分還是Stream。然而不像RList，流的剩餘部分只在查找時被計算，而不是事先存儲。也就是說流的剩餘部分是惰性計算的。

為了完成這個惰性求值，流會儲存計算剩餘部分的函數。無論這個函數在什麼時候調用，它的返回值都作為流的一部分，儲存在叫做_rest的屬性中。下劃線表示它不應直接訪問。可訪問的屬性rest是個方法，它返回流的剩餘部分，並在必要時計算它。使用這個設計，流可以儲存計算剩餘部分的方式，而不用總是顯式儲存它們。

>>> class Stream(object):
        """A lazily computed recursive list."""
        def __init__(self, first, compute_rest, empty=False):
            self.first = first
            self._compute_rest = compute_rest
            self.empty = empty
            self._rest = None
            self._computed = False
        @property
        def rest(self):
            """Return the rest of the stream, computing it if necessary."""
            assert not self.empty, 'Empty streams have no rest.'
            if not self._computed:
                self._rest = self._compute_rest()
                self._computed = True
            return self._rest
        def __repr__(self):
            if self.empty:
                return '<empty stream>'
            return 'Stream({0}, <compute_rest>)'.format(repr(self.first))
>>> Stream.empty = Stream(None, None, True)

遞歸列表可使用嵌套表達式來定義。例如，我們可以創建RList，來表達1和5的序列，像下面這樣：

>>> r = Rlist(1, Rlist(2+3, Rlist.empty))

與之類似，我們可以創建一個Stream來表示相同序列。Stream在請求剩餘部分之前，並不會實際計算下一個元素5。

>>> s = Stream(1, lambda: Stream(2+3, lambda: Stream.empty))

這裡，1是流的第一個元素，後面的lambda表達式是用於計算流的剩餘部分的函數。被計算的流的第二個元素又是一個返回空流的函數。

訪問遞歸列表r和流s中的元素擁有相似的過程。但是，5儲存在了r之中，而對於s來說，它在首次被請求時通過加法來按要求計算。

>>> r.first
1
>>> s.first
1
>>> r.rest.first
5
>>> s.rest.first
5
>>> r.rest
Rlist(5)
>>> s.rest
Stream(5, <compute_rest>)

雖然 r 的 rest 是一個單元素遞歸列表，但 s 的其餘部分包括一個計算其餘部分的函數；它將返回空流的事實可能還沒有被發現。

當構造一個 Stream 實例時，字段 self._computed 為 False ，表示 Stream 的 _rest 還沒有被計算。當通過點表達式請求 rest 屬性時，會調用 rest 方法，以 self._rest = self.compute_rest 觸發計算。由於 Stream 中的緩存機制，compute_rest 函數只被調用一次。

compute_rest 函數的基本屬性是它不接受任何參數，並返回一個 Stream。

惰性求值使我們能夠用流來表示無限的順序數據集。例如，我們可以從任意 first 開始表示遞增的整數。

>>> def make_integer_stream(first=1):
      def compute_rest():
        return make_integer_stream(first+1)
      return Stream(first, compute_rest)
>>> ints = make_integer_stream()
>>> ints
Stream(1, <compute_rest>)
>>> ints.first
1

當make_integer_stream首次被調用時，它返回了一個流，流的first是序列中第一個整數（默認為1）。但是，make_integer_stream實際是遞歸的，因為這個流的compute_rest以自增的參數再次調用了make_integer_stream。這會讓make_integer_stream變成遞歸的，同時也是惰性的。

>>> ints.first
1
>>> ints.rest.first
2
>>> ints.rest.rest
Stream(3, <compute_rest>)

無論何時請求整數流的rest，都僅僅遞歸調用make_integer_stream。

操作序列的相同高階函數 -- map和filter -- 同樣可應用於流，雖然它們的實現必須修改來惰性調用它們的參數函數。map_stream在一個流上映射函數，這會產生一個新的流。局部定義的compute_rest函數確保了無論什麼時候rest被計算出來，這個函數都會在流的剩餘部分上映射。

>>> def map_stream(fn, s):
        if s.empty:
            return s
        def compute_rest():
            return map_stream(fn, s.rest)
        return Stream(fn(s.first), compute_rest)

流可以通過定義compute_rest函數來過濾，這個函數在流的剩餘部分上調用過濾器函數。如果過濾器函數拒絕了流的第一個元素，剩餘部分會立即計算出來。因為filter_stream是遞歸的，剩餘部分可能會多次計算直到找到了有效的first元素。

>>> def filter_stream(fn, s):
        if s.empty:
            return s
        def compute_rest():
            return filter_stream(fn, s.rest)
        if fn(s.first):
            return Stream(s.first, compute_rest)
        return compute_rest()

map_stream和filter_stream展示了流式處理的常見模式：無論流的剩餘部分何時被計算，局部定義的compute_rest函數都會對流的剩餘部分遞歸調用某個處理函數。

為了觀察流的內容，我們需要將其截斷為有限長度，並轉換為 Python list。

>>> def truncate_stream(s, k):
        if s.empty or k == 0:
            return Stream.empty
        def compute_rest():
            return truncate_stream(s.rest, k-1)
        return Stream(s.first, compute_rest)
>>> def stream_to_list(s):
        r = []
        while not s.empty:
            r.append(s.first)
            s = s.rest
        return r

這些便利的函數允許我們驗證map_stream的實現，使用一個非常簡單的例子，從3到7的整數平方。

>>> s = make_integer_stream(3)
>>> s
Stream(3, <compute_rest>)
>>> m = map_stream(lambda x: x*x, s)
>>> m
Stream(9, <compute_rest>)
>>> stream_to_list(truncate_stream(m, 5))
[9, 16, 25, 36, 49]

我們可以使用我們的filter_stream函數來定義素數流，使用埃拉託斯特尼篩法（sieve of Eratosthenes），它對整數流進行過濾，移除第一個元素的所有倍數數值。通過成功過濾出每個素數，所有合數都從流中移除了。

>>> def primes(pos_stream):
        def not_divible(x):
            return x % pos_stream.first != 0
        def compute_rest():
            return primes(filter_stream(not_divible, pos_stream.rest))
        return Stream(pos_stream.first, compute_rest)

通過截斷primes流，我們可以枚舉素數的任意前綴：

>>> p1 = primes(make_integer_stream(2))
>>> stream_to_list(truncate_stream(p1, 7))
[2, 3, 5, 7, 11, 13, 17]

流和迭代器不同，因為它們可以多次傳遞給純函數，並且每次都產生相同的值。素數流並沒有在轉換為列表之後“用完”。也就是說，在將流的前綴轉換為列表之後，p1的第一個元素仍舊是2。

>>> p1.first
2

就像遞歸列表提供了序列抽象的簡單實現，流提供了簡單、函數式的遞歸數據結構，它通過高階函數的使用實現了惰性求值。

5.3 協程

這篇文章的大部分專注於將複雜程序解構為小型、模塊化組件的技巧。當一個帶有複雜行為的函數邏輯劃分為幾個獨立的、本身為函數的步驟時，這些函數叫做輔助函數或者子過程。子過程由主函數調用，主函數負責協調子函數的使用。

這一節中，我們使用協程，引入了一種不同的方式來解構複雜的計算。它是一種針對有序數據的任務處理方式。就像子過程那樣，協程會計算複雜計算的一小步。但是，在使用協程時，沒有主函數來協調結果。反之，協程會自發鏈接到一起來組成流水線。可能有一些協程消耗輸入數據，並把它發送到其它協程。也可能有一些協程，每個都對發送給它的數據執行簡單的處理步驟。最後可能有另外一些協程輸出最終結果。

協程和子過程的差異是概念上的：子過程在主函數中位於下級，但是協程都是平等的，它們協作組成流水線，不帶有任何上級函數來負責以特定順序調用它們。

這一節中，我們會學到 Python 如何通過yield和send()語句來支持協程的構建。之後，我們會看到協程在流水線中的不同作用，以及協程如何支持多任務。

5.3.1 Python 協程

在之前一節中，我們介紹了生成器函數，它使用yield來返回一個值。Python 的生成器函數也可以使用(yield)語句來接受一個值。生成器對象上有兩個額外的方法：send()和close()，創建了一個模型使對象可以消耗或產出值。定義了這些對象的生成器函數叫做協程。

協程可以通過(yield)語句來消耗值，向像下面這樣：

value = (yield)

使用這個語法，在帶參數調用對象的send方法之前，執行流會停留在這條語句上。

coroutine.send(data)

之後，執行會恢復，value會被賦為data的值。為了發射計算終止的信號，我們需要使用close()方法來關閉協程。這會在協程內部產生GeneratorExit異常，它可以由try/except子句來捕獲。

下面的例子展示了這些概念。它是一個協程，用於打印匹配所提供的模式串的字符串。

>>> def match(pattern):
        print('Looking for ' + pattern)
        try:
            while True:
                s = (yield)
                if pattern in s:
                    print(s)
        except GeneratorExit:
            print("=== Done ===")

我們可以使用一個模式串來初始化它，之後調用__next__()來開始執行：

>>> m = match("Jabberwock")
>>> m.__next__()
Looking for Jabberwock

對__next__()的調用會執行函數體，所以"Looking for jabberwock"會被打印。語句會一直持續執行，直到遇到line = (yield)語句。之後，執行會暫停，並且等待一個發送給m的值。我們可以使用send來將值發送給它。

>>> m.send("the Jabberwock with eyes of flame")
the Jabberwock with eyes of flame
>>> m.send("came whiffling through the tulgey wood")
>>> m.send("and burbled as it came")
>>> m.close()
=== Done ===

當我們以一個值調用m.send時，協程m內部的求值會在line = (yield)語句處恢復，這裡會把發送的值賦給line變量。m中的語句會繼續求值，如果匹配的話會打印出那一行，並繼續執行循環，直到再次進入line = (yield)。之後，m中的求值會暫停，並在m.send調用後恢復。

我們可以將使用send()和yield的函數鏈到一起來完成複雜的行為。例如，下面的函數將名為text的字符串分割為單詞，並把每個單詞發送給另一個協程。

每個單詞都發送給了綁定到next_coroutine的協程，使next_coroutine開始執行，而且這個函數暫停並等待。它在next_coroutine暫停之前會一直等待，隨後這個函數恢復執行，發送下一個單詞或執行完畢。

如果我們將上面定義的match和這個函數鏈到一起，我們就可以創建出一個程序，只打印出匹配特定單詞的單詞。

>>> text = 'Commending spending is offending to people pending lending!'
>>> matcher = match('ending')
>>> matcher.__next__()
Looking for ending
>>> read(text, matcher)
Commending
spending
offending
pending
lending!
=== Done ===

read函數向協程matcher發送每個單詞，協程打印出任何匹配pattern的輸入。在matcher協程中，s = (yield)一行等待每個發送進來的單詞，並且在執行到這一行之後將控制流交還給read。

5.3.2 生產、過濾和消耗

協程基於如何使用yield和send()而具有不同的作用：

• 生產者創建序列中的物品，並使用send()，而不是(yield)。
• 過濾器使用(yield)來消耗物品並將結果使用send()發送給下一個步驟。
• 消費者使用(yield)來消耗物品，但是從不發送。

上面的read函數是一個生產者的例子。它不使用(yield)，但是使用send來生產數據。函數match是個消費者的例子。它不使用send發送任何東西，但是使用(yield)來消耗數據。我們可以將match拆分為過濾器和消費者。過濾器是一個協程，只發送與它的模式相匹配的字符串。

>>> def match_filter(pattern, next_coroutine):
        print('Looking for ' + pattern)
        try:
            while True:
                s = (yield)
                if pattern in s:
                    next_coroutine.send(s)
        except GeneratorExit:
            next_coroutine.close()

消費者是一個函數，只打印出發送給它的行：

>>> def print_consumer():
        print('Preparing to print')
        try:
            while True:
                line = (yield)
                print(line)
        except GeneratorExit:
            print("=== Done ===")

當過濾器或消費者被構建時，必須調用它的__next__方法來開始執行：

>>> printer = print_consumer()
>>> printer.__next__()
Preparing to print
>>> matcher = match_filter('pend', printer)
>>> matcher.__next__()
Looking for pend
>>> read(text, matcher)
spending
pending
=== Done ===

即使名稱filter暗示移除元素，過濾器也可以轉換元素。下面的函數是個轉換元素的過濾器的示例。它消耗字符串併發送一個字典，包含了每個不同的字母在字符串中的出現次數。

>>> def count_letters(next_coroutine):
        try:
            while True:
                s = (yield)
                counts = {letter:s.count(letter) for letter in set(s)}
                next_coroutine.send(counts)
        except GeneratorExit as e:
            next_coroutine.close()

我們可以使用它來計算文本中最常出現的字母，並使用一個消費者，將字典合併來找出最常出現的鍵。

>>> def sum_dictionaries():
        total = {}
        try:
            while True:
                counts = (yield)
                for letter, count in counts.items():
                    total[letter] = count + total.get(letter, 0)
        except GeneratorExit:
            max_letter = max(total.items(), key=lambda t: t[1])[0]
            print("Most frequent letter: " + max_letter)

為了在文件上運行這個流水線，我們必須首先按行讀取文件。之後，將結果發送給count_letters，最後發送給sum_dictionaries。我們可以服用read協程來讀取文件中的行。

>>> s = sum_dictionaries()
>>> s.__next__()
>>> c = count_letters(s)
>>> c.__next__()
>>> read(text, c)
Most frequent letter: n

5.3.3 多任務

生產者或過濾器並不受限於唯一的下游。它可以擁有多個協程作為它的下游，並使用send()向它們發送數據。例如，下面是read的一個版本，向多個下游發送字符串中的單詞：

>>> def read_to_many(text, coroutines):
        for word in text.split():
            for coroutine in coroutines:
                coroutine.send(word)
        for coroutine in coroutines:
            coroutine.close()

我們可以使用它來檢測多個單詞中的相同文本：

>>> m = match("mend")
>>> m.__next__()
Looking for mend
>>> p = match("pe")
>>> p.__next__()
Looking for pe
>>> read_to_many(text, [m, p])
Commending
spending
people
pending
=== Done ===
=== Done ===

首先，read_to_many在m上調用了send(word)。這個協程正在等待循環中的text = (yield)，之後打印出所發現的匹配，並且等待下一個send。之後執行流返回到了read_to_many，它向p發送相同的行。所以，text中的單詞會按照順序打印出來。