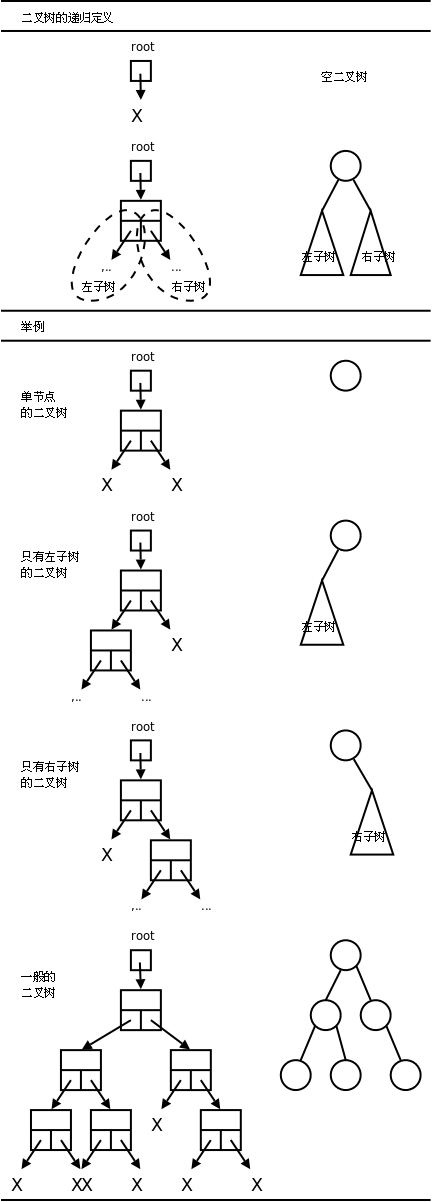
鏈表的每個節點可以有一個後繼,而二叉樹(Binary Tree)的每個節點可以有兩個後繼。比如這樣定義二叉樹的節點:
typedef struct node *link;
struct node {
unsigned char item;
link l, r;
};這樣的節點可以組織成下圖所示的各種形態。
二叉樹可以這樣遞歸地定義:
就像鏈表有頭指針一樣,每個二叉樹都有一個根指針(上圖中的
root指針)指向它。根指針可以是NULL,表示空二叉樹,或者根指針可以指向一個節點,這個節點除了有數據成員之外還有兩個指針域,這兩個指針域又分別是另外兩個二叉樹(左子樹和右子樹)的根指針。
上圖舉例示意了幾種情況。
單節點的二叉樹:左子樹和右子樹都是空二叉樹。
只有左子樹的二叉樹:右子樹是空二叉樹。
只有右子樹的二叉樹:左子樹是空二叉樹。
一般的二叉樹:左右子樹都不為空。注意右側由圈和線段組成的簡化圖示,以後我們都採用這種簡化圖示法,在圈中標上該節點數據成員的值。
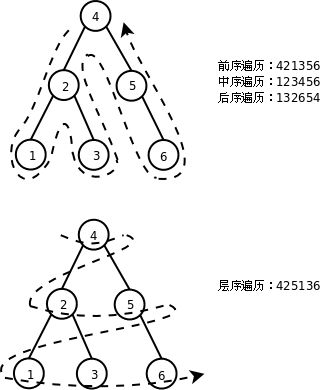
鏈表的遍歷方法是顯而易見的:從前到後遍歷即可。二叉樹是一種樹狀結構,如何做到把所有節點都走一遍不重不漏呢?有以下幾種方法:
前序(Pre-order Traversal)、中序(In-order Traversal)、後序遍歷(Post-order Traversal)和深度優先搜索的順序類似,層序遍歷(Level-order Traversal)和廣度優先搜索的順序類似。
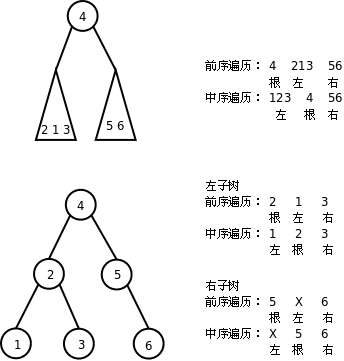
前序和中序遍歷的結果合在一起可以唯一確定二叉樹的形態,也就是說根據遍歷結果可以構造出二叉樹。過程如下圖所示:
想一想,根據中序和後序遍歷結果能否構造二叉樹?根據前序和後序遍歷結果能否構造二叉樹?
例 26.3. 二叉樹
/* binarytree.h */
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef struct node *link;
struct node {
unsigned char item;
link l, r;
};
link init(unsigned char VLR[], unsigned char LVR[], int n);
void pre_order(link t, void (*visit)(link));
void in_order(link t, void (*visit)(link));
void post_order(link t, void (*visit)(link));
int count(link t);
int depth(link t);
void destroy(link t);
#endif/* binarytree.c */
#include <stdlib.h>
#include "binarytree.h"
static link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->l = p->r = NULL;
return p;
}
static void free_node(link p)
{
free(p);
}
link init(unsigned char VLR[], unsigned char LVR[], int n)
{
link t;
int k;
if (n <= 0)
return NULL;
for (k = 0; VLR[0] != LVR[k]; k++);
t = make_node(VLR[0]);
t->l = init(VLR+1, LVR, k);
t->r = init(VLR+1+k, LVR+1+k, n-k-1);
return t;
}
void pre_order(link t, void (*visit)(link))
{
if (!t)
return;
visit(t);
pre_order(t->l, visit);
pre_order(t->r, visit);
}
void in_order(link t, void (*visit)(link))
{
if (!t)
return;
in_order(t->l, visit);
visit(t);
in_order(t->r, visit);
}
void post_order(link t, void (*visit)(link))
{
if (!t)
return;
post_order(t->l, visit);
post_order(t->r, visit);
visit(t);
}
int count(link t)
{
if (!t)
return 0;
return 1 + count(t->l) + count(t->r);
}
int depth(link t)
{
int dl, dr;
if (!t)
return 0;
dl = depth(t->l);
dr = depth(t->r);
return 1 + (dl > dr ? dl : dr);
}
void destroy(link t)
{
post_order(t, free_node);
}/* main.c */
#include <stdio.h>
#include "binarytree.h"
void print_item(link p)
{
printf("%d", p->item);
}
int main()
{
unsigned char pre_seq[] = { 4, 2, 1, 3, 6, 5, 7 };
unsigned char in_seq[] = { 1, 2, 3, 4, 5, 6, 7 };
link root = init(pre_seq, in_seq, 7);
pre_order(root, print_item);
putchar('\n');
in_order(root, print_item);
putchar('\n');
post_order(root, print_item);
putchar('\n');
printf("count=%d depth=%d\n", count(root), depth(root));
destroy(root);
return 0;
}排序二叉樹(BST,Binary Search Tree)具有這樣的性質:對於二叉樹中的任意節點,如果它有左子樹或右子樹,則該節點的數據成員大於左子樹所有節點的數據成員,且小於右子樹所有節點的數據成員。排序二叉樹的中序遍歷結果是從小到大排列的,其實上一節的圖 26.10 “二叉樹的遍歷”就是排序二叉樹。
例 26.4. 排序二叉樹
/* bst.h */
#ifndef BST_H
#define BST_H
typedef struct node *link;
struct node {
unsigned char item;
link l, r;
};
link search(link t, unsigned char key);
link insert(link t, unsigned char key);
link delete(link t, unsigned char key);
void print_tree(link t);
#endif/* bst.c */
#include <stdlib.h>
#include <stdio.h>
#include "bst.h"
static link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->l = p->r = NULL;
return p;
}
static void free_node(link p)
{
free(p);
}
link search(link t, unsigned char key)
{
if (!t)
return NULL;
if (t->item > key)
return search(t->l, key);
if (t->item < key)
return search(t->r, key);
/* if (t->item == key) */
return t;
}
link insert(link t, unsigned char key)
{
if (!t)
return make_node(key);
if (t->item > key) /* insert to left subtree */
t->l = insert(t->l, key);
else /* if (t->item <= key), insert to right subtree */
t->r = insert(t->r, key);
return t;
}
link delete(link t, unsigned char key)
{
link p;
if (!t)
return NULL;
if (t->item > key) /* delete from left subtree */
t->l = delete(t->l, key);
else if (t->item < key) /* delete from right subtree */
t->r = delete(t->r, key);
else { /* if (t->item == key) */
if (t->l == NULL && t->r == NULL) { /* if t is leaf node */
free_node(t);
t = NULL;
} else if (t->l) { /* if t has left subtree */
/* replace t with the rightmost node in left subtree */
for (p = t->l; p->r; p = p->r);
t->item = p->item;
t->l = delete(t->l, t->item);
} else { /* if t has right subtree */
/* replace t with the leftmost node in right subtree */
for (p = t->r; p->l; p = p->l);
t->item = p->item;
t->r = delete(t->r, t->item);
}
}
return t;
}
void print_tree(link t)
{
if (t) {
printf("(");
printf("%d", t->item);
print_tree(t->l);
print_tree(t->r);
printf(")");
} else
printf("()");
}/* main.c */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "bst.h"
#define RANGE 100
#define N 6
void print_item(link p)
{
printf("%d", p->item);
}
int main()
{
int i, key;
link root = NULL;
srand(time(NULL));
for (i = 0; i < N; i++)
root = insert(root, rand() % RANGE);
printf("\t\\tree");
print_tree(root);
printf("\n\n");
while (root) {
key = rand() % RANGE;
if (search(root, key)) {
printf("delete %d in tree\n", key);
root = delete(root, key);
printf("\t\\tree");
print_tree(root);
printf("\n\n");
}
}
}$ ./a.out \tree(83(77(15()(35()()))())(86()(93()()))) delete 86 in tree \tree(83(77(15()(35()()))())(93()())) delete 35 in tree \tree(83(77(15()())())(93()())) delete 93 in tree \tree(83(77(15()())())()) delete 15 in tree \tree(83(77()())()) delete 83 in tree \tree(77()()) delete 77 in tree \tree()
程序的運行結果可以用Greg Lee編寫的The Tree Preprocessor(http://www.essex.ac.uk/linguistics/clmt/latex4ling/trees/tree/)轉換成樹形:
$ ./a.out | ./tree/tree
83
___|___
| |
77 86
_|__ _|__
| | | |
15 93
_|__ _|__
| | | |
35
_|__
| |
delete 86 in tree
83
___|___
| |
77 93
_|__ _|__
| | | |
15
_|__
| |
35
_|__
| |
delete 35 in tree
83
___|___
| |
77 93
_|__ _|__
| | | |
15
_|__
| |
delete 93 in tree
83
_|__
| |
77
_|__
| |
15
_|__
| |
delete 15 in tree
83
_|__
| |
77
_|__
| |
delete 83 in tree
77
_|__
| |
delete 77 in tree