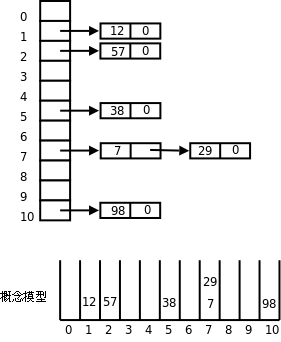
下圖示意了哈希表(Hash Table)這種資料結構。
如上圖所示,首先分配一個指針數組,數組的每個元素是一個鏈表的頭指針,每個鏈表稱為一個槽(Slot)。哪個數據應該放入哪個槽中由哈希函數決定,在這個例子中我們簡單地選取哈希函數h(x) = x % 11,這樣任意數據x都可以映射成0~10之間的一個數,就是槽的編號,將數據放入某個槽的操作就是鏈表的插入操作。
如果每個槽裡至多只有一個數據,可以想像這種情況下search、insert和delete操作的時間複雜度都是O(1),但有時會有多個數據被哈希函數映射到同一個槽中,這稱為碰撞(Collision),設計一個好的哈希函數可以把數據比較均勻地分佈到各個槽中,儘量避免碰撞。如果能把n個數據比較均勻地分佈到m個槽中,每個糟里約有n/m個數據,則search、insert和delete和操作的時間複雜度都是O(n/m),如果n和m的比是常數,則時間複雜度仍然是O(1)。一般來說,要處理的數據越多,構造哈希表時分配的槽也應該越多,所以n和m成正比這個假設是成立的。
請讀者自己編寫程序構造這樣一個哈希表,並實現search、insert和delete操作。
如果用我們學過的各種資料結構來表示n個數據的集合,下表是search、insert和delete操作在平均情況下的時間複雜度比較。
表 26.1. 各種資料結構的search、insert和delete操作在平均情況下的時間複雜度比較
| 資料結構 | search | insert | delete |
|---|---|---|---|
| 數組 | O(n),有序數組折半查找是O(lgn) | O(n) | O(n) |
| 雙向鏈表 | O(n) | O(1) | O(1) |
| 排序二叉樹 | O(lgn) | O(lgn) | O(lgn) |
| 哈希表(n與槽數m成正比) | O(1) | O(1) | O(1) |
1、統計一個文本檔案中每個單詞的出現次數,然後按出現次數排序並打印輸出。單詞由連續的英文字母組成,不區分大小寫。
2、實現一個函數求兩個數組的交集:size_t intersect(const int a[], size_t nmema, const int b[], size_t nmemb, int c[], size_t nmemc);。數組元素是32位int型的。數組a有nmema個元素且各不相同,數組b有nmemb個元素且各不相同。要求找出數組a和數組b的交集保存到數組c中,nmemc是數組c的最大長度,返回值表示交集中實際有多少個元素,如果交集中實際的元素數量超過了nmemc則返回nmemc個元素。數組a和數組b的元素數量可能會很大(比如上百萬個),需要設計儘可能快的算法。