2.2 數據抽象
譯者:飛龍
由於我們希望在程序中表達世界中的大量事物,我們發現它們的大多數都具有複合結構。日期是年月日,地理位置是精度和緯度。為了表示位置,我們希望程序語言具有將精度和緯度“粘合”為一對數據的能力 -- 也就是一個複合數據結構 -- 使我們的程序能夠以一種方式操作數據,將位置看做單個概念單元,它擁有兩個部分。
複合數據的使用也讓我們增加程序的模塊性。如果我們可以直接將地理位置看做對象來操作,我們就可以將程序的各個部分分離,它們根據這些值如何表示來從本質上處理這些值。將某個部分從程序中分離的一般技巧是一種叫做數據抽象的強大的設計方法論。這個部分用於處理數據表示,而程序用於操作數據。數據抽象使程序更易於設計、維護和修改。
數據抽象的特徵類似於函數抽象。當我們創建函數抽象時,函數如何實現的細節被隱藏了,而且特定的函數本身可以被任何具有相同行為的函數替換。換句話說,我們可以構造抽象來使函數的使用方式和函數的實現細節分離。與之相似,數據抽象是一種方法論,使我們將複合數據對象的使用細節與它的構造方式隔離。
數據抽象的基本概念是構造操作抽象數據的程序。也就是說,我們的程序應該以一種方式來使用數據,對數據做出儘可能少的假設。同時,需要定義具體的數據表示,獨立於使用數據的程序。我們系統中這兩部分的接口是一系列函數,叫做選擇器和構造器,它們基於具體表示實現了抽象數據。為了演示這個技巧,我們需要考慮如何設計一系列函數來操作有理數。
當你閱讀下一節時,要記住當今編寫的多數 Python 代碼使用了非常高級的抽象數據類型,它們內建於語言中,比如類、字典和列表。由於我們正在瞭解這些抽象的工作原理,我們自己不能使用它們。所以,我們會編寫一些不那麼 Python 化的代碼 -- 它並不是在語言中實現我們的概念的通常方式。但是,我們所編寫的代碼出於教育目的,它展示了這些抽象如何構建。要記住計算機科學並不只是學習如何使用編程語言,也學習它們的工作原理。
2.2.1 示例:有理數的算術
有理數可表示為整數的比值,並且它組成了實數的一個重要子類。類似於1/3或者17/29的有理數通常可編寫為:
<numerator>/<denominator>
其中,<numerator>和<denominator>都是值為整數的佔位符。有理數的值需要兩部分來描述。
有理數在計算機科學中很重要,因為它們就像整數那樣,可以準確表示。無理數(比如pi 或者 e 或者 sqrt(2))會使用有限的二元展開代替為近似值。所以在原則上,有理數的處理應該讓我們避免算術中的近似誤差。
但是,一旦我們真正將分子與分母相除,我們就會只剩下截斷的小數近似值:
>>> 1/3
0.3333333333333333
當我們開始執行測試時,這個近似值的問題就會出現:
>>> 1/3 == 0.333333333333333300000 # Beware of approximations
True
計算機如何將實數近似為定長的小數擴展,是另一門課的話題。這裡的重要概念是,通過將有理數表示為整數的比值,我們能夠完全避免近似問題。所以出於精確,我們希望將分子和分母分離,但是將它們看做一個單元。
我們從函數抽象中瞭解到,我們可以在瞭解某些部分的實現之前開始編出東西來。讓我們一開始假設我們已經擁有一種從分子和分母中構造有理數的方式。我們也假設,給定一個有理數,我們都有辦法來提取(或選中)它的分子和分母。讓我們進一步假設,構造器和選擇器以下面三個函數來提供:
make_rat(n, d)返回分子為n和分母為d的有理數。numer(x)返回有理數x的分子。denom(x)返回有理數x的分母。
我們在這裡正在使用一個強大的合成策略:心想事成。我們並沒有說有理數如何表示,或者numer、denom和make_rat如何實現。即使這樣,如果我們擁有了這三個函數,我們就可以執行加法、乘法,以及測試有理數的相等性,通過調用它們:
>>> def add_rat(x, y):
nx, dx = numer(x), denom(x)
ny, dy = numer(y), denom(y)
return make_rat(nx * dy + ny * dx, dx * dy)
>>> def mul_rat(x, y):
return make_rat(numer(x) * numer(y), denom(x) * denom(y))
>>> def eq_rat(x, y):
return numer(x) * denom(y) == numer(y) * denom(x)
現在我們擁有了由選擇器函數numer和denom,以及構造器函數make_rat定義的有理數操作。但是我們還沒有定義這些函數。我們需要以某種方式來將分子和分母粘合為一個單元。
2.2.2 元組
為了實現我們的數據抽象的具體層面,Python 提供了一種複合數據結構叫做tuple,它可以由逗號分隔的值來構造。雖然並不是嚴格要求,圓括號通常在元組周圍。
>>> (1, 2)
(1, 2)
元組的元素可以由兩種方式解構。第一種是我們熟悉的多重賦值:
>>> pair = (1, 2)
>>> pair
(1, 2)
>>> x, y = pair
>>> x
1
>>> y
2
實際上,多重賦值的本質是創建和解構元組。
訪問元組元素的第二種方式是通過下標運算符,寫作方括號:
>>> pair[0]
1
>>> pair[1]
2
Python 中的元組(以及多數其它編程語言中的序列)下標都以 0 開始,也就是說,下標 0 表示第一個元素,下標 1 表示第二個元素,以此類推。我們對這個下標慣例的直覺是,下標表示一個元素距離元組開頭有多遠。
與元素選擇操作等價的函數叫做__getitem__,它也使用位置在元組中選擇元素,位置的下標以 0 開始。
>>> from operator import getitem
>>> getitem(pair, 0)
1
元素是原始類型,也就是說 Python 的內建運算符可以操作它們。我們不久之後再來看元素的完整特性。現在,我們只對元組如何作為膠水來實現抽象數據類型感興趣。
**表示有理數。**元素提供了一個自然的方式來將有理數實現為一對整數:分子和分母。我們可以通過操作二元組來實現我們的有理數構造器和選擇器函數。
>>> def make_rat(n, d):
return (n, d)
>>> def numer(x):
return getitem(x, 0)
>>> def denom(x):
return getitem(x, 1)
用於打印有理數的函數完成了我們對抽象數據結構的實現。
>>> def str_rat(x):
"""Return a string 'n/d' for numerator n and denominator d."""
return '{0}/{1}'.format(numer(x), denom(x))
將它與我們之前定義的算術運算放在一起,我們可以使用我們定義的函數來操作有理數了。
>>> half = make_rat(1, 2)
>>> str_rat(half)
'1/2'
>>> third = make_rat(1, 3)
>>> str_rat(mul_rat(half, third))
'1/6'
>>> str_rat(add_rat(third, third))
'6/9'
就像最後的例子所展示的那樣,我們的有理數實現並沒有將有理數化為最簡。我們可以通過修改make_rat來補救。如果我們擁有用於計算兩個整數的最大公約數的函數,我們可以在構造一對整數之前將分子和分母化為最簡。這可以使用許多實用工具,例如 Python 庫中的現存函數。
>>> from fractions import gcd
>>> def make_rat(n, d):
g = gcd(n, d)
return (n//g, d//g)
雙斜槓運算符//表示整數除法,它會向下取整除法結果的小數部分。由於我們知道g能整除n和d,整數除法正好適用於這裡。現在我們的
>>> str_rat(add_rat(third, third))
'2/3'
符合要求。這個修改只通過修改構造器來完成,並沒有修改任何實現實際算術運算的函數。
**擴展閱讀。**上面的str_rat實現使用了格式化字符串,它包含了值的佔位符。如何使用格式化字符串和format方法的細節請見 Dive Into Python 3 的格式化字符串一節。
2.2.3 抽象界限
在以更多複合數據和數據抽象的例子繼續之前,讓我們思考一些由有理數示例產生的問題。我們使用構造器make_rat和選擇器numer和denom定義了操作。通常,數據抽象的底層概念是,基於某個值的類型的操作如何表達,為這個值的類型確定一組基本的操作。之後使用這些操作來操作數據。
我們可以將有理數系統想象為一系列層級。
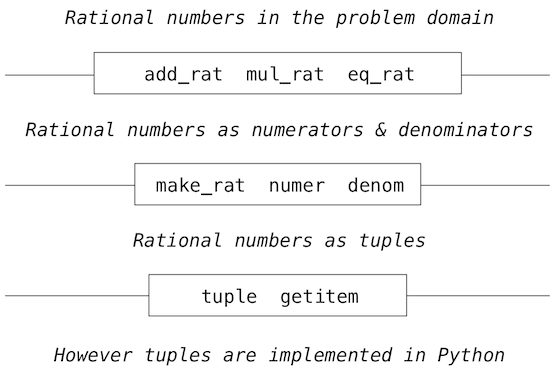
平行線表示隔離系統不同層級的界限。每一層上,界限分離了使用數據抽象的函數(上面)和實現數據抽象的函數(下面)。使用有理數的程序僅僅通過算術函數來操作它們:add_rat、mul_rat和eq_rat。相應地,這些函數僅僅由構造器和選擇器make_rat、numer和and denom來實現,它們本身由元組實現。元組如何實現的字節和其它層級沒有關係,只要元組支持選擇器和構造器的實現。
每一層上,盒子中的函數強制劃分了抽象的邊界,因為它們僅僅依賴於上層的表現(通過使用)和底層的實現(通過定義)。這樣,抽象界限可以表現為一系列函數。
抽象界限具有許多好處。一個好處就是,它們使程序更易於維護和修改。很少的函數依賴於特定的表現,當一個人希望修改表現時,不需要做很多修改。
2.2.4 數據屬性
我們通過實現算術運算來開始實現有理數,實現為這三個非特定函數:make_rat、numer和denom。這裡,我們可以認為已經定義了數據對象 -- 分子、分母和有理數 -- 上的運算,它們的行為由這三個函數規定。
但是數據意味著什麼?我們還不能說“提供的選擇器和構造器實現了任何東西”。我們需要保證這些函數一起規定了正確的行為。也就是說,如果我們從整數n和d中構造了有理數x,那麼numer(x)/denom(x)應該等於n/d。
通常,我們可以將抽象數據類型當做一些選擇器和構造器的集合,並帶有一些行為條件。只要滿足了行為條件(比如上面的除法特性),這些函數就組成了數據類型的有效表示。
這個觀點可以用在其他數據類型上,例如我們為實現有理數而使用的二元組。我們實際上不會談論元組是什麼,而是談論由語言提供的,用於操作和創建元組的運算符。我們現在可以描述二元組的行為條件,二元組通常叫做偶對,在表示有理數的問題中有所涉及。
為了實現有理數,我們需要一種兩個整數的粘合形式,它具有下列行為:
- 如果一個偶對
p由x和y構造,那麼getitem_pair(p, 0)返回x,getitem_pair(p, 1)返回y。
我們可以實現make_pair和getitem_pair,它們和元組一樣滿足這個描述:
>>> def make_pair(x, y):
"""Return a function that behaves like a pair."""
def dispatch(m):
if m == 0:
return x
elif m == 1:
return y
return dispatch
>>> def getitem_pair(p, i):
"""Return the element at index i of pair p."""
return p(i)
使用這個實現,我們可以創建和操作偶對:
>>> p = make_pair(1, 2)
>>> getitem_pair(p, 0)
1
>>> getitem_pair(p, 1)
2
這個函數的用法不同於任何直觀上的,數據應該是什麼的概念。而且,這些函數滿足於在我們的程序中表示覆合數據。
需要注意的微妙的一點是,由make_pair返回的值是叫做dispatch的函數,它接受參數m並返回x或y。之後,getitem_pair調用了這個函數來獲取合適的值。我們在這一章中會多次返回這個調度函數的話題。
這個偶對的函數表示並不是 Python 實際的工作機制(元組實現得更直接,出於性能因素),但是它可以以這種方式工作。這個函數表示雖然不是很明顯,但是是一種足夠完美來表示偶對的方式,因為它滿足了偶對唯一需要滿足的條件。這個例子也表明,將函數當做值來操作的能力,提供給我們表示複合數據的能力。