4. 隊列與廣度優先搜索

4. 隊列與廣度優先搜索
上一頁	第 12 章棧與隊列	下一頁

隊列也是一組元素的集合，也提供兩種基本操作：Enqueue（入隊）將元素添加到隊尾，Dequeue（出隊）從隊頭取出元素並返回。就像排隊買票一樣，先來先服務，先入隊的人也是先出隊的，這種方式稱為FIFO（First In First Out，先進先出），有時候隊列本身也被稱為FIFO。

下面我們用隊列解決迷宮問題。程序如下：

例 12.4. 用廣度優先搜索解迷宮問題

#include <stdio.h>

#define MAX_ROW 5
#define MAX_COL 5

struct point { int row, col, predecessor; } queue[512];
int head = 0, tail = 0;

void enqueue(struct point p)
{
	queue[tail++] = p;
}

struct point dequeue(void)
{
	return queue[head++];
}

int is_empty(void)
{
	return head == tail;
}

int maze[MAX_ROW][MAX_COL] = {
	0, 1, 0, 0, 0,
	0, 1, 0, 1, 0,
	0, 0, 0, 0, 0,
	0, 1, 1, 1, 0,
	0, 0, 0, 1, 0,
};

void print_maze(void)
{
	int i, j;
	for (i = 0; i < MAX_ROW; i++) {
		for (j = 0; j < MAX_COL; j++)
			printf("%d ", maze[i][j]);
		putchar('\n');
	}
	printf("*********\n");
}

void visit(int row, int col)
{
	struct point visit_point = { row, col, head-1 };
	maze[row][col] = 2;
	enqueue(visit_point);
}

int main(void)
{
	struct point p = { 0, 0, -1 };

	maze[p.row][p.col] = 2;
	enqueue(p);
	
	while (!is_empty()) {
		p = dequeue();
		if (p.row == MAX_ROW - 1  /* goal */
		    && p.col == MAX_COL - 1)
			break;
		if (p.col+1 < MAX_COL     /* right */
		    && maze[p.row][p.col+1] == 0)
			visit(p.row, p.col+1);
		if (p.row+1 < MAX_ROW     /* down */
		    && maze[p.row+1][p.col] == 0)
			visit(p.row+1, p.col);
		if (p.col-1 >= 0          /* left */
		    && maze[p.row][p.col-1] == 0)
			visit(p.row, p.col-1);
		if (p.row-1 >= 0          /* up */
		    && maze[p.row-1][p.col] == 0)
			visit(p.row-1, p.col);
		print_maze();
	}
	if (p.row == MAX_ROW - 1 && p.col == MAX_COL - 1) {
		printf("(%d, %d)\n", p.row, p.col);
		while (p.predecessor != -1) {
			p = queue[p.predecessor];
			printf("(%d, %d)\n", p.row, p.col);
		}
	} else
		printf("No path!\n");

	return 0;
}

運行結果如下：

其實仍然可以像例 12.3 “用深度優先搜索解迷宮問題”一樣用predecessor數組表示每個點的前趨，但我想換一種更方便的資料結構，直接在每個點的結構體中加一個成員表示前趨：

struct point { int row, col, predecessor; } queue[512];
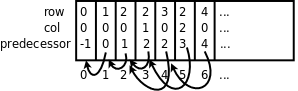
int head = 0, tail = 0;

變數head和tail是隊頭和隊尾指針，head總是指向隊頭，tail總是指向隊尾的下一個元素。每個點的predecessor成員也是一個指針，指向它的前趨在queue數組中的位置。如下圖所示：

圖 12.3. 廣度優先搜索的隊列資料結構

為了幫助理解，我把這個算法改寫成偽代碼如下：

將起點標記為已走過併入隊;
while (隊列非空) {
	出隊一個點p;
	if (p這個點是終點)
		break;
	否則沿右、下、左、上四個方向探索相鄰的點
	if (和p相鄰的點有路可走，並且還沒走過)
		將相鄰的點標記為已走過併入隊，它的前趨就是剛出隊的p點;
}
if (p點是終點) {
	打印p點的座標;
	while (p點有前趨) {
		p點 = p點的前趨;
		打印p點的座標;
	}
} else
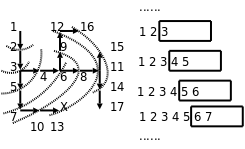
	沒有路線可以到達終點;

從打印的搜索過程可以看出，這個算法的特點是沿各個方向同時展開搜索，每個可以走通的方向輪流往前走一步，這稱為廣度優先搜索（BFS，Breadth First Search）。探索迷宮和隊列變化的過程如下圖所示。

圖 12.4. 廣度優先搜索

廣度優先是一種步步為營的策略，每次都從各個方向探索一步，將前線推進一步，圖中的虛線就表示這個前線，隊列中的元素總是由前線的點組成的，可見正是隊列先進先出的性質使這個算法具有了廣度優先的特點。廣度優先搜索還有一個特點是可以找到從起點到終點的最短路徑，而深度優先搜索找到的不一定是最短路徑，比較本節和上一節程序的運行結果可以看出這一點，想一想為什麼。

習題

1、本節的例子直接在隊列元素中加一個指針成員表示前趨，想一想為什麼上一節的例 12.3 “用深度優先搜索解迷宮問題”不能採用這種方法表示前趨？

2、本節例子中給隊列分配的存儲空間是512個元素，其實沒必要這麼多，那麼解決這個問題至少要分配多少個元素的隊列空間呢？跟什麼因素有關？

上一頁	上一級	下一頁
3. 深度優先搜索	起始頁	5. 環形隊列