插入排序算法採取增量式（Incremental）的策略解決問題，每次添一個元素到已排序的子序列中，逐漸將整個數組排序完畢，它的時間複雜度是O(n²)。下面介紹另一種典型的排序算法－－歸併排序，它採取分而治之（Divide-and-Conquer）的策略，時間複雜度是Θ(nlgn)。歸併排序的步驟如下：

在描述歸併排序的步驟時又調用了歸併排序本身，可見這是一個遞歸的過程。

#include <stdio.h>

#define LEN 8
int a[LEN] = { 5, 2, 4, 7, 1, 3, 2, 6 };

void merge(int start, int mid, int end)
{
	int n1 = mid - start + 1;
	int n2 = end - mid;
	int left[n1], right[n2];
	int i, j, k;

	for (i = 0; i < n1; i++) /* left holds a[start..mid] */
		left[i] = a[start+i];
	for (j = 0; j < n2; j++) /* right holds a[mid+1..end] */
		right[j] = a[mid+1+j];

	i = j = 0;
	k = start;
	while (i < n1 && j < n2)
		if (left[i] < right[j])
			a[k++] = left[i++];
		else
			a[k++] = right[j++];

	while (i < n1) /* left[] is not exhausted */
		a[k++] = left[i++];
	while (j < n2) /* right[] is not exhausted */
		a[k++] = right[j++];
}

void sort(int start, int end)
{
	int mid;
	if (start < end) {
		mid = (start + end) / 2;
		printf("sort (%d-%d, %d-%d) %d %d %d %d %d %d %d %d\n", 
		       start, mid, mid+1, end, 
		       a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7]);
		sort(start, mid);
		sort(mid+1, end);
		merge(start, mid, end);
		printf("merge (%d-%d, %d-%d) to %d %d %d %d %d %d %d %d\n", 
		       start, mid, mid+1, end, 
		       a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7]);
	}
}

int main(void)
{
	sort(0, LEN-1);
	return 0;
}

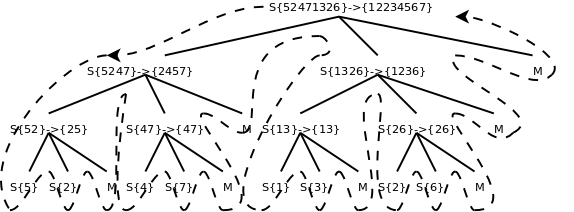
sort (0-3, 4-7) 5 2 4 7 1 3 2 6
sort (0-1, 2-3) 5 2 4 7 1 3 2 6
sort (0-0, 1-1) 5 2 4 7 1 3 2 6
merge (0-0, 1-1) to 2 5 4 7 1 3 2 6
sort (2-2, 3-3) 2 5 4 7 1 3 2 6
merge (2-2, 3-3) to 2 5 4 7 1 3 2 6
merge 0-1, 2-3) to 2 4 5 7 1 3 2 6
sort (4-5, 6-7) 2 4 5 7 1 3 2 6
sort (4-4, 5-5) 2 4 5 7 1 3 2 6
merge (4-4, 5-5) to 2 4 5 7 1 3 2 6
sort (6-6, 7-7) 2 4 5 7 1 3 2 6
merge (6-6, 7-7) to 2 4 5 7 1 3 2 6
merge (4-5, 6-7) to 2 4 5 7 1 2 3 6
merge (0-3, 4-7) to 1 2 2 3 4 5 6 7

sort函數把a[start..end]平均分成兩個子序列，分別是a[start..mid]和a[mid+1..end]，對這兩個子序列分別遞歸調用sort函數進行排序，然後調用merge函數將排好序的兩個子序列合併起來，由於兩個子序列都已經排好序了，合併的過程很簡單，每次循環取兩個子序列中最小的元素進行比較，將較小的元素取出放到最終的排序序列中，如果其中一個子序列的元素已取完，就把另一個子序列剩下的元素都放到最終的排序序列中。為了便於理解程序，我在sort函數開頭和結尾插了打印語句，可以看出調用過程是這樣的：

圖 11.4. 歸併排序調用過程

圖中S表示sort函數，M表示merge函數，整個控制流程沿虛線所示的方向調用和返回。由於sort函數遞歸調用了自己兩次，所以各函數之間的調用關係呈樹狀結構。畫這個圖只是為了清楚地展現歸併排序的過程，讀者在理解遞歸函數時一定不要全部展開來看，而是要抓住Base Case和遞推關係來理解。我們分析一下歸併排序的時間複雜度，以下分析出自[算法導論]。

首先分析merge函數的時間複雜度。在merge函數中演示了C99的新特性－－可變長數組，當然也可以避免使用這一特性，比如把left和right都按最大長度LEN分配。不管用哪種辦法，定義數組並分配存儲空間的執行時間都可以看作常數，與數組的長度無關，常數用Θ-notation記作Θ(1)。設子序列a[start..mid]的長度為n1，子序列[mid+1..end]的長度為n2，a[start..end]的總長度為n=n1+n2，則前兩個for循環的執行時間是Θ(n1+n2)，也就是Θ(n)，後面三個for循環合在一起看，每走一次循環就會在最終的排序序列中確定一個元素，最終的排序序列共有n個元素，所以執行時間也是Θ(n)。兩個Θ(n)再加上若干常數項，merge函數總的執行時間仍是Θ(n)，其中n=end-start+1。

然後分析sort函數的時間複雜度，當輸入長度n=1，也就是start==end時，if條件不成立，執行時間為常數Θ(1)，當輸入長度n>1時：

設輸入長度為n的sort函數的執行時間為T(n)，綜上所述：

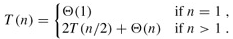
這是一個遞推公式（Recurrence），我們需要消去等號右側的T(n)，把T(n)寫成n的函數。其實符合一定條件的Recurrence的展開有數學公式可以套，這裡我們略去嚴格的數學證明，只是從直觀上看一下這個遞推公式的結果。當n=1時可以設T(1)=c₁，當n>1時可以設T(n)=2T(n/2)+c₂n，我們取c₁和c₂中較大的一個設為c，把原來的公式改為：

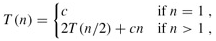
這樣計算出的結果應該是T(n)的上界。下面我們把T(n/2)展開成2T(n/4)+cn/2（下圖中的(c)），然後再把T(n/4)進一步展開，直到最後全部變成T(1)=c（下圖中的(d)）：

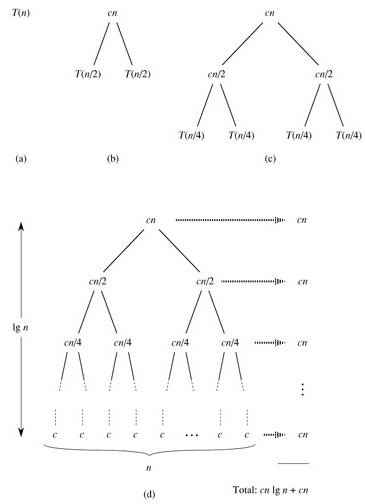
把圖(d)中所有的項加起來就是總的執行時間。這是一個樹狀結構，每一層的和都是cn，共有lgn+1層，因此總的執行時間是cnlgn+cn，相比nlgn來說，cn項可以忽略，因此T(n)的上界是Θ(nlgn)。

如果先前取c₁和c₂中較小的一個設為c，計算出的結果應該是T(n)的下界，然而推導過程一樣，結果也是Θ(nlgn)。既然T(n)的上下界都是Θ(nlgn)，顯然T(n)就是Θ(nlgn)。

和插入排序的平均情況相比歸併排序更快一些，雖然merge函數的步驟較多，引入了較大的常數、係數和低次項，但是對於較大的輸入長度n，這些都不是主要因素，歸併排序的時間複雜度是Θ(nlgn)，而插入排序的平均情況是Θ(n²)，這就決定了歸併排序是更快的算法。但是不是任何情況下歸併排序都優於插入排序呢？哪些情況適用插入排序而不適用歸併排序？留給讀者思考。

int partition(int start, int end)
{
	從a[start..end]中選取一個pivot元素（比如選a[start]為pivot）;
	在一個循環中移動a[start..end]的數據，將a[start..end]分成兩半，
	使a[start..mid-1]比pivot元素小，a[mid+1..end]比pivot元素大，而a[mid]就是pivot元素;
	return mid;
}

void quicksort(int start, int end)
{
	int mid;
	if (end > start) {
		mid = partition(start, end);
		quicksort(start, mid-1);
		quicksort(mid+1, end);
	}
}