解決同一個問題可以有很多種算法,比較評價算法的好壞,一個重要的標準就是算法的時間複雜度。現在研究一下插入排序算法的執行時間,按照習慣,輸入長度LEN以下用n表示。設循環中各條語句的執行時間分別是c1、c2、c3、c4、c5這樣五個常數[23]:
void insertion_sort(void) 執行時間
{
int i, j, key;
for (j = 1; j < LEN; j++) {
key = a[j]; c1
i = j - 1; c2
while (i >= 0 && a[i] > key) {
a[i+1] = a[i]; c3
i--; c4
}
a[i+1] = key; c5
}
}顯然外層for循環的執行次數是n-1次,假設內層的while循環執行m次,則總的執行時間粗略估計是(n-1)*(c1+c2+c5+m*(c3+c4))。當然,for和while後面()括號中的賦值和條件判斷的執行也需要時間,而我沒有設一個常數來表示,這不影響我們的粗略估計。
這裡有一個問題,m不是個常數,也不取決於輸入長度n,而是取決於具體的輸入數據。在最好情況下,數組a的原始數據已經排好序了,while循環一次也不執行,總的執行時間是(c1+c2+c5)*n-(c1+c2+c5),可以表示成an+b的形式,是n的線性函數(Linear Function)。那麼在最壞情況(Worst Case)下又如何呢?所謂最壞情況是指數組a的原始數據正好是從大到小排好序的,請讀者想一想為什麼這是最壞情況,然後把上式中的m替換掉算一下執行時間是多少。
數組a的原始數據屬於最好和最壞情況的都比較少見,如果原始數據是隨機的,可稱為平均情況(Average Case)。如果原始數據是隨機的,那麼每次循環將已排序的子序列a[1..j-1]與新插入的元素key相比較,子序列中平均都有一半的元素比key大而另一半比key小,請讀者把上式中的m替換掉算一下執行時間是多少。最後的結論應該是:在最壞情況和平均情況下,總的執行時間都可以表示成an2+bn+c的形式,是n的二次函數(Quadratic Function)。
在分析算法的時間複雜度時,我們更關心最壞情況而不是最好情況,理由如下:
最壞情況給出了算法執行時間的上界,我們可以確信,無論給什麼輸入,算法的執行時間都不會超過這個上界,這樣為比較和分析提供了便利。
對於某些算法,最壞情況是最常發生的情況,例如在資料庫中查找某個信息的算法,最壞情況就是資料庫中根本不存在該信息,都找遍了也沒有,而某些應用場合經常要查找一個信息在資料庫中存在不存在。
雖然最壞情況是一種悲觀估計,但是對於很多問題,平均情況和最壞情況的時間複雜度差不多,比如插入排序這個例子,平均情況和最壞情況的時間複雜度都是輸入長度n的二次函數。
比較兩個多項式a1n+b1和a2n2+b2n+c2的值(n取正整數)可以得出結論:n的最高次指數是最主要的決定因素,常數項、低次冪項和係數都是次要的。比如100n+1和n2+1,雖然後者的係數小,當n較小時前者的值較大,但是當n>100時,後者的值就遠遠大於前者了。如果同一個問題可以用兩種算法解決,其中一種算法的時間複雜度為線性函數,另一種算法的時間複雜度為二次函數,當問題的輸入長度n足夠大時,前者明顯優於後者。因此我們可以用一種更粗略的方式表示算法的時間複雜度,把係數和低次冪項都省去,線性函數記作Θ(n),二次函數記作Θ(n2)。
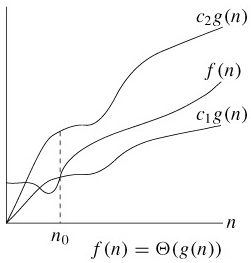
Θ(g(n))表示和g(n)同一量級的一類函數,例如所有的二次函數f(n)都和g(n)=n2屬於同一量級,都可以用Θ(n2)來表示,甚至有些不是二次函數的也和n2屬於同一量級,例如2n2+3lgn。“同一量級”這個概念可以用下圖來說明(該圖出自[算法導論]):
如果可以找到兩個正的常數c1和c2,使得n足夠大的時候(也就是n≥n0的時候)f(n)總是夾在c1g(n)和c2g(n)之間,就說f(n)和g(n)是同一量級的,f(n)就可以用Θ(g(n))來表示。
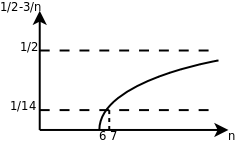
以二次函數為例,比如1/2n2-3n,要證明它是屬於Θ(n2)這個集合的,我們必須確定c1、c2和n0,這些常數不隨n改變,並且當n≥n0以後,c1n2≤1/2n2-3n≤c2n2總是成立的。為此我們從不等式的每一邊都除以n2,得到c1≤1/2-3/n≤c2。見下圖:
這樣就很容易看出來,無論n取多少,該函數一定小於1/2,因此c2=1/2,當n=6時函數值為0,n>6時該函數都大於0,可以取n0=7,c1=1/14,這樣當n≥n0時都有1/2-3/n≥c1。通過這個證明過程可以得出結論,當n足夠大時任何an2+bn+c都夾在c1n2和c2n2之間,相對於n2項來說bn+c的影響可以忽略,a可以通過選取合適的c1、c2來補償。
幾種常見的時間複雜度函數按數量級從小到大的順序依次是:Θ(lgn),Θ(sqrt(n)),Θ(n),Θ(nlgn),Θ(n2),Θ(n3),Θ(2n),Θ(n!)。其中,lgn通常表示以10為底n的對數,但是對於Θ-notation來說,Θ(lgn)和Θ(log2n)並無區別(想一想這是為什麼),在算法分析中lgn通常表示以2為底n的對數。可是什麼算法的時間複雜度裡會出現lgn呢?回顧插入排序的時間複雜度分析,無非是循環體的執行時間乘以循環次數,只有加和乘運算,怎麼會出來lg呢?下一節歸併排序的時間複雜度裡面就有lg,請讀者留心lg運算是從哪出來的。
除了Θ-notation之外,表示算法的時間複雜度常用的還有一種Big-O notation。我們知道插入排序在最壞情況和平均情況下時間複雜度是Θ(n2),在最好情況下是Θ(n),數量級比Θ(n2)要小,那麼總結起來在各種情況下插入排序的時間複雜度是O(n2)。Θ的含義和“等於”類似,而大O的含義和“小於等於”類似。