如果定義一個概念需要用到這個概念本身，我們稱它的定義是遞歸的（Recursive）。例如：

這只是一個玩笑，如果你在字典上看到這麼一個詞條肯定要怒了。然而數學上確實有很多概念是用它自己來定義的，比如n的階乘（Factorial）是這樣定義的：n的階乘等於n乘以n-1的階乘。如果這樣就算定義完了，恐怕跟上面那個詞條有異曲同工之妙了：n-1的階乘是什麼？是n-1乘以n-2的階乘。那n-2的階乘又是什麼？這樣下去永遠也沒完。因此需要定義一個最關鍵的基礎條件（Base Case）：0的階乘等於1。

因此，3!=3*2!，2!=2*1!，1!=1*0!=1*1=1，正因為有了Base Case，才不會永遠沒完地數下去，知道了1!=1我們再反過來算回去，2!=2*1!=2*1=2，3!=3*2!=3*2=6。下面用程序來完成這一計算過程，我們要寫一個計算階乘的函數factorial，先把Base Case這種最簡單的情況寫進去：

int factorial(int n)
{
	if (n == 0)
		return 1;
}

如果參數n不是0應該return什麼呢？根據定義，應該return n*factorial(n-1);，為了下面的分析方便，我們引入幾個臨時變數把這個語句拆分一下：

int factorial(int n)
{
	if (n == 0)
		return 1;
	else {
		int recurse = factorial(n-1);
		int result = n * recurse;
		return result;
	}
}

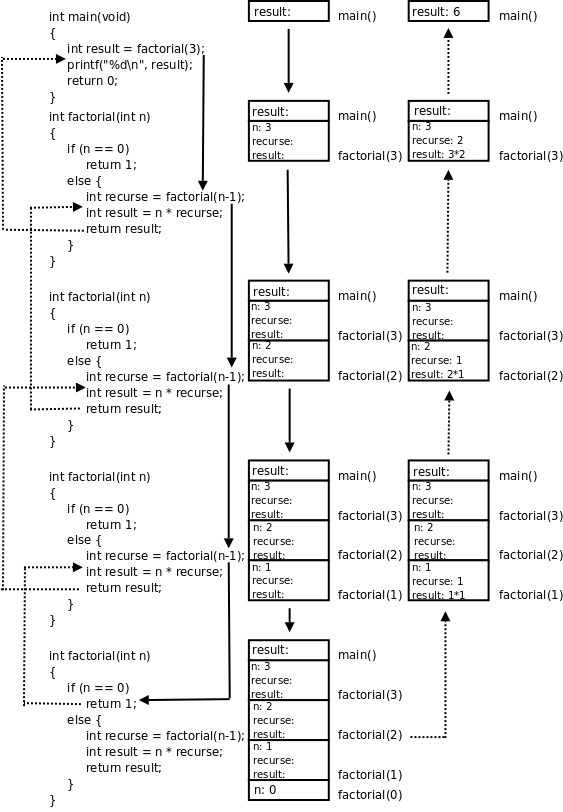
factorial這個函數居然可以自己調用自己？是的。自己直接或間接調用自己的函數稱為遞歸函數。這裡的factorial是直接調用自己，有些時候函數A調用函數B，函數B又調用函數A，也就是函數A間接調用自己，這也是遞歸函數。如果你覺得迷惑，可以把factorial(n-1)這一步看成是在調用另一個函數－－另一個有着相同函數名和相同代碼的函數，調用它就是跳到它的代碼裡執行，然後再返回factorial(n-1)這個調用的下一步繼續執行。我們以factorial(3)為例分析整個調用過程，如下圖所示：

圖 5.2. factorial(3)的調用過程

圖中用實線箭頭表示調用，用虛線箭頭表示返回，右側的框表示在調用和返回過程中各層函數調用的存儲空間變化情況。

我們看上圖右側存儲空間的變化過程，隨着函數調用的層層深入，存儲空間的一端逐漸增長，然後隨着函數調用的層層返回，存儲空間的這一端又逐漸縮短，並且每次訪問參數和局部變數時只能訪問這一端的存儲單元，而不能訪問內部的存儲單元，比如當factorial(2)的存儲空間位於末端時，只能訪問它的參數和局部變數，而不能訪問factorial(3)和main()的參數和局部變數。具有這種性質的資料結構稱為堆棧或棧（Stack），隨着函數調用和返回而不斷變化的這一端稱為棧頂，每個函數調用的參數和局部變數的存儲空間（上圖的每個小方框）稱為一個棧幀（Stack Frame）。操作系統為程序的運行預留了一塊棧空間，函數調用時就在這個棧空間裡分配棧幀，函數返回時就釋放棧幀。

在寫一個遞歸函數時，你如何證明它是正確的？像上面那樣跟蹤函數的調用和返回過程算是一種辦法，但只是factorial(3)就已經這麼麻煩了，如果是factorial(100)呢？雖然我們已經證明了factorial(3)是正確的，因為它跟我們用數學公式計算的過程一樣，結果也一樣，但這不能代替factorial(100)的證明，你怎麼辦？別的函數你可以跟蹤它的調用過程去證明它的正確性，因為每個函數隻調用一次就返回了，但是對於遞歸函數，這麼跟下去只會跟得你頭都大了。事實上並不是每個函數調用都需要鑽進去看的。我們在調用printf時沒有鑽進去看它是怎麼打印的，我們只是相信它能打印，能正確完成它的工作，然後就繼續寫下面的代碼了。在上一節中，我們寫了distance和area函數，然後立刻測試證明了這兩個函數是正確的，然後我們寫area_point時調用了這兩個函數：

return area(distance(x1, y1, x2, y2));

在寫這一句的時候，我們需要鑽進distance和area函數中去走一趟才知道我們調用得是否正確嗎？不需要，因為我們已經相信這兩個函數能正確工作了，也就是相信把座標傳給distance它就能返回正確的距離，把半徑傳給area它就能返回正確的面積，因此調用它們去完成另外一件工作也應該是正確的。這種“相信”稱為Leap of Faith，首先相信一些結論，然後再用它們去證明另外一些結論。

在寫factorial(n)的代碼時寫到這個地方：

...
int recurse = factorial(n-1);
int result = n * recurse;
...

這時，如果我們相信factorial(n-1)是正確的，也就是相信傳給它n-1它就能返回(n-1)!，那麼recurse就是(n-1)!，那麼result就是n*(n-1)!，也就是n!，這正是我們要返回的factorial(n)的結果。當然這有點奇怪：我們還沒寫完factorial這個函數，憑什麼要相信factorial(n-1)是正確的？可Leap of Faith本身就是Leap（跳躍）的，不是嗎？如果你相信你正在寫的遞歸函數是正確的，並調用它，然後在此基礎上寫完這個遞歸函數，那麼它就會是正確的，從而值得你相信它正確。

這麼說好像有點兒玄，我們從數學上嚴格證明一下factorial函數的正確性。剛纔說了，factorial(n)的正確性依賴于factorial(n-1)的正確性，只要後者正確，在後者的結果上乘個n返回這一步顯然也沒有疑問，那麼我們的函數實現就是正確的。因此要證明factorial(n)的正確性就是要證明factorial(n-1)的正確性，同理，要證明factorial(n-1)的正確性就是要證明factorial(n-2)的正確性，依此類推下去，最後是：要證明factorial(1)的正確性就是要證明factorial(0)的正確性。而factorial(0)的正確性不依賴于別的函數調用，它就是程序中的一個小的分支return 1;，這個1是我們根據階乘的定義寫的，肯定是正確的，因此factorial(1)的實現是正確的，因此factorial(2)也正確，依此類推，最後factorial(n)也是正確的。其實這就是在中學時學的數學歸納法（Mathematical Induction），用數學歸納法來證明只需要證明兩點：Base Case正確，遞推關係正確。寫遞歸函數時一定要記得寫Base Case，否則即使遞推關係正確，整個函數也不正確。如果factorial函數漏掉了Base Case：

int factorial(int n)
{
	int recurse = factorial(n-1);
	int result = n * recurse;
	return result;
}

那麼這個函數就會永遠調用下去，直到操作系統為程序預留的棧空間耗盡程序崩潰（段錯誤）為止，這稱為無窮遞歸（Infinite recursion）。

到目前為止我們只學習了全部C語法的一個小的子集，但是現在應該告訴你：這個子集是完備的，它本身就可以作為一門編程語言了，以後還要學習很多C語言特性，但全部都可以用已經學過的這些特性來代替。也就是說，以後要學的C語言特性會使代碼寫起來更加方便，但不是必不可少的，現在學的這些已經完全覆蓋了第 1 節 “程序和編程語言”講的五種基本指令了。有的讀者會說循環還沒講到呢，是的，循環在下一章才講，但有一個重要的結論就是遞歸和循環是等價的，用循環能做的事用遞歸都能做，反之亦然，事實上有的編程語言（比如某些LISP實現）只有遞歸而沒有循環。計算機指令能做的所有事情就是數據存取、運算、測試和分支、循環（或遞歸），在計算機上運行高級語言寫的程序最終也要翻譯成指令，指令做不到的事情高級語言寫的程序肯定也做不到，雖然高級語言有豐富的語法特性，但也只是比指令寫起來更方便而已，能做的事情是一樣多的。那麼，為什麼計算機要設計成這樣？在設計時怎麼想到計算機應該具備這幾樣功能，而不是更多或更少的功能？這些要歸功于早期的計算機科學家，例如Alan Turing，他們在計算機還沒有誕生的年代就從數學理論上為計算機的設計指明了方向。有興趣的讀者可以參考有關計算理論的教材，例如[IATLC]。

遞歸絶不只是為解決一些奇技淫巧的數學題^[8]而想出來的招，它是計算機的精髓所在，也是編程語言的精髓所在。我們學習在C的語法時已經看到很多遞歸定義了，例如在第 1 節 “數學函數”講過的語法規則中，“表達式”就是遞歸定義的：

再比如在第 1 節 “if語句”講過的語規則中，“語句”也是遞歸定義的：

可見編譯器在解析我們寫的程序時一定也用了大量的遞歸，有關編譯器的實現原理可參考[Dragon Book]。