目前為止你看到了很多示例代碼，也在它們的基礎上做了很多改動並在這個過程中鞏固所學的知識。但是如果從頭開始編寫一個程序解決某個問題，應該按什麼步驟來寫呢？本節提出一種增量式（Incremental）開發的思路，很適合初學者。

現在問題來了：我們要編一個程序求圓的面積，圓的半徑以兩個端點的座標(x₁, y₁)和(x₂, y₂)給出。首先分析和分解問題，把大問題分解成小問題，再對小問題分別求解。這個問題可分為兩步：

首先編寫distance這個函數，我們已經明確了它的參數是兩點的座標，返回值是兩點間距離，可以先寫一個簡單的函數定義：

double distance(double x1, double y1, double x2, double y2)
{
	return 0.0;
}

初學者寫到這裡就已經不太自信了：這個函數定義寫得對嗎？雖然我是按我理解的語法規則寫的，但書上沒有和這個一模一樣的例子，萬一不小心遺漏了什麼呢？既然不自信就不要再往下寫了，沒有一個平穩的心態來寫程序很可能會引入Bug。所以在函數定義中插一個return 0.0立刻結束掉它，然後立刻測試這個函數定義得有沒有錯：

int main(void)
{
	printf("distance is %f\n", distance(1.0, 2.0, 4.0, 6.0));
	return 0;
}

編譯，運行，一切正常。這時你就會建立起信心了：既然沒問題，就不用管它了，繼續往下寫。在測試時給這個函數的參數是(1.0, 2.0)和(4.0, 6.0)，兩點的x座標距離是3.0，y座標距離是4.0，因此兩點間距離應該是5.0，你必須事先知道正確答案是5.0，這樣你才能測試程序計算的結果對不對。當然，現在函數還沒實現，計算結果肯定是不對的。現在我們再往函數里添一點代碼：

double distance(double x1, double y1, double x2, double y2)
{
	double dx = x2 - x1;
	double dy = y2 - y1;
	printf("dx is %f\ndy is %f\n", dx, dy);

	return 0.0;
}

如果你不確定dx和dy這樣初始化行不行，那麼就此打住，在函數里插一條打印語句把dx和dy的值打出來看看。把它和上面的main函數一起編譯運行，由於我們事先知道結果應該是3.0和4.0，因此能夠驗證程序算得對不對。一旦驗證無誤，函數里的這句打印就可以撤掉了，像這種打印語句，以及我們用來測試的main函數，都起到了類似腳手架（Scaffold）的作用：在蓋房子時很有用，但它不是房子的一部分，房子蓋好之後就可以拆掉了。房子蓋好之後可能還需要維修、加蓋、翻新，又要再加上腳手架，這很麻煩，要是當初不用拆就好了，可是不拆不行，不拆多難看啊。寫代碼卻可以有一個更高明的解決辦法：把Scaffolding的代碼註釋掉。

double distance(double x1, double y1, double x2, double y2)
{
	double dx = x2 - x1;
	double dy = y2 - y1;
	/* printf("dx is %f\ndy is %f\n", dx, dy); */
	return 0.0;
}

這樣如果以後出了新的Bug又需要跟蹤調試時，還可以把這句重新加進代碼中使用。兩點的x座標距離和y座標距離都沒問題了，下面求它們的平方和：

double distance(double x1, double y1, double x2, double y2)
{
	double dx = x2 - x1;
	double dy = y2 - y1;
	double dsquared = dx * dx + dy * dy;
	printf("dsquared is %f\n", dsquared);

	return 0.0;
}

然後再編譯、運行，看看是不是得25.0。這樣的增量式開發非常適合初學者，每寫一行代碼都編譯運行，確保沒問題了再寫一下行，一方面在寫代碼時更有信心，另一方面也方便了調試：總是有一個先前的正確版本做參照，改動之後如果出了問題，几乎可以肯定就是剛纔改的那行代碼出的問題，這樣就避免了必須從很多行代碼中查找分析到底是哪一行出的問題。在這個過程中printf功不可沒，你懷疑哪一行代碼有問題，就插一個printf進去看看中間的計算結果，任何錯誤都可以通過這個辦法找出來。以後我們會介紹程序調試工具gdb，它提供了更強大的調試功能幫你分析更隱蔽的錯誤。但即使有了gdb，printf這個最原始的辦法仍然是最直接、最有效的。最後一步，我們完成這個函數：

#include <math.h>
#include <stdio.h>

double distance(double x1, double y1, double x2, double y2)
{
	double dx = x2 - x1;
	double dy = y2 - y1;
	double dsquared = dx * dx + dy * dy;
	double result = sqrt(dsquared);

	return result;
}

int main(void)
{
	printf("distance is %f\n", distance(1.0, 2.0, 4.0, 6.0));
	return 0;
}

然後編譯運行，看看是不是得5.0。隨着編程經驗越來越豐富，你可能每次寫若干行代碼再一起測試，而不是像現在這樣每寫一行就測試一次，但不管怎麼樣，增量式開發的思路是很有用的，它可以幫你節省大量的調試時間，不管你有多強，都不應該一口氣寫完整個程序再編譯運行，那几乎是一定會有Bug的，到那時候再找Bug就難了。

這個程序中引入了很多臨時變數：dx、dy、dsquared、result，如果你有信心把整個表達式一次性寫好，也可以不用臨時變數：

double distance(double x1, double y1, double x2, double y2)
{
	return sqrt((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1));
}

這樣寫簡潔得多了。但如果寫錯了呢？只知道是這一長串表達式有錯，根本不知道錯在哪，而且整個函數就一個語句，插printf都沒地方插。所以用臨時變數有它的好處，使程序更清晰，調試更方便，而且有時候可以避免不必要的計算，例如上面這一行表達式要把(x2-x1)計算兩遍，如果算完(x2-x1)把結果存在一個臨時變數dx裡，就不需要再算第二遍了。

接下來編寫area這個函數：

double area(double radius)
{
	return 3.1416 * radius * radius;
}

給出兩點的座標求距離，給出半徑求圓的面積，這兩個子問題都解決了，如何把它們組合起來解決整個問題呢？給出半徑的兩端點座標(1.0, 2.0)和(4.0, 6.0)求圓的面積，先用distance函數求出半徑的長度，再把這個長度傳給area函數：

double radius = distance(1.0, 2.0, 4.0, 6.0);
double result = area(radius);

也可以這樣：

double result = area(distance(1.0, 2.0, 4.0, 6.0));

我們一直把“給出半徑的兩端點座標求圓的面積”這個問題當作整個問題來看，如果它也是一個更大的程序當中的子問題呢？我們可以把先前的兩個函數組合起來做成一個新的函數以便日後使用：

double area_point(double x1, double y1, double x2, double y2)
{
	return area(distance(x1, y1, x2, y2));
}

還有另一種組合的思路，不是把distance和area兩個函數調用組合起來，而是把那兩個函數中的語句組合到一起：

double area_point(double x1, double y1, double x2, double y2)
{
	double dx = x2 - x1;
	double dy = y2 - y1;
	double radius = sqrt(dx * dx + dy * dy);

	return 3.1416 * radius * radius;
}

這樣組合是不理想的。這樣組合了之後，原來寫的distance和area兩個函數還要不要了呢？如果不要了刪掉，那麼如果有些情況只需要求兩點間的距離，或者只需要給定半徑長度求圓的面積呢？area_point把所有語句都寫在一起，太不靈活了，滿足不了這樣的需要。如果保留distance和area同時也保留這個area_point怎麼樣呢？area_point和distance有相同的代碼，一旦在distance函數中發現了Bug，或者要升級distance這個函數採用更高的計算精度，那麼不僅要修改distance，還要記着修改area_point，同理，要修改area也要記着修改area_point，維護重複的代碼是非常容易出錯的，在任何時候都要儘量避免。因此，儘可能復用（Reuse）以前寫的代碼，避免寫重複的代碼。封裝就是為了復用，把解決各種小問題的代碼封裝成函數，在解決第一個大問題時可以用這些函數，在解決第二個大問題時可以復用這些函數。

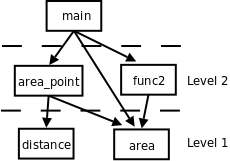
解決問題的過程是把大的問題分成小的問題，小的問題再分成更小的問題，這個過程在代碼中的體現就是函數的分層設計（Stratify）。distance和area是兩個底層函數，解決一些很小的問題，而area_point是一個上層函數，上層函數通過調用底層函數來解決更大的問題，底層和上層函數都可以被更上一層的函數調用，最終所有的函數都直接或間接地被main函數調用。如下圖所示：

圖 5.1. 函數的分層設計