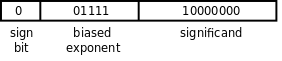
浮點數在計算機中的表示是基于科學計數法（Scientific Notation）的，我們知道32767這個數用科學計數法可以寫成3.2767×10⁴，3.2767稱為尾數（Mantissa，或者叫Significand），4稱為指數（Exponent）。浮點數在計算機中的表示與此類似，只不過基數（Radix）是2而不是10。下面我們用一個簡單的模型來解釋浮點數的基本概念。我們的模型由三部分組成：符號位、指數部分（表示2的多少次方）和尾數部分（小數點前面是0，尾數部分只表示小數點後的數字）。

圖 14.6. 一種浮點數格式

如果要表示17這個數，我們知道17=17.0×10⁰=0.17×10²，類似地，17=(10001)₂×2⁰=(0.10001)₂×2⁵，把尾數的有效數字全部移到小數點後，這樣就可以表示為：

圖 14.7. 17的浮點數表示

如果我們要表示0.25就遇到新的困難了，因為0.25=1×2^-2=(0.1)₂×2^-1，而我們的模型中指數部分沒有規定如何表示負數。我們可以在指數部分規定一個符號位，然而更廣泛採用的辦法是使用偏移的指數（Biased Exponent）。規定一個偏移值，比如16，實際的指數要加上這個偏移值再填寫到指數部分，這樣比16大的就表示正指數，比16小的就表示負指數。要表示0.25，指數部分應該填16-1=15：

圖 14.8. 0.25的偏移指數浮點數表示

現在還有一個問題需要解決：每個浮點數的表示都不唯一，例如17=(0.10001)₂×2⁵=(0.010001)₂×2⁶，這樣給計算機處理增加了複雜性。為瞭解決這個問題，我們規定尾數部分的最高位必須是1，也就是說尾數必須以0.1開頭，對指數做相應的調整，這稱為正規化（Normalize）。由於尾數部分的最高位必須是1，這個1就不必保存了，可以節省出一位來用於提高精度，我們說最高位的1是隱含的（Implied）。這樣17就只有一種表示方法了，指數部分應該是16+5=21=(10101)₂，尾數部分去掉最高位的1是0001：

圖 14.9. 17的正規化尾數浮點數表示

兩個浮點數相加，首先把小數點對齊然後相加：

圖 14.10. 浮點數相加

由於浮點數表示的精度有限，計算結果末尾的10兩位被捨去了。做浮點運算時要注意精度損失（Significance Loss）問題，有時計算順序不同也會導致不同的結果，比如11.0010000+0.00000001+0.00000001=11.0010000+0.00000001=11.0010000，後面加的兩個很小的數全被捨去了，沒有對計算結果產生任何影響，但如果調一下計算順序它們就能影響到計算結果了，0.00000001+0.00000001+11.0010000=0.00000010+11.0010000=11.0010001。再比如128.25=(10000000.01)₂，需要10個有效位，而我們的模型中尾數部分是8位，算上隱含的最高位1一共有9個有效位，那麼128.25的浮點數表示只能捨去末尾的1，表示成(10000000.0)₂，其實跟128相等了。在第 2 節 “if/else語句”講過浮點數不能做精確比較，現在讀者應該知道為什麼不能精確比較了。

整數運算會產生溢出，浮點運算也會產生溢出，浮點運算的溢出也分上溢和下溢兩種，但和整數運算的定義不同。假設整數採用8位2's Complement表示法，取值範圍是-128~127，如果計算結果是-130則稱為下溢，計算結果是130則稱為上溢。假設按本節介紹的浮點數表示法，取值範圍是-(0.111111111)₂×2¹⁵~(0.111111111)₂×2¹⁵，如果計算結果超出這個範圍則稱為上溢；如果計算結果未超出這個範圍但絶對值太小了，在-(0.1)₂×2^-16~(0.1)₂×2^-16之間，那麼也同樣無法表示，稱為下溢。

浮點數是一個相當複雜的話題，不同平台的浮點數表示和浮點運算也有較大差異，本節只是通過這個簡單的模型介紹一些基本概念而不深入討論，理解了這些基本概念有助於你理解浮點數標準，目前業界廣泛採用的符點數標準是由IEEE（Institute of Electrical and Electronics Engineers）制定的IEEE 754。

最後討論一個細節問題。我們知道，定義全局變數時如果沒有Initializer就用0初始化，定義數組時如果Initializer中提供的元素不夠那麼剩下的元素也用0初始化。例如：

int i;
double d;
double a[10] = { 1.0 };

“用0初始化”的意思是變數i、變數d和數組元素a[1]~a[9]的所有位元組都用0填充，或者說所有bit都是0。無論是用Sign and Magnitude表示法、1's Complement表示法還是2's Complement表示法，一個整數的所有bit是0都表示0值，但一個浮點數的所有bit是0一定表示0值嗎？嚴格來說不一定，某種平台可能會規定一個浮點數的所有bit是0並不表示0值，但[C99 Rationale]第6.7.8節的條款25提到：As far as the committee knows, all machines treat all bits zero as a representation of floating-point zero. But, all bits zero might not be the canonical representation of zero. 因此在絶大多數平台上，一個浮點數的所有bit是0就表示0值。